相关文章:
- 李航《统计学习方法》第二章——用Python实现感知器模型(MNIST数据集)
- 李航《统计学习方法》第三章——用Python实现KNN算法(MNIST数据集)
- 李航《统计学习方法》第四章——用Python实现朴素贝叶斯分类器(MNIST数据集)
- 李航《统计学习方法》第五章——用Python实现决策树(MNIST数据集)
- 李航《统计学习方法》第六章——用Python实现逻辑斯谛回归(MNIST数据集)
- 李航《统计学习方法》第六章——用Python实现最大熵模型(MNIST数据集)
- 李航《统计学习方法》第七章——用Python实现支持向量机模型(伪造数据集)>
- 李航《统计学习方法》第八章——用Python+Cpp实现AdaBoost算法(MNIST数据集)
隐马尔科夫模型有3个基本问题:
1. 概率计算问题(前向算法,后向算法)
2. 学习问题 (Baum-Welch算法)
3. 预测问题 (维特比算法)
我实现了Baum-Welch算法,且该算法也包含了前向算法与后向算法。
Baum-Welch算法
这里先贴上书中的算法

数据集
本来打算试一下用自己写的HMM跑一下中文分词,但很可惜,代码运行的比较慢。
所以改成 模拟 三角波 以及 正弦波
代码
代码已放到Github上,这边也贴出来
# encoding=utf8
import numpy as np
import csv
class HMM(object):
def __init__(self,N,M):
self.A = np.zeros((N,N)) # 状态转移概率矩阵
self.B = np.zeros((N,M)) # 观测概率矩阵
self.Pi = np.array([1.0/N]*N) # 初始状态概率矩阵
self.N = N # 可能的状态数
self.M = M # 可能的观测数
def cal_probality(self, O):
self.T = len(O)
self.O = O
self.forward()
return sum(self.alpha[self.T-1])
def forward(self):
"""
前向算法
"""
self.alpha = np.zeros((self.T,self.N))
# 公式 10.15
for i in range(self.N):
self.alpha[0][i] = self.Pi[i]*self.B[i][self.O[0]]
# 公式10.16
for t in range(1,self.T):
for i in range(self.N):
sum = 0
for j in range(self.N):
sum += self.alpha[t-1][j]*self.A[j][i]
self.alpha[t][i] = sum * self.B[i][self.O[t]]
def backward(self):
"""
后向算法
"""
self.beta = np.zeros((self.T,self.N))
# 公式10.19
for i in range(self.N):
self.beta[self.T-1][i] = 1
# 公式10.20
for t in range(self.T-2,-1,-1):
for i in range(self.N):
for j in range(self.N):
self.beta[t][i] += self.A[i][j]*self.B[j][self.O[t+1]]*self.beta[t+1][j]
def cal_gamma(self, i, t):
"""
公式 10.24
"""
numerator = self.alpha[t][i]*self.beta[t][i]
denominator = 0
for j in range(self.N):
denominator += self.alpha[t][j]*self.beta[t][j]
return numerator/denominator
def cal_ksi(self, i, j, t):
"""
公式 10.26
"""
numerator = self.alpha[t][i]*self.A[i][j]*self.B[j][self.O[t+1]]*self.beta[t+1][j]
denominator = 0
for i in range(self.N):
for j in range(self.N):
denominator += self.alpha[t][i]*self.A[i][j]*self.B[j][self.O[t+1]]*self.beta[t+1][j]
return numerator/denominator
def init(self):
"""
随机生成 A,B,Pi
并保证每行相加等于 1
"""
import random
for i in range(self.N):
randomlist = [random.randint(0,100) for t in range(self.N)]
Sum = sum(randomlist)
for j in range(self.N):
self.A[i][j] = randomlist[j]/Sum
for i in range(self.N):
randomlist = [random.randint(0,100) for t in range(self.M)]
Sum = sum(randomlist)
for j in range(self.M):
self.B[i][j] = randomlist[j]/Sum
def train(self, O, MaxSteps = 100):
self.T = len(O)
self.O = O
# 初始化
self.init()
step = 0
# 递推
while step<MaxSteps:
step+=1
print(step)
tmp_A = np.zeros((self.N,self.N))
tmp_B = np.zeros((self.N,self.M))
tmp_pi = np.array([0.0]*self.N)
self.forward()
self.backward()
# a_{ij}
for i in range(self.N):
for j in range(self.N):
numerator=0.0
denominator=0.0
for t in range(self.T-1):
numerator += self.cal_ksi(i,j,t)
denominator += self.cal_gamma(i,t)
tmp_A[i][j] = numerator/denominator
# b_{jk}
for j in range(self.N):
for k in range(self.M):
numerator = 0.0
denominator = 0.0
for t in range(self.T):
if k == self.O[t]:
numerator += self.cal_gamma(j,t)
denominator += self.cal_gamma(j,t)
tmp_B[j][k] = numerator / denominator
# pi_i
for i in range(self.N):
tmp_pi[i] = self.cal_gamma(i,0)
self.A = tmp_A
self.B = tmp_B
self.Pi = tmp_pi
def generate(self, length):
import random
I = []
# start
ran = random.randint(0,1000)/1000.0
i = 0
while self.Pi[i]<ran or self.Pi[i]<0.0001:
ran -= self.Pi[i]
i += 1
I.append(i)
# 生成状态序列
for i in range(1,length):
last = I[-1]
ran = random.randint(0, 1000) / 1000.0
i = 0
while self.A[last][i] < ran or self.A[last][i]<0.0001:
ran -= self.A[last][i]
i += 1
I.append(i)
# 生成观测序列
Y = []
for i in range(length):
k = 0
ran = random.randint(0, 1000) / 1000.0
while self.B[I[i]][k] < ran or self.B[I[i]][k]<0.0001:
ran -= self.B[I[i]][k]
k += 1
Y.append(k)
return Y
def triangle(length):
'''
三角波
'''
X = [i for i in range(length)]
Y = []
for x in X:
x = x % 6
if x <= 3:
Y.append(x)
else:
Y.append(6-x)
return X,Y
def show_data(x,y):
import matplotlib.pyplot as plt
plt.plot(x, y, 'g')
plt.show()
return y
if __name__ == '__main__':
hmm = HMM(10,4)
tri_x, tri_y = triangle(20)
hmm.train(tri_y)
y = hmm.generate(100)
print(y)
x = [i for i in range(100)]
show_data(x,y)
运行结果
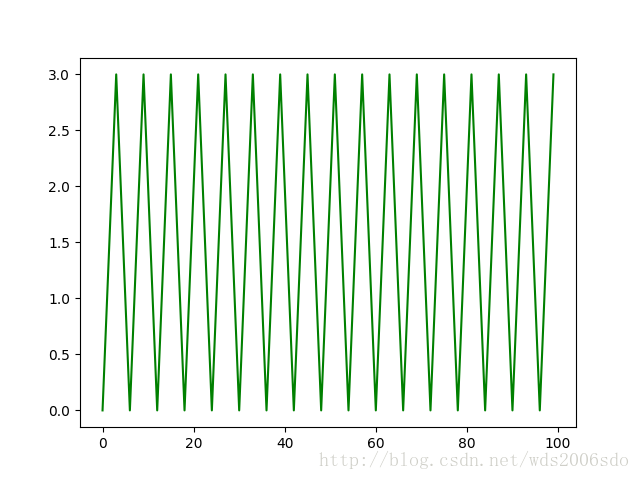
三角波
三角波比较简单,我设置N=10,扔进去长度为20的序列,训练100次,下图是其生成的长度为100的序列。
可以看出效果还是很不错的。
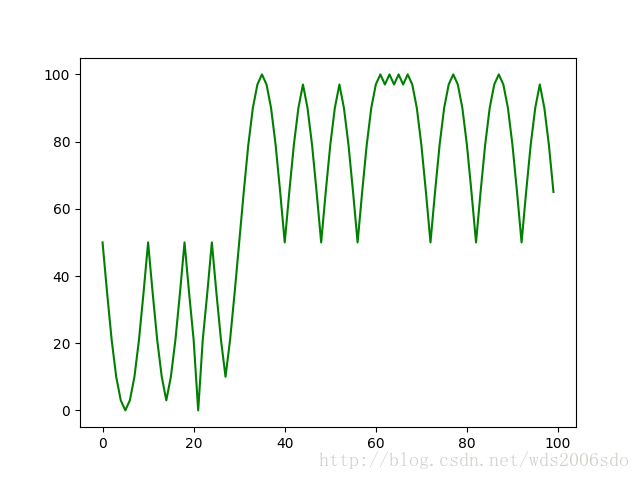
正弦波
正弦波有些麻烦,因为观测序列不能太大,所以我设置N=15,M=100,扔进去长度为40的序列,训练100次,训练的非常慢,下图是其生成的长度为100的序列。
可以看出效果一般,如果改成C的代码,并增加N应该是能模拟的。
balabala
隐马尔科夫模型的初值真的非常重要,我曾尝试过每行平均和单位矩阵两种方式,结果100轮迭代后啥都没变,所以最好还是随机初始化。
还有几点细节不是很理解
1. 如果有多个序列如何同时训练?
2. 训练如何停止?我现在的做法是设置一个训练次数上限。








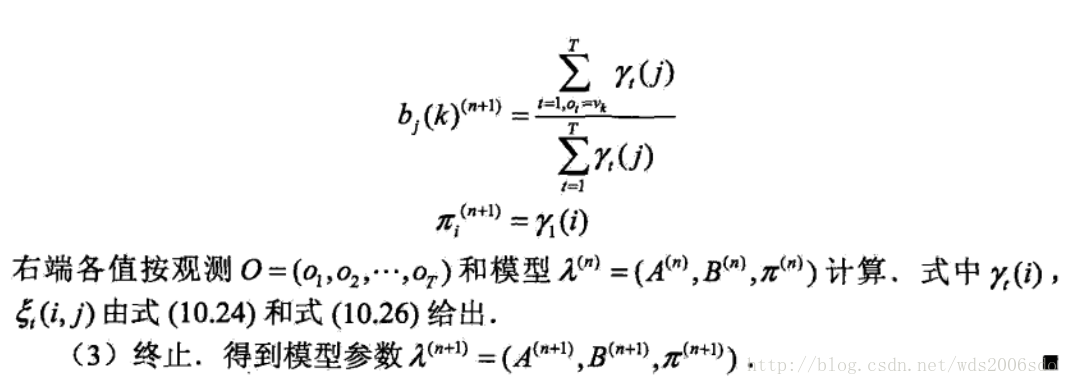














 93
93

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








