本文的主要参考资料是张小飞老师的《阵列信号处理及MATLAB实现(第3版)》(电子工业出版社出版)。
背景
近场方向到达(Direction of Arrival, DOA)估计是阵列信号处理领域的一个重要研究课题。DOA估计可以分为远场DOA估计和近场DOA估计。在近场DOA估计中,由于信号源距离阵列较近,因此信号的波前会呈现出球面波特性,这与远场情况下的平面波假设不同。近场DOA估计在很多实际应用中都非常重要,例如,无线通信、雷达、声纳、地震学以及生物医学等领域。
近场信号和远场信号有以下特点:
- 近场与远场的区别:
- 近场区域:信号源到阵列的距离远小于阵列的孔径大小,波前是球面波。
- 远场区域:信号源到阵列的距离远大于阵列的孔径大小,波前可以近似为平面波。
- 近场DOA估计的挑战:
- 近场效应导致信号波前的复杂性增加。
- 需要精确估计信号源的距离和角度信息。
- 阵列校准和误差的影响更加敏感。
- 近场DOA估计算法:
- 基于子空间的方法:如Music算法、ESPRIT算法等,这些算法需要修改以适应近场条件。
- 基于最大似然的方法:考虑信号源距离的影响,通过最大化似然函数来估计DOA。
- 基于稀疏表示的方法:利用信号的稀疏性质,通过求解稀疏重构问题来估计DOA。
- 基于深度学习的方法:近年来,深度学习技术也被应用于DOA估计,通过训练神经网络来直接从数据中估计DOA。
近场信号模型
接下来介绍近场DOA估计中的二维MUSIC算法(2D-MUSIC),在信号模型中,采用均匀线阵ULA(Uniform Linear Array),所谓二维就是指2个待估计的参数,距离
r
r
r和到达角
θ
\theta
θ。信号模型图如下所示:

阵列天线由
M
=
2
N
+
1
M=2N+1
M=2N+1个传感器阵元组成,相邻阵元间的间距为
d
d
d,以中心标号为0的传感器阵元为中心阵元,左右两边各分布
N
N
N个单边阵元,左右两边阵元共享中心标号为0的传感器阵元。因此,阵元
m
∈
[
−
N
,
⋯
,
−
2
,
−
1
,
0
,
1
,
2
,
⋯
,
N
]
m\in[-N,\cdots,-2,-1,0,1,2,\cdots,N]
m∈[−N,⋯,−2,−1,0,1,2,⋯,N],并且假设有
K
K
K个窄带近场非相干信号入射,在上图信号模型中画出了第
k
(
1
,
2
,
.
.
.
,
K
)
k(1,2,...,K)
k(1,2,...,K)个近场信号入射,距离中心参考阵元距离
r
k
r_k
rk,到达角为
θ
k
\theta_k
θk。那么其接收信号矩阵
x
(
t
)
\boldsymbol{x}\left( t \right)
x(t)可以写成如下形式
x
(
t
)
=
[
x
−
N
(
t
)
,
⋯
,
x
−
1
(
t
)
,
x
0
(
t
)
,
x
1
(
t
)
,
⋯
,
x
N
(
t
)
]
T
=
[
a
(
θ
1
,
r
1
)
,
a
(
θ
2
,
r
2
)
,
⋯
,
a
(
θ
K
,
r
K
)
]
s
(
t
)
+
n
(
t
)
=
A
x
s
(
t
)
+
n
(
t
)
\boldsymbol{x}\left( t \right) =\left[ x_{-N}\left( t \right) ,\cdots ,x_{-1}\left( t \right) ,x_0\left( t \right) ,x_1\left( t \right) ,\cdots ,x_N\left( t \right) \right] ^T\\ =\left[ \boldsymbol{a}\left( \theta _1,r_1 \right) ,\boldsymbol{a}\left( \theta _2,r_2 \right) ,\cdots ,\boldsymbol{a}\left( \theta _K,r_K \right) \right] \boldsymbol{s}\left( t \right) +\boldsymbol{n}\left( t \right) \\ =\boldsymbol{A}_x\boldsymbol{s}\left( t \right) +\boldsymbol{n}\left( t \right)
x(t)=[x−N(t),⋯,x−1(t),x0(t),x1(t),⋯,xN(t)]T=[a(θ1,r1),a(θ2,r2),⋯,a(θK,rK)]s(t)+n(t)=Axs(t)+n(t)
其中,
A
x
\boldsymbol{A}_x
Ax是阵列流形,
s
(
t
)
\boldsymbol{s}\left( t \right)
s(t)是信号矩阵,
n
(
t
)
\boldsymbol{n}\left( t \right)
n(t)是加性高斯白噪声矩阵。
根据近场信号的菲涅尔近似,第
k
k
k个信号的导向矢量
a
(
θ
k
,
r
k
)
\boldsymbol{a}\left( \theta _k,r_k \right)
a(θk,rk)可以被写成
a
(
θ
k
,
r
k
)
=
[
e
j
(
γ
k
(
−
N
+
1
)
+
ϕ
k
(
−
N
+
1
)
2
)
,
.
.
.
,
e
j
(
γ
k
(
−
1
)
+
ϕ
k
(
−
1
)
2
)
,
1
,
e
j
(
γ
k
1
+
ϕ
k
1
2
)
,
.
.
.
,
e
j
(
γ
k
N
+
ϕ
k
N
2
)
]
T
a\left( \theta _k,r_k \right) =\left[ \text{e}^{\text{j}\left( \gamma _k\left( -N+1 \right) +\phi _k\left( -N+1 \right) ^2 \right)},...,\text{e}^{\text{j}\left( \gamma _k\left( -1 \right) +\phi _k\left( -1 \right) ^2 \right)},1,\text{e}^{\text{j}\left( \gamma _k1+\phi _k1^2 \right)},...,\text{e}^{\text{j}\left( \gamma _kN+\phi _kN^2 \right)} \right] ^{\text{T}}
a(θk,rk)=[ej(γk(−N+1)+ϕk(−N+1)2),...,ej(γk(−1)+ϕk(−1)2),1,ej(γk1+ϕk12),...,ej(γkN+ϕkN2)]T并且,
γ
k
=
−
2
π
d
λ
sin
θ
k
,
ϕ
k
=
π
d
2
λ
r
k
cos
2
θ
k
\gamma _k=-2\pi \frac{d}{\lambda}\sin \theta _k,\phi _k=\pi \frac{d^2}{\lambda r_k}\cos ^2\theta _k
γk=−2πλdsinθk,ϕk=πλrkd2cos2θk
2D-MUSIC
假设采样时间大于相干时间,有限次采样得到的接收信号的协方差矩阵可表示为如下所示,并对该协方差矩阵进行特征分解:
R
^
x
=
x
(
t
)
x
H
(
t
)
/
K
=
U
S
Σ
S
U
S
H
+
U
N
Σ
N
U
N
H
\hat{R}_x=x(t)x^{\mathrm{H}}(t)/K=\boldsymbol{U}_{\text{S}}\boldsymbol{\Sigma }_{\text{S}}\boldsymbol{U}_{\text{S}}^{\text{H}}+\boldsymbol{U}_{\text{N}}\boldsymbol{\Sigma }_{\text{N}}\boldsymbol{U}_{\text{N}}^{\text{H}}
R^x=x(t)xH(t)/K=USΣSUSH+UNΣNUNH
其中,
x
(
t
)
\boldsymbol{x}\left( t \right)
x(t)是接收信号矩阵,
K
K
K是快拍数。
(
∙
)
H
(\bullet)^{\mathrm{H}}
(∙)H是共轭转置,
U
S
\boldsymbol{U}_S
US是由大特征值对应的特征向量组成的信号子空间,
U
N
\boldsymbol{U}_N
UN是由小特征值对应的特征向量组成的噪声子空间。
根据子空间理论,在近场时,噪声子空间和信号子空间的正交性仍然成立,因此,基于远场的MUSIC方法在近场时仍然适用。
在搜索区间
r
∈
[
0.62
(
D
3
/
λ
)
1
/
2
,
(
2
D
2
/
λ
)
]
,
θ
∈
[
−
π
/
2
,
π
/
2
]
r\in[0.62(D^3/\lambda)^{1/2},(2D^2/\lambda)],\theta\in[-\pi/2,\pi/2]
r∈[0.62(D3/λ)1/2,(2D2/λ)],θ∈[−π/2,π/2]内构造谱峰搜器,
D
=
M
d
D=Md
D=Md。
P
(
θ
,
r
)
=
1
a
H
(
θ
,
r
)
U
n
U
n
H
a
(
θ
,
r
)
P\left( \theta ,r \right) =\frac{1}{a^H\left( \theta ,r \right) U_nU_{n}^{H}a\left( \theta ,r \right)}
P(θ,r)=aH(θ,r)UnUnHa(θ,r)1
其中,
a
(
θ
,
r
)
=
[
e
j
(
γ
(
−
N
)
+
ϕ
(
−
N
)
2
)
,
.
.
.
,
e
j
(
γ
(
−
1
)
+
ϕ
(
−
1
)
2
)
,
1
,
e
j
(
γ
1
+
ϕ
1
2
)
,
.
.
.
,
e
j
(
γ
N
+
ϕ
N
2
)
]
T
a\left( \theta ,r \right) =\left[ \text{e}^{\text{j}\left( \gamma \left( -N \right) +\phi \left( -N \right) ^2 \right)},...,\text{e}^{\text{j}\left( \gamma \left( -1 \right) +\phi \left( -1 \right) ^2 \right)},1,\text{e}^{\text{j}\left( \gamma 1+\phi 1^2 \right)},...,\text{e}^{\text{j}\left( \gamma N+\phi N^2 \right)} \right] ^{\text{T}}
a(θ,r)=[ej(γ(−N)+ϕ(−N)2),...,ej(γ(−1)+ϕ(−1)2),1,ej(γ1+ϕ12),...,ej(γN+ϕN2)]T并且,
γ
=
−
2
π
d
λ
sin
θ
,
ϕ
=
π
d
2
λ
r
cos
2
θ
\gamma =-2\pi \frac{d}{\lambda}\sin \theta ,\phi=\pi \frac{d^2}{\lambda r}\cos ^2\theta
γ=−2πλdsinθ,ϕ=πλrd2cos2θ。
得到对应峰值的下标,即目标对应的距离与角度:
θ
^
=
[
θ
^
1
,
θ
^
2
,
⋯
,
θ
^
K
]
r
^
=
[
r
^
1
,
r
^
2
,
⋯
,
r
^
K
]
\begin{aligned}&\hat{\theta}=[\hat{\theta}_{1},\hat{\theta}_{2},\cdots,\hat{\theta}_{K}]\\&\hat{r}=[\hat{r}_{1},\hat{r}_{2},\cdots,\hat{r}_{K}]\end{aligned}
θ^=[θ^1,θ^2,⋯,θ^K]r^=[r^1,r^2,⋯,r^K]
其中
θ
^
\hat{\theta}
θ^,
r
^
\hat{r}
r^分别是对应信号相对于参考阵元的距离和到达角度。
2D-MUSIC的算法流程可以表示如下:
Step1:根据采样得到的信号矩阵构造接收信号的协方差矩阵的估计值。
Step2:对接收信号的协方差矩阵进行特征值分解,然后按照特征值的大小顺序,把与信号个数相等的较大的特征值和对应的特征向量看成信号子空间,把剩下的对应部分看成噪声子空间
U
n
U_n
Un。
Step3:根据噪声特征向量和信号向量的正交性,构造空间谱峰搜索函数,对其进行谱峰搜索可以得到
K
K
K组配对的信源目标角度与距离参数的估计结果。
接下来利用2个近场非相干信号源进行仿真,其距离参考阵元的距离
r
k
r_k
rk和到达角
θ
k
\theta_k
θk分别为
(
20
°
,
1.85
λ
)
\left( 20°,1.85\lambda \right)
(20°,1.85λ)、
(
40
°
,
4.8
λ
)
\left( 40°,4.8\lambda \right)
(40°,4.8λ),阵元间距
d
=
λ
/
4
d=\lambda/4
d=λ/4,信噪比
S
N
R
=
20
d
B
SNR=20dB
SNR=20dB,单边阵元数
N
=
4
N=4
N=4,快拍数
K
=
2000
K=2000
K=2000。
matlab代码如下:
clc
clear all
close all
%%%%%%近场2D-MUSIC算法
derad = pi/180; %角度->弧度
M = 2; % 信源数目
lamta=1;% 信号波长
Nx =4; % 单边阵元个数
Mx=2*Nx+1; %总阵元个数
d =lamta/4; % 阵元间距
D = (Mx-1)*d; %阵列孔径
distance_left = 0.62*sqrt((D.^3)/lamta);%距离搜索的下界
distance_right = 2*(D.^2)/lamta;%距离搜索的上界
xita_k = [20 40].*derad; % x轴待估计角度
snr =20; % 信噪比
K =2000; % 快拍数
r_k=[1.85*lamta,4.8*lamta]; %信号源距离
m=-Nx:1:Nx;%x轴入射点位
gama_k=-2*pi*d.*sin(xita_k)./lamta;
gama_k=gama_k';
phi_k=pi*d*d.*cos(xita_k).*cos(xita_k)./(r_k.*lamta);
phi_k=phi_k';
A_x=exp(1i*(gama_k.*m+phi_k.*m.*m));%构造阵列流形矩阵
% %%%%%%构建信号模型%%%%%
S=randn(M,K);
X1=A_x'*S;
X1=awgn(X1,snr,'measured'); %将白色高斯噪声添加到信号中
Rxx= X1*X1'/K;%获取接收信号的协方差矩阵
% 特征值分解
[EV,D]=eig(Rxx); %特征值分解
EVA=diag(D)'; %将特征值矩阵对角线提取并转为一行
[EVA,I]=sort(EVA); %将特征值排序 从小到大
EV=fliplr(EV(:,I)); % 对应特征矢量排序
Un=EV(:,M+1:end);%获取x轴接收数据的噪声子空间
%进行角度和距离的二维搜索
num_distance=0;
for distance=0.01:0.01:distance_right
num_distance=num_distance+1;
for iang=1:360
angle(iang)=(iang-180)/2;
gama_k=-2*pi*d.*sind(angle(iang))./lamta;
gama_k=gama_k';
phi_k=pi*d*d.*cosd(angle(iang)).*cosd(angle(iang))./(distance.*lamta);
phi_k=phi_k';
A_x=exp(1i*(gama_k.*m+phi_k.*m.*m));
A_x=A_x';
P_search(num_distance,iang)=1/abs(A_x'*Un*Un'*A_x);
end
end
distance=0.01:0.01:distance_right;
angle(iang)=(iang-180)/2;
[distance,angle]=meshgrid(distance,angle);
%绘制三维图
mesh(distance',angle',P_search);
yticks([-90:10:90]);
ylabel('角度/°');
xticks([0:0.5:distance_right]);
xlabel('r/\lambda');
figure
contour(distance',angle',P_search)
yticks([-90:10:90]);
ylabel('角度/°');
xticks([0:0.5:distance_right]);
xlabel('r/\lambda');
画出相应的三维谱峰搜索图和二维等高线图,可以看出算法可以有效估计信源的角度和距离参数,且参数自动配对。
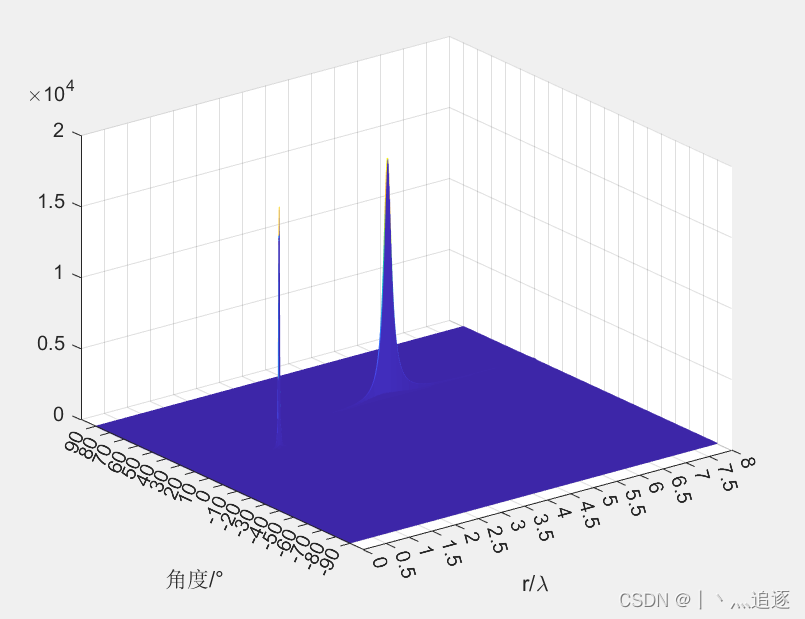









 本文介绍了近场信号与远场信号的区别,着重探讨了二维MUSIC算法在近场DOA估计中的应用,包括信号模型、协方差矩阵分析、特征分解和角度距离估计过程。通过Matlab仿真,展示了算法的有效性和信源参数的自动匹配性能。
本文介绍了近场信号与远场信号的区别,着重探讨了二维MUSIC算法在近场DOA估计中的应用,包括信号模型、协方差矩阵分析、特征分解和角度距离估计过程。通过Matlab仿真,展示了算法的有效性和信源参数的自动匹配性能。
















 1993
1993

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








