收敛准则（一）

我们知道，收敛数列必定有界，这是数列的有界性。也就是说，数列有界是数列收敛的必要条件，那么自然就会问：数列有界是不是数列收敛的充分条件呢。答案是否定的，也即有界数列不一定收敛。在这个系列，我们就研究一下关于有界数列与收敛的关系，主要回答以下两个问题：

1.有界数列加上什么条件可保证收敛？

2.有界数列不加其它条件，可得到什么弱一些的结论？

Part1

先回答第一个问题，直接给答案：

单调有界数列必定收敛

我们证明这个结论：

因此，我们得到进一步的结论：

单调有界数列必定收敛，其极限是以通项构成的数集的确界

下面举四个例子。

• 例1
  

观察数列的通项，可以知道，知道了x1，就能知道x2，知道了x2，就能知道x3,依次下去。我们把具备这种形式的数列通项称为递推式。递推式在进行动态规划是最基础的方法，利用计算机能够解决许多问题，这些以后有机会再说。我们回到数列收敛上。

• 例2

我们知道数列xn极限是0，说明它是一个无穷小量。我们知道，不一样的无穷小量趋近于0的速度是不一样的：

进一步的，我们想知道数列xn是以哪种速度趋近于0的，因此，我们探讨：

所谓的等价，在收敛角度来看，是指两个数列收敛的速度是一样的。这一点以后在函数极限会深入讲解。

• 例3

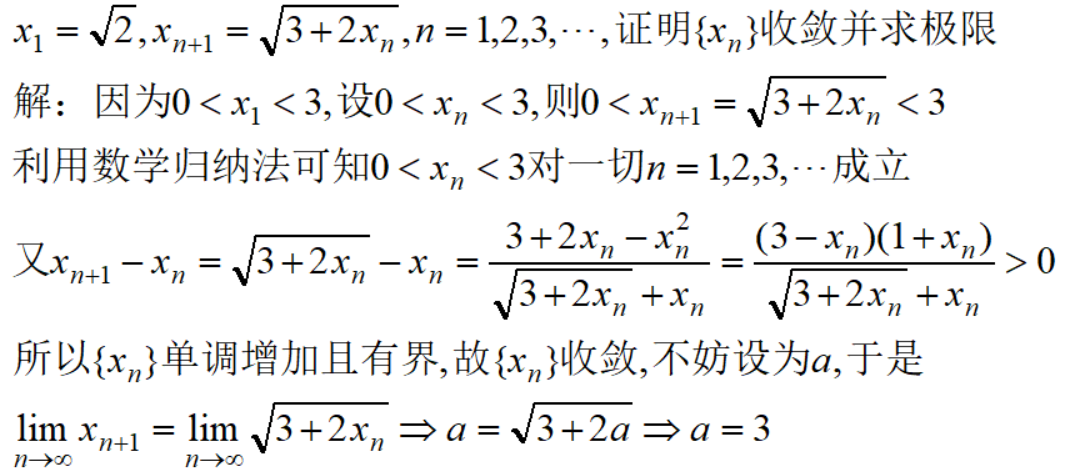
上面三个例子都是具备递推式的数列，首先证明数列单调有界，再利用其极限唯一性去求解。

Part2

但现实中，更多情况是递推式不明确，且数列不一定是单调的。下面我们通过一个例子来初步感受有界不单调数列但收敛的求解思想。

• 例4

斐波那契（Fibonacci），是意大利数学家，他提出了著名的斐波那契数列，也称兔子数列：

假设有一对兔子，经过一个季度可以到成长期，再经过一个季度可以到成熟期，成熟期的兔子可以生出1对兔子，生下来的兔子也都是经过成长期到成熟期，然后又可以生出1对兔子。假设兔子不会死，每次都是只生1对兔子

我们首先模拟一下前七个季度处于小兔、成长期和成熟期的数量，很容易得到下面一张表格：

季度	小兔对数	成长期对数	成熟期对数	总对数
1	1	0	0	1
2	0	1	0	1
3	1	0	1	2
4	1	1	1	3
5	2	1	2	5
6	3	2	3	8
7	5	3	5	13

接下来，我们来找递推式：

从递推式可以看出，兔子的总对数是无限增长的，也就是该数列是无穷大量。但我们更关心其增长率：

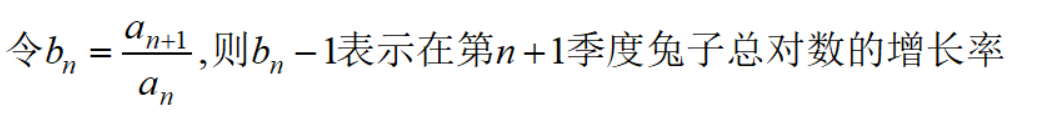
接下来讨论数列{bn}，看看是否收敛。

正好增长率为黄金分割点，因此斐波那契数列又称为黄金分割数列，它的增长率极限为0.618.

上面证明过程有两点需要注意，第一点是分界点的确定，其实是先假设bn收敛，那么可以得到：

这样就能确定临界点。

第二点是讨论偶数项的时候，讨论到偶数项单调减少，但只确定了有下界：

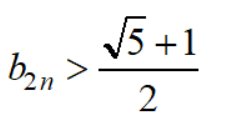
但我们直接说有界，严格意义上，还要证明其有上界，但事实上很简单，因为b2n单调减少，所以只要知道b2，我们就证明了偶数项有界：