线性规划的对偶理论

1.理解LP问题的对偶变量含义

2.熟悉LP规划模型的定性和定量灵敏度分析

3.原问题与对偶问题是看同一个问题的不同视角

4.强对偶性是KKT条件成立是充分必要条件

5.掌握对偶单纯形法的详细流程，并体会与单纯形法的差异

线性规划（LP）是最基础的运筹优化模型，我们已经对它有了初步的认识，并学会了第一种求解方法——单纯形法。今天，我们进一步分析它，考虑模型结果对输入参数或常量变动的灵敏度。我们要用到一个新的案例（混料模型）：

钢铁行业里，为了生产出满足各种化学成分要求的合金产品，金属废料需要加入一些纯添加剂来最大程度利用原材料。这是一个典型的混料问题。但由于添加剂极为昂贵，因此需要详细规划。而瑞典一家钢铁厂计划生产1000千克的熔炉进料，所有钢材的主要原材料是铁，下表列举了4种废料中碳、镍、铬、钼微量元素的含量比、可用数量以及单位成本(以瑞典货币克朗计量)。同时，表中也列出了3种可用的高成本纯添加剂以及最终混料中各种元素允许的含量范围。

显然，该问题的具体模型为：

1

定性灵敏度分析

LP问题的灵敏度分析包括约束条件的系数和目标函数系数，前者又分为右端系数（RHS）和左端系数（LHS）。首先我们来考虑约束条件。

我们知道，约束条件可以分为松约束和紧约束。当放宽一个约束后，可行域增加了，对应的最优值只能不变或者更优，收紧一个约束后，最优值只能不变或更差。具体怎么评判系数变化对约束松紧的影响，我们要具体分析。我们利用上面的“瑞典钢铁厂”案例来加以说明。

比如，假设其他参数不变，下图展示了改变废料1供给量限制的右端系数对目标最优值的影响：

可以看到，随着右端系数的增加，碎片1的可行域范围变大，对应最小化目标函数，最优值先逐渐减少，但不是线性递减，在经过第二个红色的点（60.4，10003.023）后减少速率变慢，最后在第四个红点（83.3，9925.5185）后速率变为0.期间经过第三个红点（75，9953.6717），也即原来约束条件的右端系数。

我们在来看其他参数不变，改变铬最低限制对最优值的影响：

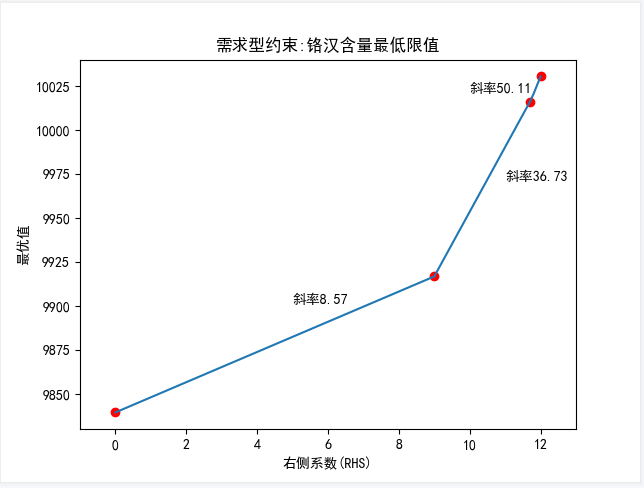
随着右端系数的增加，铬最低限制的可行域范围变小，对应最小化目标函数，最优值逐渐变大，但不是线性递增，在经过第二个红色的点（9，9916.944）后上升速率变快，最后在第三个红点（11.7，10016.108）后速率变得更大.最后在第四个红点（12，10030.472）速率变为无穷大（不可行）。

我们把类似这种“≤ ”的约束称为供给型约束，它的右端系数增加会放松约束，右端系数减少则收紧约束；把“≥” 的约束称为需求型约束，它的右端系数增加会收紧约束，右端系数减少则放松约束。

同理，左端系数变化也会对最优值有影响。假设其他参数不变࿰