R语言卡方(chisq)分布

最新推荐文章于 2025-02-09 00:04:42 发布

qq_27390023

最新推荐文章于 2025-02-09 00:04:42 发布

阅读量1.7w

点赞数 11

文章标签： r语言概率论

本文链接：https://blog.csdn.net/qq_27390023/article/details/125227780

版权

本文介绍了标准正态分布的基本概念，重点阐述了当多个独立随机变量服从标准正态分布时，其平方和形成卡方分布的特性。通过实例演示了如何使用R语言的rchisq、dchisq和pchisq函数进行抽样、概率密度计算及累积概率查询。涵盖了卡方分布的函数使用和非中心卡方分布的介绍。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。

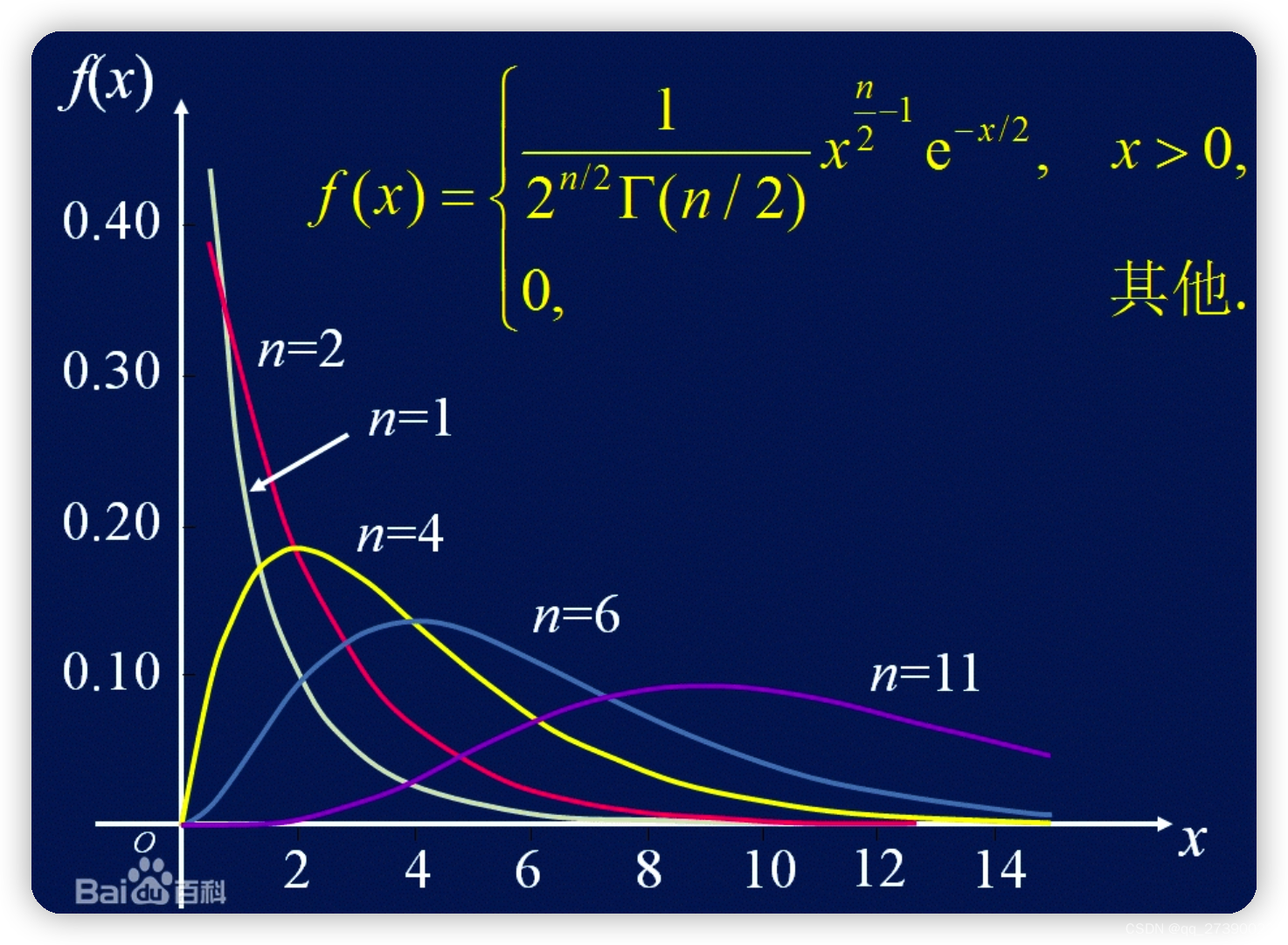
The (non-central) Chi-Squared Distribution

Description

Density, distribution function, quantile function and random generation for the chi-squared (chi^2) distribution with df degrees of freedom and optional non-centrality parameter ncp.

Usage

dchisq(x, df, ncp = 0, log = FALSE)
pchisq(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qchisq(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
rchisq(n, df, ncp = 0)

Arguments

`x, q`	vector of quantiles.
`p`	vector of probabilities.
`n`	number of observations. If `length(n) > 1`, the length is taken to be the number required.
`df`	degrees of freedom (non-negative, but can be non-integer).
`ncp`	non-centrality parameter (non-negative).
`log, log.p`	logical; if TRUE, probabilities p are given as log(p).
`lower.tail`	logical; if TRUE (default), probabilities are P[X ≤ x], otherwise, P[X > x].

####卡方(chisq)分布
# 1.卡方分布中抽样函数rchisq
n = 100
df <- 10
rchisq(n, df, ncp = 0)

# 2.卡方分布概率密度函数
x <- seq(0,30,0.1) # x为非负整数，表达次数。
y <- dchisq(x,df)
plot(x,y)

# 3.卡方分布累积概率
x <- seq(1,20,0.1)
plot(x,dchisq(x,df=10))
# P[X ≤ x]
pchisq(5, df=10)
# P[X > x]
pchisq(5, df=10,lower.tail = FALSE)

# probabilities p are given as log(p).
pchisq(5, df=10,log.p = TRUE)

# 4.qchisq函数(pchisq的反函数)
# 累积概率为0.95时的x值
qchisq(0.95, df=1)
qchisq(0.95, df=10)
qchisq(0.95, df=100)