支持向量机(SVM)(二)

前言

上篇博客已经推导出了原始最优化问题，这篇博客将会将问题利用拉格朗日对偶化使问题的到简化以方便处理。

拉格朗日对偶

让我们先暂时把SVM和最大化间隔分类器搁置在一边，来讨论解决限制最优化问题。
考虑一个如下形式的问题：
$min_w f(w)$
$s.t. h_i(w)=0,i=1,...,l$
我们使用拉格朗日数乘法来解决这个问题。在这个方法中，我们定义拉格朗日方程为：
$\mathcal{L}(w,\beta)=f(w)+\underset{i=1}{\overset{l}{\sum}}\beta_ih_i(w)$
这里，$\beta_i$叫做拉格朗日乘数。我们可以通过令偏导数等于0来解决找到符合条件的$w$和$\beta$:
$\frac{\partial \mathcal{L}}{\partial w_i} =0$;$\frac{\partial \mathcal{L}}{\partial \beta_i} =0$;
在这节中，我们将会泛化等式约束最优化问题到不等式约束。
考虑下面的问题我们称之为原始最优化问题：
$min_wf(w)$
$s.t. g_i(w)\le0,i=1,....,k$
$h_i(w)=0,i=1,.....,l$
为了解决这个问题，我们首先定义泛化拉格朗日方程：
$\mathcal{L}(w,\alpha,\beta)=f(w)+\underset{i=1}{\overset{k}{\sum}}\alpha_ig_i(w)+\underset{i=1}{\overset{l}{\sum}}\beta_ih_i(w)$
这里，$\alpha_i$和$\beta_i$叫做拉个朗日乘数，考虑这个等式：
$\Theta_{\mathcal{P}}(w)=\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}{\mathcal{L}(w,\alpha,\beta)}$
这里“$\mathcal{P}$”代表“原始”。如果$w$违反了任何原始约束条件（如果$g_i(w)\gt0$或者$h_i(w)\neq0$对于一些i）
你可以证实：
$\Theta_{\mathcal{P}}(w)=\infty$
因此，$\Theta_{\mathcal{P}}$在所有的$w$满足初始条件的情况下与目标问题获得相同的值。因此，如果我们考虑最小化问题
$\underset{w}{\mathrm{min}}\Theta_{\mathcal{P}}(w)=\underset{w}{\mathrm{min}}\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\mathcal{L}(w,\alpha,\beta)$
我们看到这和我们描述的原始问题相同。在接下来，我们同样定义最优化值的目标为：$p^*=\underset{w}{\mathrm{min}}\Theta_{\mathcal{P}}(w)$
现在来让我看一个有点不同的问题。我们定义：
$\Theta_\mathcal{D}(\alpha,\beta)=\underset{w}{\mathrm{max}}\Theta_{\mathcal{P}}(w)$
这里的$\mathcal{D}$代表的是”对偶”。介于定义$\Theta_\mathcal{P}$是使问题最优化对应的$\alpha,\beta$,这里代表的是使问题最小化对应的$w$。
现在我们能提出对偶最优化问题：
$\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\Theta_{\mathcal{D}}(\alpha,\beta)=\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\underset{w}{\mathrm{min}}\mathcal{L}(w,\alpha,\beta)$
这里和我们之前提到的问题完全相同，除了”max”和”min”的顺序改变了。我们同样定义对偶问题的最优化值为$\mathcal{d}^*=\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\Theta_{\mathcal{D}}(\alpha,\beta)$对偶问题和原始问题是如何联系在一起的？可以通过下式：
$\mathcal{d}^*=\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\Theta_{\mathcal{D}}(\alpha,\beta)\le\underset{w}{\mathrm{min}}\underset{\alpha,\beta:\alpha_i\ge0}{\mathrm{max}}\mathcal{L}(w,\alpha,\beta)=p^*$因此，在某些特定的条件下我们可以得到：$d^*=p^*$
因此我们就可以通过对偶问题代替原始问题。让我们来看看条件是什么。
假设$f$和$g_i$和$h_i$是凸优化问题。假设存在一些$w$使对于所有$i$满足条件$g_i(w)\lt0$.
基于上面的假设，一定存在这样的$w^*,\alpha^*,\beta^*$，其中$w^*$是原始问题的解，$\alpha^*,\beta^*$是对偶问题的最优解，同时$p^*=d^*=\mathcal{L}(w^*,\alpha^*,\beta^*)$。同时$w^*,\alpha^*和\beta^*$满足KKT条件如下：

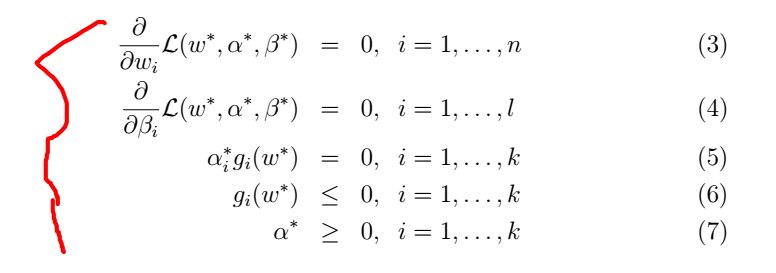
如果，一些$w^*,\alpha^*,\beta^*$满足KKT条件，那么他们同时也是原始问题和对偶问题的解。
我们把注意力放在等式(5),叫做KKT对偶互补条件。特别的，它暗示了如果$\alpha_i^*\gt0$,那么$g_i(w^*)=0$(比如”$g_i(w)\le0$”约束条件满足，意味着此时满足等式而不是不等式)之后我们将会证明SVM只有很少的支持向量；当我们使用SMO算法时，KKT对偶互补条件同时也会提供我们收敛测试。

2 最优化间隔分类器

之前我们为了找到最优化间隔分类器我们提出的原始最优化问题如下：
$\mathrm{min}_{\gamma,w,b}\frac{1}{2}||w||^2 s.t. y^{(i)}(w^Tx^{(i)}+b)\ge1,i=1,…,m$
我们可以把约束条件表示为：
$g_i(w)=-y^{(i)}(w^Tx^{(i)}+b)+1\le0$
我们对于每个训练样例都有这样的约束条件。由于KKT对偶互补条件，我们可以得到只有训练样例的$\alpha_i\gt0$才能得到函数间隔等于1（等价于对应的约束条件满足$g_i(w)=0$。考虑下图，其中最大间隔分隔超平面用实线表示。

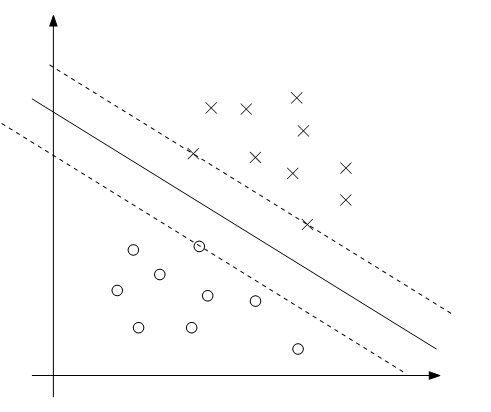
离决策边界最近的点就是有最小间隔的点；这里，有三个点（两正一负）位于平行于决策边界的虚线上，他们对应的$\alpha$是非零的对于最优解问题。这三个点在这个问题里被叫做支持向量。事实是支持向量要比训练集少的很多将会在以后有用。
我们构造我们最初的最优化问题的拉格朗日方程：
$\mathcal{L}(w,b,\alpha)=\frac{1}{2}||w||^2-\underset{i=1}{\overset{m}{\large \sum}}\alpha_i[y^{(i)}(w^Tx^{(i)}+b-1]$ (8)
让我们找出这个问题的对偶问题。首先，我们要找出使$\mathcal{L}(w,b,\alpha)$最小化对应的$w,b$(固定$\alpha$),得到了$\Theta_\mathcal{D}$，因此我们需要对$\mathcal{L}$做关于w和b的偏导数并使之等于0。我们有:
$\nabla\mathcal{L}(w,b,\alpha)=w-\underset{i=1}{\overset{m}\sum}\alpha_iy^{(i)}x^{(i)}=0$
因此可以得到：
$w=\underset{i=1}{\overset{m}\sum}\alpha_iy^{(i)}x^{(i)}$ (9)
对b求导可以得：
$\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha)=\underset{i=1}{\overset{m}\sum}\alpha_iy^{(i)}=0$ (10)
如果我们把等式(9)带回到拉格朗日方程组，化解可以得到：

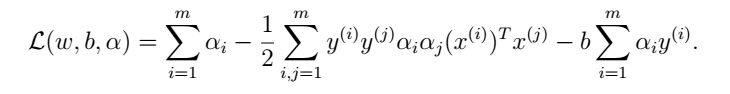
由于等式（10）最后一项等于0:，可以得到：

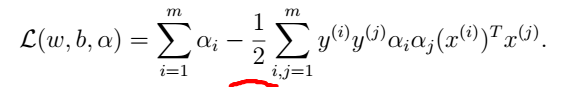
回想我们得到上述等式通过使最小化$\mathcal{L}$对应的$w,b$，把这些和约束条件$\alpha_i\ge0$和约束条件(10),我们获得如下的对偶问题：

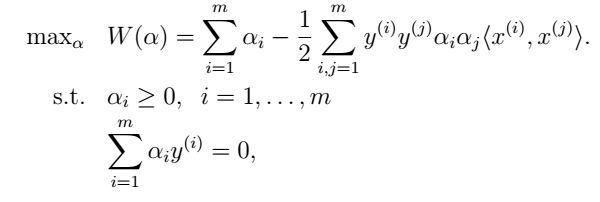
可以证实其确实满足KKT条件。因此我们可以用对偶问题代替原始问题。特别的，对偶问题中，我们要得到最大化问题对应的参数$\alpha_i$,在找到$\alpha$之后可以通过等式(9)来求得$w$。在已经找到$w^*$之后，考虑原始问题，我们可以通过下式求出$b^*$：

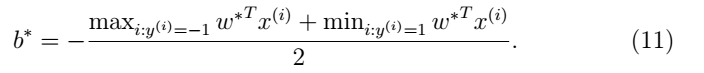
在等式（9）中，假设我们已经找到了一个训练样集的参数模型，我们想要预测一个新输入点x的值。我们可以计算$w^Tx+b$并且预测y=1当且仅当值大于0，但是使用（9）可以得到如下等式：

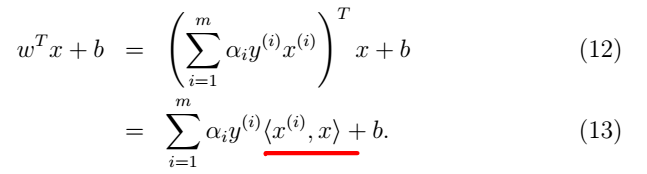
因此，如果我们已经找到了$\alpha_i$为了做预测我们要让$x$和所有的训练样例做内积。然而我们之前讨论过大多数的$\alpha_i$将会等于0。因此，这个和里大部分的数将会是0，但是我们确实需要做 x <script type="math/tex" id="MathJax-Element-46089">x</script>和支持向量的内积做预测。
下一篇博客将会介绍核，从而进一步提高SVM算法在高维空间的有效性。