说明:以后前一部分主要讲各种定义以及定理,用题目对定理来进行说明则放到后一板块
定义: 中的一个子空间是
中的集合H,具有以下三个性质:
a. 零向量属于H
b. 对H 中的任何向量u和v,u+v属于H
c. 对H中任意向量u和数c,c u属于H
即子空间对加法和标量乘法是封闭的
仅含零向量的子空间称为零子空间
中子空间H 的一组基是H 中一个线性无关组,它生成H
矩阵A的列空间的A的各列的线性组合的集合,记作 Col A
矩阵A的零空间是齐次方程的所有解的集合,记作 Nul A
当线性方程组写成的形式,Col A就是所有事方程有解的向量b的集合
矩阵A的主元列构成Col A的基
方程的解的参数形式实际上就是确定Nul A的基
非零子空间H 的维数,用dim H 表示,是H 的任意一个基的向量个数,零子空间的维数定义为零
矩阵A的秩(rank A)是A的列空间的维数,因为A的主元列形成Col A的一个基,A的秩正好是A的主元列的个数
秩定理:如果一个矩阵A有n列,则 rank A+ dim Nul A = n
最后接着上次最后给出的定理继续给出一些等价命题
设A为矩阵,则下列命题是等价的:
m. A的列向量构成的一个基
n. Col A=
o. dim Col A=n
p. rank A=n
q. Nul A={0}
r. dim Nul A=0
求的零空间的基
首先把方程的解写成参数向量的形式
通解为为自由变量
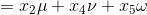
生成Nul A
注:设,虽然H 中的点也在
中,但它构成的是一个平面,映射
是H 和
之间保持线性组合关系的一一对应映射,我们称这种映射是同构的且H 与
同构,即若矩阵A是3x5的,有三个主元列,则Nul A
这一讲就到这里,我们下次继续~








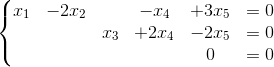

















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








