Generate & Rank: A Multi-task Framework for Math Word Problems

摘要

数学单词问题（MWP）是自然语言处理中的具有挑战性且重要的任务。许多最近的研究将MWP定义为生成任务，并采用了序列到序列模型来将问题描述转换为数学表达式。然而，数学表达式易于生成较小的错误，而生成目标无法明确处理这种错误。为解决此限制，我们为MWP设计了一个新的排名任务，并提出了一种基于生成预训练语言模型的多任务框架，Generate & Rank。通过生成和排名的联合训练，模型能从自己的错误中学习，且能够区分正确和不正确的表达式。同时，我们专为MWP和在线更新而设计基于树的加噪，以提高排名器。我们展示了我们提出的方法对基准测试的有效性，结果表明，我们的方法始终优于所有数据集中的基线。特别是，在经典的Math23K中，我们的方法比SOTA高了7％（78.4％→85.4％）。

1.介绍

　　解决数学单词问题（MWP）是自然语言处理（NLP）中的一个重要且基本的任务，其需要基于给定的数学问题描述来提供一个解决表达式，如表1所示。最近的研究将MWP定义为生成任务，并且通常采用基于LSTM的序列到序列（Seq2Seq）模型，其中问题文本是源序列，数学表达式是目标序列，模型需要建模从源文本到目标表达式的映射。这些研究提出了许多先进的技术来改善MWP求解器，但它们的性能仍然不能令人满意。
　　我们认为将MWP作为生成任务来建模时不够的，因为数学表达式和自然语言序列之间存在显着差异：数学表达中的一个小错误将改变整个语义，从而导致错误的答案，而自然语言对这种小错误具有很好的鲁棒性。生成任务的目标函数是在真实表达式上最大化生成概率，这没有明确的策略，使得模型学会区分正确的表达式和具有错误的表达。此外，先前的工作发现，随着表达式变长，生成模型的性能会迅速降低。
　　为了处理上述问题，我们提出了Generate & Rank，这是一个用于MWP的多任务框架，该框架引入了一个新的排名器，以显式区分正确和不正确的表达式。具体来说，我们的框架包括两个模块：生成器和排名器。前者旨在给定候选表达式，后者旨在对候选表达进行排名。它们是基于Encoder-Decoder模型构建的，并且使用生成损失和排名损失来共同训练。在这项工作中，我们基于BART构建我们的模型，这是一个广泛使用的预训练的语言模型，可以在各种序列序列任务上实现SOTA性能。在多任务训练期间，生成器生成的表达式用于构建表达式库并训练排名器，以便模型可以从自己的错误中学习。为了对排名器构建更多的有信息候选表达式，我们专门为MWP设计基于树的加噪。我们还介绍了在线更新机制，以在每个训练时期生成一组新的候选表达式。整体训练过程以迭代的方式进行，其中排名器和生成器互相增强。
　　为了评估所提出的模型的有效性，我们在Math23k和Mawps的数据集上进行了广泛的实验。结果表明，我们的模型优于传统的基线。特别是，我们在广泛研究的Math23k数据集中获得了7％的提升。此外，我们进行了消融研究和模型分析，表明（1）联合训练改善了生成器和排名器的性能；（2）建设候选表达和在线更新的两项策略对于排名器的性能非常重要。我们还发现，使用ranker，我们的模型在长表达式上实现了巨大改善。
　　我们的工作的贡献如下：（1）我们提出 Generate & Rank，这是一个新的多任务框架，用于训练一个预训练的用于数学单词问题的语言模型。为了构建对Ranker的信息丰富的候选表达式，我们提出了两种有效的生成方法，并引入了在线更新策略。（2）实验表明，我们提出的模型始终优于SOTA的模型，并在Math23K数据集上实现了显着改进。

2.预备知识

2.1 Math Word Problem

数学单词问题$P$是一系列单词和数值字符，其通常描述世界的部分数量状态以及数量之间的一些关系，然后询问关于未知数量的问题。问题的解决方案$S$是一个由数学运算符和数字组成的数学表达式。在解决数学单词问题时，我们通常不关心特定数值，因此问题和表达式中的数字会按他们在问题中的出现顺序被映射到特殊字符$NUM\#i$。表1给出了原始数学单词问题和相应数字映射问题的示例。

2.2 BART

BART是一种广泛使用的预训练语言模型。它遵循使用Transformer层的标准编码器 - 解码器结构，并用文本去噪任务进行预训练。预训练BART可以用于微调序列分类和生成的任务。
　　Transformer-based Encoder-Decoder。BART使用编码器 - 解码器结构，该结构是用于序列到序列任务的主流架构。编码器采用双向自注意力将输入的字符序列$P=(x_1,x_2,...,x_n)$映射到具有连续表示的输出序列$\text{R}=({\text{r}}_1,{\text{r}}_2,....,{\text{r}}_n)$。BART编码器由多个Transformer层组成，每个Transformer层由多头自注意力（MHA）模块和全连接的前馈（FFN）模块组成。我们将BART编码器的映射函数表示如下：
$$({\text{r}}_1,{\text{r}}_2,...,{\text{r}}_n)=BAR{T}_{Enc}(x_1,x_2,...,x_n)\text{\hspace{1em}(1)}$$
　　BART解码器还包括多个Transformer层。除了MHA和FFN模块外，解码器层会基于编码器的输出增加了另一个多头注意力。解码器一次接收一个字符$s_i$，并基于编码器的输出和解码器输入中先前的字符给出当前输出状态。然后将该输出状态带入线性变换，然后是$softmax$函数来获取预测的下一字符的概率。此一步解码过程表示如下：
$$P(\ast )=softmax({\text{d}}_i\text{W}+\text{b})\text{\hspace{1em}(2)}$$
$${\text{d}}_i=BAR{T}_{Dec}(\text{R};s_0,s_1,...,s_{i-1}),\text{\hspace{1em}(3)}$$
其中$s_0$是表示解码开始的特殊字符$[BOS]$，$\text{R}$是编码器的输出。
　　BART Pre-training。BART通过使用将损坏文档恢复到原始文档这一任务来进行预训练。BART的输入以两种方式来加噪：（1）用单个$[MASK]$字符替换多个文本跨度；（2）文档中的句子以随机顺序进行打乱。BART预训练的目标是最大限度地减少解码器预测序列与真实序列之间的交叉熵损失。

3.方法

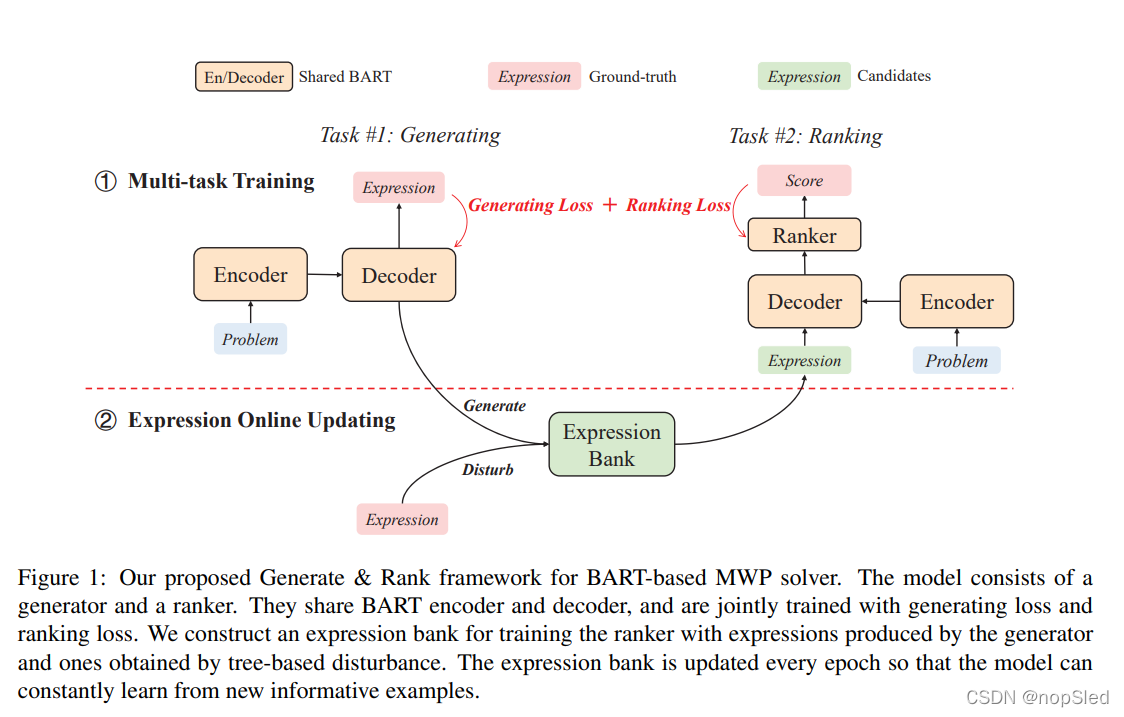
　　我们提出了Generate & Rank，这是基于BART的解决数学单词问题的多任务训练框架。我们的模型包括一个生成器和一个排名器，它们共享一个BART模型，并通过生成任务和排名任务进行联合训练。数学单词问题的生成目标是表达式，另外，我们还添加了排名任务，以便模型可以从一组候选者中选择正确的表达式。我们构建了一个表达式库，为排名器提供训练数据。图1显示了我们所提出的框架，我们在以下部分中介绍了每个任务和整个框架的详细信息。

3.1 Multi-task Training

Task #1: Generating。我们首先将数学单词问题作为序列到序列任务，其中BART被训练，以给定数学单词问题来生成对应表达式。与BART的微调策略类似，我们使用问题文本，即一个字符序列$P=(x_1,x_2,...,x_n)$，作为BART编码器的输入，并最小化预测表达式和目标表达式$S=(s_1,s_2,..,s_m)$的负对数似然：
$${\mathcal{J}}_{GEN}=\frac{1}{|\mathcal{D}|}\sum _{(P,S)\in \mathcal{D}}-logPr(S|P),\text{\hspace{1em}(4)}$$
其中，条件概率以自回归方式分解，如下所示：
$$Pr(S|P)=\prod _{i=1}^{m}Pr(s_i|P,S_{j<i})\text{\hspace{1em}(5)}$$
$$Pr(\ast |P,S_{j<i})=softmax({\text{d}}_i\text{W}+\text{b})\text{\hspace{1em}(6)}$$
$${\text{d}}_i=BAR{T}_{Dec}(\text{R};S_{j<i})\text{\hspace{1em}(7)}$$
$$\text{R}=BAR{T}_{Enc}(P).\text{\hspace{1em}(8)}$$
此外，我们添加了两个特殊的字符$s_1=[bos]$和$s_m=[eos]$，来表示解码序列的开始和结束。
　　Task #2: Ranking。通过生成，我们获得许多解决方案的候选表达式。要确定哪种表达式对问题来说是正确的解决方案，我们提出了一个排名任务，该任务基本上是序列对分类的任务。给定对问题和候选表达式，排名器选择具有最高排名分数的表达式作为问题的最终解决方案。具体来说，我们在最后一个解码器字符的最后层隐藏状态的顶部添加MLP分类器。最后一个解码器字符始终是一个特殊的[EOS]令牌，其相应的隐藏状态能够使用到问题文本和表达式中所有字符表示。与生成任务相同，我们将问题文本送入编码器，表达式送入解码器中，获取序列表示。然后将最后一个解码器字符的表示作为分数预测分类器的输入：
$$Pr(\cdot |P,S)=softmax({\text{d}}_{m+1}^{\prime })\text{\hspace{1em}(9)}$$
$${\text{d}}_{m+1}^{\prime }=tanh({\text{d}}_{m+1}{\text{W}}_1+{\text{b}}_1){\text{W}}_2+{\text{b}}_2$$
$$d_{m+1}=BAR{T}_{Dec}(\text{R};S)\text{\hspace{1em}(11)}$$
其中$\text{R}$是编码器的输出，$S$是表达式字符序列，${\text{d}}_{m+1}$是最后一个的解码器表示，并且${\text{W}}_{1|2}$和${\text{b}}_{1|2}$是可训练参数。排名器的训练目标是分类器输出和正确标签之间的交叉熵，
$${\mathcal{J}}_{RANK}=-\frac{1}{|{\mathcal{D}}^{+}\cup {\mathcal{D}}^{-}|}[\sum _{(P,S)\in {\mathcal{D}}^{+}}logPr(1|P,S)+\sum _{(P,S)\in {\mathcal{D}}^{-}}logPr(0|P,S)]\text{\hspace{1em}(12)}$$
其中${\mathcal{D}}^{+}$和${\mathcal{D}}^{-}$分别是正例和负例。我们在下一节介绍如何生成负例子。
　　Optimization Objective。我们一起联合两个损失来训练模型：
$$\mathcal{J}={\mathcal{J}}_{GEN}+{\mathcal{J}}_{RANK}.\text{\hspace{1em}(13)}$$
并且这两个任务都共享BART参数。

3.2 Expression Bank

　　根据定义，任何不等于真实表达式的候选表达式都可以作为负例，但由于计算资源有限，我们不能使用所有这些负例。为了有效地训练排名器，我们使用两种不同的策略，即基于模型的生成和基于树的加噪，来为排名器的训练构建一个表达式库。
　　Model-based Generation。第一个策略是用生成器生成新的表达式。具体地，给定一个问题，我们在生成器的结果上使用集束搜索来产生top-K个表达式。根据其计算结果是否等于真实表达式的结果，来为每个表达式标记为正例或负例。
　　Tree-based Disturbance。我们构建新表达式的第二种方式是基于真实表达式进行加噪。我们设计了四种加噪方法，如图2所示。真实表达式首先转换为抽象语法树（AST）。然后我们以四种方式来加噪树节点或子结构，以产生新表达式：a）Expand。将新操作和数字作为叶节点扩展到子树中。 b）Edit。将节点随机改变为另一个，同时保持表达有效（即，数字节点将被改变为另一个数字，以及操作节点被改变为另外一个操作）。 c）Delete。删除叶节点并用其兄弟节点替换其父节点。d）Swap。交换操作节点的左侧和右侧子项。
　　我们使用上述方法来构建了表达式库。由于新表达式也可以是正确的（例如，交换两个相加或相乘的操作数），我们将新获得的表达式的数值结果与真实表达式进行比较，并根据比较结果将它们添加到正例或负例中。然后，从这个表达式库中采样正负例对用于多任务训练。为了使模型学习信息丰富的例子，我们对表达式库进行了在线更新，这意味着我们在每个训练epoch都使用基于模型的生成和基于树的加噪来获得新的表达式。

3.3 Training Procedure

　　训练过程包括多任务训练和表达式的在线更新。我们首先为生成任务微调预训练BART（等式4中的${\mathcal{J}}_{GEN}$）。然后，我们使用微调后的BART和基于树的加噪来生成候选表达式作为排名器的训练样本。然后我们进行了生成和排名的联合训练。该过程以迭代方式进行，使得两个模块（即，generator和ranker）持续彼此增强。同时，每个epoch后更新排名器的训练样例。我们在算法1中总结了整体训练过程。

3.4 Model Inference

我们执行两阶段模型推理，即生成和排名。具体而言，给定新的问题文本序列$P$，我们首先将其传递给编码器以获取问题表示$\text{R}$。然后我们执行集束搜索以生成top-K个表达式。这些生成的表达式用作排名器的候选解决方案。所有表达式都传递给排名器，并选择最高分来作为最终结果。