Normalizing Flows for Probabilistic Modeling and Inference翻译

摘要

normalizing flows提供了一种定义复杂概率分布的通用机制，仅需要指定一个基本分布（非常简单）和一系列双映射变换。最近有很多关于使用normalizing flows的工作，范围从提高建模复杂分布的能力到扩展应用。 我们认为该领域现在已经成熟，并且需要将观点进行统一。在这篇综述中，我们试图通过从概率建模和推理两个方面来描述这些观点。我们特别强调flow设计的基本原理，并讨论了诸如分布建模能力和计算效率之间平衡等基本主题。我们还通过将flow与更通用的概率变换联系起来，以扩展flow的概念框架。最后，我们总结了如何将flow用于生成式建模，近似推理和有监督学习等任务。

1.介绍

搜索一个明确指定的概率模型（即能正确描述生成数据过程的模型）是统计科学的持久理想之一。但是，只有最简单的设置才能实现这一目标。因此，所有统计学和机器学习的核心需求是提出一个允许定义任意概率分布的工具和理论，因此，这使得开发更加明确的模型成为可能。
　　本文回顾了我们用来解决此需求的一种工具：将概率分布作为normalizing flows构建。normalizing flows通过一系列变换将简单的概率密度映射到更丰富，更多模式的分布，这就像流过一组管子的液体。正如我们将看到的那样，重复将简单变换应用到一个单峰初始密度分布，会导致生成精细复杂的分布。这种灵活性意味着flow可以应用到建模，推理和仿真等关键统计任务中。
　　normalizing flows是机器学习研究中越来越活跃的领域。然而，目前缺乏统一的观点来理解最新工作与先前工作的关系。Papamakarios (2019) 的论文和Kobyzev et al. (2020) 的调查已经在建立这种更广泛理解上做出了努力。我们的综述对这些现有论文进行了补充。 特别是，我们对flows的观点比Papamakarios (2019)更全面，但共享一些基本原则。Kobyzev et al. (2020) 的文章在文献的覆盖范围和综合程度上值得称赞，同时讨论了有限流和无限流（就像我们一样），并在密度估计中组织了最新结果。我们的综述本质上是一种教程，并对Kobyzev et al. (2020) 中的几个被标记为开放问题的领域提供了深入的讨论（例如离散变量的扩展和黎曼流形）。
　　我们对标准化流的探索试图阐明一种原则，这些原则将指导其在可预见的未来的建设和应用。具体而言，我们的综述首先在第2节中建立normalizing flows的形式和概念结构。Flow的构建细节分别在第三节（有限流）和第四节（无限流）中进行了描述，然后在第5节中提出了更通用的观点，这又允许扩展到结构化领域和几何形状。 最后，我们在第6节中讨论了常见的应用。
　　Notation。我们使用粗体符号来表示向量（小写）和矩阵（大写），其余变量为标量。我们使用$Pr(\cdot )$表示概率，使用$p(\cdot )$表示概率密度。我们还将使用$p(\cdot )$表示具有该密度函数的分布。我们经常向概率密度添加下标（例如$p_x(\text{x})$）强调它们所指的随机变量。符号$p(\text{x};\text{θ})$代表具有分布参数$\text{θ}$的随机变量$\text{x}$的分布。符号${\nabla }_{\text{θ}}$代表梯度运算符，该梯度运算符收集所有与$\text{θ}$相关的偏导数，即对于$K$维参数有${\nabla }_{\text{θ}}f=[\frac{\partial f}{{\partial }_{{\theta }_1}},...,\frac{\partial f}{{\partial }_{{\theta }_K}}]$。函数$f:{\mathbb{R}}^D\to {\mathbb{R}}^D$的雅可比矩阵比被表示为$J_f(\cdot )$。最后，我们使用符号$\text{x}〜p(\text{x})$表示从分布$p(\text{x})$中采样或模拟的变量$\text{x}$。

2.Normalizing Flows

我们首先概述normalizing flows的基本定义和属性。我们建立了基于flow的模型的表现力，这解释了如何在实践中使用flows，并提供一些历史背景。本节不要求事先对normalizing flows熟悉，并且可以作为该领域的介绍。

2.1 Definition and Basics

　　normalizing flows提供了一种在连续随机变量上构建灵活概率分布的通用方法。令$\text{x}$为$D$维真实矢量，假设我们想定义$\text{x}$上的联合分布。基于flow建模的主要思想是将$\text{x}$表示为从$p_u(\text{u})$中采样的真实向量$\text{u}$的变换$T$：
$$\text{x}=T(\text{u})where\text{u}\sim p_u(\text{u}).\text{\hspace{1em}(1)}$$
　　我们将$p_u(\text{u})$称为flow模型的基本分布。变换$T$和基本分布$p_u(\text{u})$可以具有自己的参数（分别为$\varphi$和$\psi$）；这产生了由 { ϕ , ψ } \{\phi,ψ\} {ϕ,ψ}参数化的$\text{x}$上的一系列分布。
　　flow模型的一个属性是变换$T$必须是可逆的，且$T$和$T^{-1}$必须是可微分的。这种变换被称为diffeomorphisms(可微分变换)，同样也要求$\text{u}$是D维的。在这些条件下，$\text{x}$的密度分布定义明确，且可以通过变量变换来获得：
$$p_x(\text{x})=p_u(\text{u})|det{J}_T(\text{u}){|}^{-1}where\text{u}=T^{-1}(\text{x}).\text{\hspace{1em}(2)}$$
　　同样地，我们还可以根据$T^{-1}$的雅可比矩阵来编写$p_x(\text{x})$：
$$p_x(\text{x})=p_u(T^{-1}(\text{x}))|det{J}_{T^{-1}}(\text{x})|.\text{\hspace{1em}(3)}$$
　　雅可比矩阵 $J_T(\text{u})$是$T$的所有偏导数组成的$D\times D$矩阵：
$$J_T(\text{u})=\left[\begin{array}{ccc}\frac{\partial T_1}{\partial u_1}& \cdots & \frac{\partial T_1}{\partial u_D}\\ ⋮& \ddots & ⋮\\ \frac{\partial T_D}{\partial u_1}& \cdots & \frac{\partial T_D}{\partial u_D}\end{array}\right].\text{\hspace{1em}(3)}$$
　　实际上，我们通常通过使用神经网络来实现$T$（或$T^{-1}$），以构建基于流的模型，并将$p_u(\text{u})$作为一个简单密度分布，例如多元正态分布。在第3和4节中，我们将详细讨论如何实现$T$（或$T^{-1}$）。
　　直观上，我们可以将变换$T$视为对空间${\mathbb{R}}^D$的扭曲，以将分布$p_u(\text{u})$变换到$p_x(\text{x})$中。雅可比行列式的绝对值$|det{J}_T(\text{u})|$量化了由$T$导致的$\text{u}$的一个极小空间的相对变化。即，令$\text{du}$为$\text{u}$附近的一个较小空间，$\text{dx}$为$\text{x}$附近的一个较小空间，且由$\text{du}$变换得到。然后，我们有$|det{J}_T(\text{u})|\approx Vol(\text{dx})/Vol(\text{du})$，即$\text{dx}$的大小除以$\text{du}$的大小。同时，$\text{dx}$中的概率质量必须等于$\text{du}$中的概率质量。 因此，如果$\text{d}u$被扩展，则$\text{x}$处的密度小于$\text{u}$处的密度。 如果$\text{d}u$收缩，则$\text{x}$处的密度更大。
　　可逆和可微分变换的一个重要属性是可组合的。给定两个这样的变换$T_1$和$T_2$，它们的组合$T_2◦T_1$也是可逆的和可微分的。它的逆和雅各比行列式如下所示：
$$(T_2◦T_1{)}^{-1}=T_1^{-1}◦T_2^{-1}\text{\hspace{1em}(5)}$$
$$det{J}_{T_2◦T_1}(\text{u})=det{J}_{T_2}(T_1(\text{u}))\cdot det{J}_{T_1}(\text{u}).\text{\hspace{1em}(6)}$$
　　因此，我们可以通过组合多个简单变换来构建复杂变换，而不会损害可逆性和可微分的要求，因此也不会失去计算密度$p_x(\text{x})$的能力。
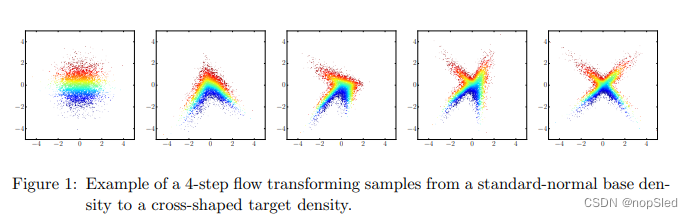
　　在实践中，通常将多个变换$T_1,...,T_K$结合在一起来获得$T=T_K◦\cdots ◦T_1$是很常见的，其中每个$T_k$将${\text{z}}_{k-1}$转换为${\text{z}}_k$，假设${\text{z}}_0=\text{u}$且${\text{z}}_K=\text{x}$。因此，术语“‘flow’”是指从$p_u(\text{u})$中获得的样本集通过变换序列$T_1,...,T_K$逐渐发生变换的轨迹。“normalizing”是指从$p_x(\text{x})$中获得的样本集通过逆flow序列$T_K^{-1},...,T_1^{-1}$，将其转换为服从密度$p_u(\text{u})$的样品集（通常被认为是多元正态分布 ）。图1说明了将标准正态基本分布转换为十字形状的目标密度的flow（$K=4$）。
　　在功能方面，基于flow的模型提供了两个操作：通过公式(1)从模型中进行采样，或者通过公式(3)来评估模型的密度。这些操作具有不同的计算要求。从模型采样要求具有从$p_u(\text{u})$采样并计算正向变换$T$的能力。评估模型密度要求具有计算逆向变换$T^{-1}$和其雅可比行列式，并评估密度$p_u(\text{u})$的能力。这种应用将决定需要采用哪些操作以及它们需要的效率。我们在第3和4节中使用各种实现方式讨论了相关的操作和计算的权衡。

2.2 Expressive Power of Flow-Based Models

在讨论flows的细节之前，最重要的问题是：基于flow模型的表现性如何？ 即使基本分布简单，它们也可以表示任何分布$p_x(\text{x})$吗？我们表明，在$p_x(\text{x})$具有合理条件的情况下，这种通用表示是可能的。具体而言，我们将证明，对于任何一对目标分布$p_x(\text{x})$和基本分布$p_u(\text{u})$，存在将$p_u(\text{u})$变成$p_x(\text{x})$的可微分变换。该论点是建设性的，是基于Hyv¨arinen and Pajunen (1999) 的非线性ICA存在的类似证明。
　　假设对于所有的$\text{x}\in {\mathbb{R}}^D$，有$p_x(\text{x})>0$，并假设所有条件概率$Pr(x_i^{\prime }\le x_i|{\text{x}}_{<i})$相对于$(x_i,{\text{x}}_{<i})$是可微分的。使用概率链式法则，我们可以将$p_x(\text{x})$分解为条件密度的乘积，如下所示：
$$p_x(\text{x})=\prod _{i=1}^D{p}_x(x_i|{\text{x}}_{<i}).\text{\hspace{1em}(7)}$$
由于$p_x(\text{x})$每一个地方都是非零的，即$p_x(x_i|{\text{x}}_{<i})>0$。接下来，定义变换$F:\text{x}\mapsto \text{z}\in (0,1{)}^D$，其第$i$个元素由第$i$个条件密度的累积分布函数(CDF)给出：
$$z_i=F_i(x_i,{\text{x}}_{<i})={\int }_{-\infty }^{x_i}{p}_x(x_i^{\prime }|{\text{x}}_{<i})d{x}_i^{\prime }=Pr(x_i^{\prime }\le x_i|{\text{x}}_{<i}).\text{\hspace{1em}(8)}$$
由于每个$F_i$相对于其输入都是可微分的，因此相对于$\text{x}$也是可微分的。并且，每个$F_i(\cdot ,{\text{x}}_{<i}):\mathbb{R}\mapsto (0,1)$是可逆的，因为它的导数$\frac{\partial F_i}{\partial x_i}=p_x(x_i|{\text{x}}_{<i})$都是正的。因为$z_i$不依赖于$i<j$的$x_j$，这意味着我们可以反转$F$，其对每个元素的逆$F_i^{-1}$如下：
$$x_i=(F_i(\cdot ,{\text{x}}_{<i}){)}^{-1}(z_i)fori=1,...,D.\text{\hspace{1em}(9)}$$
　　$F$的雅可比矩阵是下三角形矩阵，因为丢$i<j$，有$\frac{\partial F_i}{\partial x_j}=0$。因此，$F$的雅可比行列式等于其对角线元素的乘积：
$$det{J}_F(\text{x})=\prod _{i=1}^D\frac{\partial F_i}{\partial x_i}=\prod _{i=1}^D{p}_x(x_i|x_{<i})=p_x(\text{x}).\text{\hspace{1em}(10)}$$
　　由于$p_x(\text{x})>0$，因此雅可比行列式是非零的。因此，存在$J_F(\text{x})$的逆，等于$F^{-1}$的雅可比矩阵，因此$F$是可微分变换。使用变量变换定理，我们可以按以下方式计算$z$的密度：
$$p_z(\text{z})=p_x(\text{x})|det{J}_F(\text{x}){|}^{-1}=p_x(\text{x})|p_x(\text{x}){|}^{-1}=1,\text{\hspace{1em}(11)}$$
这意味着$\text{z}$在$(0,1{)}^D$中服从均匀分布。
　　上述观点表明，即使我们将基本分布限制为$(0,1{)}^D$中的均匀分布，基于流的模型也可以表达任何分布$p_x(\text{x})$（满足上述条件）。我们可以首先将$\text{u}$变换到均匀分布$\text{z}\in (0,1{)}^D$，以作为中间步骤，从而将此观点扩展到任何基本分布$p_u(\text{u})$（满足与$p_x(\text{x})$相同的条件）。特别地，对于任何满足上述条件的$p_u(\text{u})$，可以将$G$定义为以下变换：
$$z_i=G_i(u_i,{\text{u}}_{<i})={\int }_{-\infty }^{u_i}{p}_u(u_i^{\prime }|{\text{u}}_{<i})d{u}_i^{\prime }=Pr(u_i^{\prime }\le u_i|{\text{u}}_{<i}).\text{\hspace{1em}(12)}$$
通过与上述相同的观点，$G$是可微分变换，$\text{z}$在$(0,1{)}^D$中服从均匀分布。因此，带有变换$T=F^{-1}$的flow可以将$p_u(\text{u})$变成$p_x(\text{x})$。

2.3 Using Flows for Modeling and Inference

与拟合任何概率模型类似，将一个基于flow的模型$p_x(\text{x};\text{θ})$拟合到目标分布$p_x^{\ast }(\text{x})$是可以通过最小化它们之间的散度或差异来完成。最小化是通过优化模型参数 θ = { ϕ , ψ } \textbf θ=\{\textbf ϕ, \textbf ψ\} θ={ϕ,ψ}来完成的，其中$\text{ϕ}$是变换$T$的参数，$\text{ψ}$是基本分布$p_u(\text{u})$的参数。在以下各节中，我们讨论了一些用于拟合flow模型的散度，特别关注Kullback–Leibler (KL)散度，因为它是最受欢迎的选择之一。

2.3.1 Forward KL Divergence and Maximum Likelihood Estimation

目标分布$p_x^{\ast }(\text{x})$与基于flow的模型$p_x(\text{x};\text{θ})$之间的前向KL散度可以写为如下所示：
$$\begin{gathered} \mathcal{L}(\text{θ})=D_{KL}[p_x^{\ast }(\text{x})||p_x(\text{x};\text{θ})] \\ =-{\mathbb{E}}_{p_x^{\ast }(\text{x})}[log{p}_x(\text{x};\text{θ})]+const. \\ =-{\mathbb{E}}_{p_x^{\ast }(\text{x})}[log{p}_u(T^{-1}(\text{x};\text{ϕ});\text{ψ})+log|det{J}_{T^{-1}}(\text{x};\text{ϕ})|]+const.\text{\hspace{1em}(13)} \end{gathered}$$
　　前向KL散度非常适合我们从目标分布采样（或生成它们）的情况，但是我们不一定能够评估目标密度$p_x^{\ast }(\text{x})$。假设我们有有一组来自$p_x^{\ast }(\text{x})$中的样本集 { x n } n = 1 N \{\textbf x_n\}^N_{n=1} {xn​}n=1N​，我们可以通过蒙特卡洛（Monte Carlo）来估计$p_x^{\ast }(\text{x})$的期望，如下所示：
$$\mathcal{L}(\text{θ})\approx -\frac{1}{N}\sum _{n=1}^{N}log{p}_u(T^{-1}({\text{x}}_n;\text{ϕ});\text{ψ})+log|det{J}_{T^{-1}}({\text{x}}_n;\text{ϕ})|+const.\text{\hspace{1em}(14)}$$
最小化上述KL散度的蒙特卡洛近似相当于通过最大似然估计将基于flow的模型拟合到样本集上 { x n } n = 1 N \{\textbf x_n\}^N_{n=1} {xn​}n=1N​。
　　实际上，我们通常使用基于随机梯度的方法在迭代中优化参数$\text{θ}$。我们可以获得KL散度相对于参数的无偏梯度估计，如下所示：
$${\nabla }_{\text{ϕ}}\mathcal{L}(\text{θ})=\frac{1}{N}\sum _{n=1}^N{\nabla }_{\text{ϕ}}log{p}_u(T^{-1}({\text{x}}_n;\text{ϕ});\text{ψ})+{\nabla }_{\text{ϕ}}log|det{J}_{T^{-1}}({\text{x}}_n;\text{ϕ})|\text{\hspace{1em}(15)}$$
$${\nabla }_{\text{ψ}}\mathcal{L}(\text{θ})=\frac{1}{N}\sum _{n=1}^N{\nabla }_{\text{ψ}}log{p}_u(T^{-1}({\text{x}}_n;\text{ϕ});\text{ψ}).\text{\hspace{1em}(16)}$$
　　如果$p_u(\text{u};\text{ψ})$接受闭式的最大似然估计，那么关于$\text{ψ}$的更新也可以以闭式进行，例如高斯分布的情况。
　　为了通过最大似然拟合基于flow的模型，我们需要计算$T^{-1}$，其雅可比行列式以及密度分布$p_u(\text{u};\text{ψ})$，如果使用基于梯度的优化，则可以对这三项进行微分。这意味着即使我们无法计算$T$或从$p_u(\text{u};\text{ψ})$中采样，我们也可以训练具有最大似然的flow模型。但是，如果我们要在模型拟合后从模型中采样$\text{x}$，则仍然需要这些操作。

2.3.2 Reverse KL Divergence

另外，我们可以通过最小化反向KL散度来拟合基于flow的模型，这可以写为：
$$\begin{gathered} \mathcal{L}(\text{θ})=D_{KL}[p_x(\text{x};\text{θ})||p_x^{\ast }(\text{x})] \\ ={\mathbb{E}}_{p_x(\text{x};\text{θ})}[log{p}_x(\text{x};\text{θ})-log{p}_x^{\ast }(\text{x})] \\ ={\mathbb{E}}_{p_u(\text{u};\text{ψ})}[log{p}_x(\text{u};\text{ψ})-log|det{J}_T(\text{u};\text{ϕ})|-log{p}_x^{\ast }(T(\text{u};\text{ϕ}))].\text{\hspace{1em}(17)} \end{gathered}$$
　　我们利用变量变换，以表示对$\text{u}$的期望。当我们有能力评估目标密度$p_x^{\ast }(\text{x})$，且不用从中采样时，反向KL散度是适合的。实际上，即使我们将$p_x^{\ast }(\text{x})$评估为乘法归一化常数$C$，我们也可以最小化$\mathcal{L}(\text{θ})$，因为在这种情况下，$logC$将是上述表达式$\mathcal{L}(\text{θ})$中的加法常数。因此，我们可以假设$p_x^{\ast }(\text{x})={\tilde{p}}_x(\text{x})/C$，其中${\tilde{p}}_x(\text{x})$是可处理的，但是$C=\int {\tilde{p}}_x(\text{x})d\text{x}$不是，并将反向KL散度重写为：
$$\mathcal{L}(\text{θ})={\mathbb{E}}_{p_u(\text{u};\text{ψ})}[log{p}_x(\text{u};\text{ψ})-log|det{J}_T(\text{u};\text{ϕ})|-log{\tilde{p}}_x(T(\text{u};\text{ϕ}))]+const.\text{\hspace{1em}(18)}$$
　　实际上，我们可以使用基于随机梯度的方法将$\mathcal{L}(\text{θ})$迭代最小化。由于我们将期望重参数化为与基本分布$p_u(\text{u};\text{ψ})$相关，因此我们可以通过蒙特卡洛来获得$\mathcal{L}(\text{θ})$相对于$\text{ϕ}$梯度的无偏估计。特别是，令 { u n } n = 1 N \{\textbf u_n\}^N_{n=1} {un​}n=1N​为从$p_u(\text{u};\text{ψ})$采样的一组样本，$\mathcal{L}(\text{θ})$相对于$\text{ϕ}$梯度可以估计如下：
$${\nabla }_{\text{ϕ}}\mathcal{L}\text{θ}\approx -\frac{1}{N}\sum _{n=1}^N{\nabla }_{\text{ϕ}}log|det{J}_T(\text{u};\text{ϕ})|+{\nabla }_{\text{ϕ}}log{\tilde{p}}_x(T(\text{u};\text{ϕ})).\text{\hspace{1em}(19)}$$
　　类似地，我们可以重参数化$\text{u}$来估计与$\text{ψ}$相关的梯度：
$$\text{u}=T^{\prime }({\text{u}}^{\prime };\text{ψ})where{u}^{\prime }\sim p_{u^{\prime }}({\text{u}}^{\prime }),\text{\hspace{1em}(20)}$$
然后将期望写成与$p_{u^{\prime }}({\text{u}}^{\prime })$相关。但是，由于我们可以等效地将重参数化$T^{\prime }$包含到$T$中，并用$p_{u^{\prime }}({\text{u}}^{\prime })$替换基本分布，因此我们可以假设而不失一般性，即参数$\text{ψ}$是固定的，并且仅用对$\text{ϕ}$进行优化。
　　为了最小化上述反向KL散度，我们需要能够从基本分布$p_u(\text{u};\text{ψ})$中采样，并通过变换$T$及其雅可比行列式进行计算和微分。这意味着我们可以通过最小化反向KL散度来拟合基于flow的模型，即使我们无法评估基本密度或计算逆变换$T^{-1}$。但是，如果我们想评估受过训练的模型的密度，我们将需要这些操作。
　　反向KL散度通常用于变分推断，这是一种贝叶斯推断的近似形式。在这种情况下，目标是计算后验$p_x^{\ast }(\text{x})$，以作为似然函数和先验密度之间的产物。
　　有关flow在变分推断中的应用样例可以参考Rezende and Mohamed (2015); van den Berg et al. (2018); Kingma et al. (2016); Tomczak and Welling (2016); Louizos and Welling (2017)。我们在第6.2.3节中更详细地介绍此主题。
　　反向KL散度的另一个应用是在模型蒸馏的场景：训练一个flow模型，以替换可以进行密度评估但不是很方便的目标模型$p_x^{\ast }(\text{x})$。van den Oord et al. (2018)等人给出了用flow蒸馏的一个示例。 在他们的情况下，不能有效地从目标模型中采样样本，因此它们将其蒸馏成支持快速采样的flow。

2.3.3 Relationship Between Forward and Reverse KL Divergence

基于flow模型的另一种理解方法是将目标$p_x^{\ast }(\text{x})$视为基本分布，逆flow则作为分布$p_u^{\ast }(\text{u};\text{ϕ})$的推导。直觉上，$p_u^{\ast }(\text{u};\text{ϕ})$是通过$T^{-1}$变换时训练数据将遵循的分布。由于目标和基本分布在给定它们之间变换的情况下，彼此唯一确定，因此，$p_u^{\ast }(\text{u};\text{ϕ})=p_u(\text{u};\text{ψ})$，仅且仅当${\text{p}}_x^{\ast }(\text{x})=p_x(\text{x};\text{θ})$。因此，将模型$p_x(\text{x};\text{θ})$拟合到目标${\text{p}}_x^{\ast }(\text{x})$，可以等价为将推导分布$p_u^{\ast }(\text{u};\text{ϕ})$拟合到基础$p_u(\text{u};\text{ψ})$中。
　　我们现在可能会问：将$p_x(\text{x};\text{θ})$拟合到目标分布与将$p_u^{\ast }(\text{u};\text{ϕ})$拟合到基本分布有何关系？使用变量变换，我们可以得到以下等式（有关详细信息，请参见附录A）：
$$D_{KL}[p_x^{\ast }(\text{x})||p_x(\text{x}|\text{θ})]=D_{KL}[p_u^{\ast }(\text{u};\text{ϕ})||p_u(\text{u};\text{ψ})].\text{\hspace{1em}(21)}$$
　　上述等式说明，使用正向KL散度（最大似然）将模型拟合到目标等同于通过反向KL散度将推导分布$p_u^{\ast }(\text{u};\text{ϕ})$拟合到基本分布$p_u(\text{u};\text{ψ})$。在附录中，我们还表明：
$$D_{KL}[p_x(\text{x};\theta )||p_x^{\ast }(\text{x})]=D_{KL}[p_u(\text{u};\text{ψ})||p_u^{\ast }(\text{u};\text{ϕ})],\text{\hspace{1em}(22)}$$
这意味着通过反向KL散度将模型拟合到目标分布等同于通过正向KL散度（最大似然）将推导分布$p_u^{\ast }(\text{u};\text{ϕ})$拟合到基本分布$p_u(\text{u};\text{ψ})$。

2.3.4 Alternative Divergences

flow模型参数的学习不限于使用KL散度。分布之间差异的测量有许多替代的方法。这些替代方案通常分为两个通用类别，f-divergences使用密度比进行比较，integral probability metrics(IPMs)使用差值进行比较：
$$f-divergence{D}_f[p_x^{\ast }(x)||p_x(\text{x};\text{θ})]={\mathbb{E}}_{p_x(\text{x};\text{θ})}[f(\frac{p_x^{\ast }(\text{x})}{p_x(\text{x};\text{θ})})]\text{\hspace{1em}(23)}$$
$$IPM{\delta }_s[p_x^{\ast }(x)||p_x(\text{x};\text{θ})]={\mathbb{E}}_{p_x^{\ast }(\text{x})}[s(\text{x})]-{\mathbb{E}}_{p_x(\text{x};\text{θ})}[s(\text{x})].\text{\hspace{1em}(24)}$$
　　对于f-divergences，函数$f$为凸函数，当此函数为$f(r)=rlogr$时，则恢复为KL散度。对于IPM，可以从一组测试统计数据中选择该函数$s$，也可以是对抗选择的witness函数。
　　无论先前的KL散度以及当前可选的散度都需考虑：我们是否可以从模型$p_x(\text{x};\text{θ})$中仿真，我们是否知道乘法常数的真实分布，我们是否可以使用该分布的变换或其逆变换？ 在考虑这些散度时，我们会看到基于flow的模型（其设计原理都使用组合和变量变化）与更通用的隐式概率模型类别之间的联系。如果我们选择生成对抗网络的生成器作为归一化流，则可以使用对抗训练，Wasserstein损失或其他方法来训练flow参数。

2.4 Brief Historical Overview

Whitening transformations（将数据转化为白噪声）是在机器学习中使用normalizing flows的前身。Chen and Gopinath (2000) 是第一个使用白化作为密度估计技术而不是用于特征预处理的工作，其被称为Gaussianization。Tabak and Vanden-Eijnden (2010) 从扩散过程的角度进行了高斯化，并与统计力学建立了连接，特别是使用刘维尔方程来表征flow。在后续论文中，Tabak and Turner (2013) 引入了可以将其视为normalizing flows现代概念的内容：引入术语normalizing flows并将flow定义为$K$个简单映射的组合。正如我们将在第3节中讨论的那样，这种可组合的定义对于Flow模型在保留计算和分析能力的同时，也具有丰富表达能力是至关重要的。
　　组合链的想法最初在机器学习中出现是Rippel and Adams (2013)这一工作，他们认识到具有深层神经网络的参数化flow可能会导致相当通用和丰富表示的分布。Dinh et al. (2015) 随后引入了可扩展且计算高效的架构，在图像建模和推理上取得了进一步改进。Rezende and Mohamed (2015) 使用 Tabak and Turner (2013) 的想法和语言在变分推段的设置中应用normalizing flows。此后，正如这里回顾的论文将显示的那样，normalizing flows 现在已经具有大量的文献，这些大量的工作扩大了flow的适用性和可扩展性。
　　由于与变量变换有关，我们还可以将机器学习中normalizing flows的使用与许多其他领域中的历史联系起来。在统计力学的发展中，对度量的变化进行了深入研究，一个著名的例子是上述的刘维尔定理。Copulas可以看作是基本的flow，其中每个维度都使用经验估计的边源累积分布函数独立变换。最优运输（Optimal transport）和Wasserstein度量也可以根据度量的转换来制定（也称为Monge Problem）。特别是，三角映射（与自回归flow有关的概念）可以证明是对一类Monge–Kantorovich问题的约束解决方案。这类三角映射本身具有悠久的历史，Rosenblatt (1952) 研究了它们的特性，以统一地在超立方体上变换多元分布。最佳传输本身就是一个tutorial，因此我们主要避开了这个框架，而是选择考虑变量变化。

3.Constructing Flows Part I: Finite Compositions

　　在描述了flow的一些高级属性和用途之后，我们接下来将描述，分类和统一构造flow的各种方式。如第2.1节所述，normalizing flows是可以组合的。也就是说，我们可以通过组合有限数量的简单变换$T_k$来构造带有变换$T$的flow，如下所示：
$$T=T_K◦\cdots ◦T_1.\text{\hspace{1em}(25)}$$
　　想法是使用简单的变换作为构建块（每个块具有简单的逆变换和雅可比行列式）来定义具有丰富表达能力的复杂变换。重要的是，flow的前向和逆向评估以及雅可比行列式的计算可以定位到单个块（sub-flow）。如图2所示，假设${\text{z}}_0=\text{u}$和${\text{z}}_K=\text{x}$，正向评估是：
$${\text{z}}_k=T_k({\text{z}}_{k-1})fork=1,...,K,\text{\hspace{1em}(26)}$$
逆向评估是：
$${\text{z}}_{k-1}=T_k^{-1}({\text{z}}_k)fork=K,...,1,\text{\hspace{1em}(27)}$$
而且雅可比行列式计算（对数域）为：
$$log|det{J}_T({\text{z}}_0)|=log|\prod _{k=1}^{K}det{J}_{T_k}({\text{z}}_{k-1})|=\sum _{k=1}^{K}log|det{J}_{T_k}({\text{z}}_{k-1})|.\text{\hspace{1em}(28)}$$
　　增加变换的“深度”（即sub-flow的数目）将导致计算复杂性$\mathcal{O}(K)$的增长，这是能够增加表达能力需要支付的成本。
　　在实践中，我们使用具有参数${\varphi }_k$的模型（例如神经网络）来实现$T_k$或$T_k^{-1}$，并将其表示为$f_{{\varphi }_k}$。也就是说，我们可以采用模型$f_{{\varphi }_k}$实现$T_k$，在这种情况下，它以${\text{z}}_{k-1}$作为输入并输出${\text{z}}_k$（或实现$T_k^{-1}$，在这种情况下，它以${\text{z}}_k$作为输入并输出${\text{z}}_{k-1}$）。无论哪种情况，我们都必须确保模型可逆，并且其雅可比行列式容易计算。在本节的其余部分中，我们将描述几种构建$f_{{\varphi }_k}$的方法，以便满足这些要求。表1显示了本节中讨论的所有方法的概述。

　　确保$f_{{\varphi }_k}$可逆和其逆能够显示计算不是一个同义词。在许多实现中，即使能保证存在$f_{{\varphi }_k}$的逆，其逆的计算也可能是昂贵甚至是棘手的。如第2节所述，当采样时使用正向变换$T$，当进行密度评估时则使用逆向变换$T^{-1}$。如果$f_{{\varphi }_k}$的逆不是高效的，则密度评估或采样将导致效率低下甚至是棘手的。$f_{{\varphi }_k}$是否应设计为具有高效的逆，以及是否应采取$T_k$或$T_k^{-1}$的实现是由用法来决定的。
　　我们还应该阐明“雅可比行列式容易计算”的含义。我们可以使用$D$遍前向或逆向自动微分，以计算具有$D$维输入和$D$维输出的可微分函数的雅可比矩阵。然后，我们可以显式计算该雅可比矩阵的行列式。但是，该计算的时间成本为$\mathcal{O}(D^3)$，当$D$很大时是非常棘手的。对于大多数基于flow的模型的应用，雅可比行列式的计算最多应为$\mathcal{O}(D)$。因此，在以下各节中，我们将描述允许雅各布行列式相对于输入维度在线性时间完成计算的函数形式。
　　为了简化符号，我们将删除模型参数对$k$的依赖性，并用$f_{\varphi }$表示模型。另外，无论该模型是实现$T_k$还是$T_k^{-1}$，我们都将模型的输入表示为$\text{z}$，输出表示为${\text{z}}^{\prime }$。

3.1 Autoregressive Flows

　　自回归flow是首先被提出的第一类flow之一，并且仍然是最受欢迎的flow之一。在第2.2节中，我们看到，在较软的条件下，我们可以使用具有三角雅可比矩阵的映射将任何分布$p_x(\text{x})$转化为$(0,1{)}^D$中的均匀分布。自回归flow是该结构的一种直接实现，指定$f_{\varphi }$具有以下形式：
$$z_i^{\prime }=\tau (z_i,{\text{h}}_i)where{\text{h}}_i=c_i({\text{z}}_{<i}),\text{\hspace{1em}(29)}$$
其中$\tau$称为变换器，而$c_i$则是第$i$个调节器，这在图3a中进行了说明。变换器对$z_i$是一个严格单调的函数（因此可逆），并且由${\text{h}}_i$参数化，同时指定flow如何对$z_i$进行操作以输出$z_i^{\prime }$。调节器确定了变换器的参数，进而可以修改变换器的行为。调节器不需要进行双向映射，因为它的一个约束是，第$i$个调节器只能将维度小于$i$的变量作为输入。此时，$f_{\varphi }$的参数$\varphi$通常是调节器的参数，但有时变换器也有其自己的参数（即除了${\text{h}}_i$之外的参数）。
　　只要变换器可逆，那么就可以认为对于任何$\tau$和$c_i$的选择，上述构造都是可逆的。给定$z^{\prime }$，我们可以按以下方式迭代计算$z$：
$$z_i={\tau }^{-1}(z_i^{\prime },{\text{h}}_i)where{\text{h}}_i=c_i({\text{z}}_{<i}).\text{\hspace{1em}(30)}$$
　　这在图3b中进行了说明。在forward计算中，每个${\text{h}}_i$和$z_i^{\prime }$都可以按任何顺序或并行地独立计算。但是，在 invers计算中，所有${\text{z}}_{<i}$都需要在$z_i$之前进行计算，因此${\text{z}}_{<i}$作为用于计算${\text{h}}_i$的调节剂。
　　同样很容易地表明，上述变换的雅可比矩阵是三角形的，因此雅各布行列式是易计算的。由于每个$z_i^{\prime }$不依赖于${\text{z}}_{>i}$，因此每当$j>i$时，$z_i^{\prime }$对$z_j$的偏导数为零。因此，可以以以下形式写出$f_{\varphi }$的雅可比矩阵：
$$J_{f_{\varphi }}(\text{z})=\left[\begin{array}{ccc}\frac{\partial \tau }{\partial z_1}(z_1;{\text{h}}_1)& & \text{0}\\ & \ddots & \\ \text{L}(\text{z})& & \frac{\partial \tau }{\partial z_D}(z_D;{\text{h}}_D)\end{array}\right].\text{\hspace{1em}(31)}$$
　　上述雅可比矩阵是下三角矩阵，其对角线元素是变换器对$\text{z}$的每个元素的偏导数。由于任何三角矩阵的行列式都等于其对角线元素的乘积，因此可以在$\mathcal{O}(D)$时间复杂度内计算$J_{f_{\varphi }}(\text{z})$的对数绝对值行列式，如下所示：
$$log|det{J}_{f_{\varphi }(\text{z})}|=log|\prod _{i=1}^D\frac{\partial \tau }{\partial z_i}(z_i;{\text{h}}_i)|=\sum _{i=1}^{D}log|\frac{\partial \tau }{\partial z_i}(z_i;{\text{h}}_i)|.\text{\hspace{1em}(32)}$$
雅可比矩阵的下三角形部分（在这里用$\text{L}(\text{z})$表示）是无关的。变换器的偏导数可以根据实现方式来计算。
　　自回归flow是一种通用近似器（在第2.2节中讨论的条件下），当变换器和调节器足够灵活时，可以很好地表示任何函数。这是基于2.2节中遵循的通用变换假设，即基于条件性的累积分布函数是自回归flow。但是，这只是表示能力的声明，在实际情况中无法保证flow的行为。
　　自回归flow的一种可替代但在数学上等效的形式，是将调节器$c_i$以${\text{z}}_{<i}^{\prime }$作为输入而不是${\text{z}}_{<i}$。这等同于在上述公式中用${\tau }^{-1}$替换$\tau$，用${\text{z}}^{\prime }$替换$\text{z}$。 两种表述在文献中都是常见的。不失一般性，我们使用${\text{z}}_{<i}$作为$c_i$的输入。有关这两种替代方案之间的计算差异可参考Kingma et al. (2016); Papamakarios et al. (2017)。
　　实现一个自回归flow可以总结为：（a）变换器$\tau$的实现；（b）调节器$c_i$的实现。这些实现都是独立选择的：任何类型的变换器都可以与任何类型的调节器配对，从而产生文献中出现的各种组合。在以下段落中，我们将列出许多变换器的实现（第3.1.1节）和许多调节器的实现（第3.1.2节）。 然后，我们将讨论他们的利弊，并指出文献中特定实现的组合。

3.1.1 Implementing the Transformer

　　（1）Affine transformers
　　affine transformers是变换器最简单的选择之一，也是被首先应用的，其形式如下：
τ ( z i ; h i ) = α i z i + β i w h e r e h i = { α i , β i } . (33) \tau(z_i;\textbf h_i)=\alpha_i z_i+\beta_i\quad where\quad \textbf h_i=\{\alpha_i,\beta_i\}.\tag{33} τ(zi​;hi​)=αi​zi​+βi​wherehi​={αi​,βi​}.(33)
上述变换可以视为位置尺度变换，其中${\alpha }_i$控制尺度，${\beta }_i$控制位置。如果${\alpha }_i\ne 0$，则可以保证可逆性。并且可以令${\alpha }_i=exp{\tilde{\alpha }}_i$（其中${\tilde{\alpha }}_i$是一个无约束参数，且 h i = { α ~ i , β i } \textbf h_i=\{\tilde α_i,β_i\} hi​={α~i​,βi​}）使雅可比行列式容易计算。由于变换器对$z_i$的偏导数等于${\alpha }_i$。因此，对数绝对值雅可比行列式为：
$$log|det{J}_{f_{\varphi }}(\text{z})|=\sum _{i=1}^{D}log|{\alpha }_i|=\sum _{i=1}^D{\tilde{\alpha }}_i.\text{\hspace{1em}(34)}$$
　　具有affine transformers的自回归flow由于其简单性和易分析性而具有很大吸引力，但其表示能力是有限的。为了说明为什么，假设$\text{z}$遵循高斯分布；然后，以${\text{z}}_{<i}^{\prime }$为条件的$z_i^{\prime }$也将遵循高斯分布。换句话说，多元高斯的单个仿射自回归变换导致其条件分布$p_{z^{\prime }}(z_i^{\prime }|{\text{z}}_{<i}^{\prime })$必然也是高斯的。尽管如此，仍然可以通过堆叠多个仿射自回归层来获得强大的表现力，但是尚不清楚具有多少层的仿射自回归flow才能是一个通用近似器。affine transformers在文献中很受欢迎，它已用于诸如NICE，REAL NVP，IAF，MAF和GLOW之类的模型中。
　　（2）Combination-based transformers
　　基于单调函数的组合也是单调的这一观察结果，可以通过简单的组合来构建Non-affine transformers。给定真实变量z的单调函数${\tau }_1,...,{\tau }_K$，下列函数同样是单调的：

• Conic combination：$\tau (z)={\sum }_{k=1}^K{w}_k{\tau }_k(z)$，其中对于所有的$k$，有$w_k>0$。
• Composition：$\tau (z)={\tau }_K◦\cdots ◦{\tau }_1(z)$。

例如，可以使用单调递增激活函数$\sigma (\cdot )$的conic combination来构建non-affine transformer（例如Logistic Sigmoid，Tanh，Leaky Relu等）：
τ ( z i ; h i ) = w i 0 + ∑ k = 1 K w i k σ ( α i k z i + β i k ) w h e r e h i = { w i 0 , . . . , w i k , α i k , β i k } , (35) \tau(z_i;\textbf h_i)=w_{i0}+\sum^K_{k=1}w_{ik}\sigma(\alpha_{ik}z_i+\beta_{ik})\quad where\quad \textbf h_i=\{w_{i0},...,w_{ik},\alpha_{ik},\beta_{ik}\},\tag{35} τ(zi​;hi​)=wi0​+k=1∑K​wik​σ(αik​zi​+βik​)wherehi​={wi0​,...,wik​,αik​,βik​},(35)
对于所有$k\ge 1$，有${\alpha }_{ik}>0$和$w_{ik}>0$。显然，上述构造对应一个单调的单层感知。通过反复组合单调激活函数，我们可以构建一个单调的多层感知器，前提是其所有权重严格为正。
　　上述的变换器可以任意地表示任何单调函数，这与多层感知器的通用近似能力有关（有关详细信息，请参见Huang et al., 2018）。计算变换器雅可比行列式所需的偏导数原则上是可分析的，但更常见的是，它们是通过反向传播来计算。combination-based transformers的缺点是，通常不能分析它们的逆，并且只能迭代地进行逆变换，例如使用bisection搜索。combination-based transformers的变体已用于NAF，Block-NAF和Flow ++等模型中。
　　（3）Integration-based transformers
　　定义non-affine变换器的另一种方法是使用积分变换器，其灵感来自于正函数的积分是单调递增的函数。例如，Wehenkel and Louppe (2019) 将变换器定义为：
τ ( z i ; h i ) = ∫ 0 z i g ( z ; α i ) d z + β i w h e r e h i = { α i , β i } , (36) \tau(z_i;\textbf h_i)=\int^{z_i}_0g(z;\textbf α_i)dz+\beta_i\quad where\quad \textbf h_i=\{\textbf α_i,\beta_i\},\tag{36} τ(zi​;hi​)=∫0zi​​g(z;αi​)dz+βi​wherehi​={αi​,βi​},(36)
其中$g(\cdot ;{\text{α}}_i)$可以是由${\text{α}}_i$参数化的任何正值神经网络。通常，除${\text{α}}_i$外，$g(\cdot ;{\text{α}}_i)$还将具有其自身的参数。计算雅可比行列式中所需变换器的导数等于$g(z_i;{\text{α}}_i)$。这种方法能产生非常灵活的变换器，但积分方法难以进行分析。一种可能是采用数值近似。
　　可以通过将$g(\cdot ;{\text{α}}_i)$定义为正的$2L$次多项式来获得可分析的积分变换器。积分是$z_i$的$2L+1$次多项式，因此可以通过分析进行计算。由于每个正的$2L$次多项式可以写成$L$次多项式平方和，因此可以利用这一定理来定义sum-of-squares polynomial 变换器：
$$\tau (z_i;{\text{h}}_i)={\int }_0^{z_i}\sum _{k=1}^K(\sum _{l=0}^L{\alpha }_{ikl}{z}^l{)}^{2}dz+{\beta }_i,\text{\hspace{1em}(37)}$$
其中${\text{h}}_i$包含${\beta }_i$和所有多项式系数${\alpha }_{ikl}$，并且$K\ge 2$。此外，affine变换器可以作为$L=0$的特殊情况得到：
$${\int }_0^{z_i}\sum _{k=1}^K({\alpha }_{ik0}{z}^0{)}^{2}dz+{\beta }_i=(\sum _{k=1}^K{\alpha }_{ik0}^2)z{|}_0^{z_i}+{\beta }_i={\alpha }_i{z}_i+{\beta }_i,\text{\hspace{1em}(38)}$$
其中${\alpha }_i={\sum }_{k=1}^K{\alpha }_{ik0}^2$。可以证明的是，对于足够大的L，平方和多项式变换器可以近似任何单调递增的函数。尽管如此，由于只能通过分析求解次数最多为4的多项式，因此平方和多项式在$L\ge 2$的情况下，是不可逆的，并且只能使用例如bisection搜索的方法，迭代进行求逆。
　　（4）Spline-based transformers
　　到目前为止，我们已经讨论了各种灵活的non-affine变换器，但是这些变换器无法进行可逆分析。克服此限制的一种方法是将变换器作为单调spline来实现，即由$K$个段组成的分段函数，其中每个段都是一个可逆的简单函数。具体而言，给定$K+1$个输入位置$z_{i0},...,z_{iK}$且每个段在点$z_{i1},...,z_{i(K-1)}$处相接，则在每个区间$[z_{i(k-1)},z_{ik}]$中，变换器$\tau (z_i;{\text{h}}_i)$可被视为一个简单的单调函数（例如，低次多项式）。在区间$[z_{i0},z_{ik}]$之外，变换器默认作为一个简单函数，例如identity函数。通常，变换器的参数${\text{h}}_i$是输入位置$z_{i0},...,z_{iK}$，及其对应的输出位置$z_{i0}^{\prime },...,z_{iK}^{\prime }$，还有点$z_{i_0},...,z_{iK}$处的导数（即斜率，取决于spline的类型）。有关描述，请参见图4。
　　基于spline的变换器由使用的spline类型（即段的函数形式）来区分。 到目前为止，已经探索了以下选择，按照灵活性的增加依次为：线性和二次spline，立方spline，线性有理spline和二次有理spline。基于spline的变换器的逆与评估一样快，同时保持精确的可逆分析。对基于spline的变换器进行评估或求逆首先定位正确的段，这可以使用binary search在$\mathcal{O}(logK)$时间内完成，然后对该段进行评估或求逆，这是容易分析的。通过增加片段$K$的数量，可以增加变换器的灵活性。

3.1.2 Implementing the Conditioner

　　调节器$c_i({\text{z}}_{<i})$可以是${\text{z}}_{<i}$的任何函数，这意味着每个调节器在原则上都可以实现为以${\text{z}}_{<i}$作为输入，并输出${\text{h}}_i$的任意模型。但是，调节器的简单实现是为$D$个维度单独构建独立的模型，这要求进行$D$次模型评估，每个模型都具有平均大小$D/2$的向量。这需要额外存储和评估$D$个独立模型的参数。实际上，早期的flow工作认为自回归方法非常昂贵。
　　但是，可以通过在调节器$c_i({\text{z}}_{<i})$上共享参数，甚至通过将调节器组合到单个模型中来有效解决此问题。在以下段落中，我们将讨论调节器的一些实际实现，以使其扩展到高维度。
　　（1）Recurrent conditioners
　　调节器共享参数的一种方法是使用循环神经网络（RNN）共同实现它们。第$i$个调节器的实现为：
$${\text{h}}_i=c({\text{s}}_i)where\begin{array}{c}{\text{s}}_1=initialstate\\ {\text{s}}_i=RNN(z_{i-1},{\text{s}}_{i-1})fori>1.\end{array}\text{\hspace{1em}(39)}$$
　　RNN一次处理${\text{z}}_{<D}=(z_1,...,z_{D-1})$中的一个元素，在每个步骤中，它都会更新一个具有固定维度的内部状态$s_i$，该状态对子序列${\text{z}}_{<i}=(z_1,...,z_{i-1})$进行了总结。基于${\text{s}}_i$计算${\text{h}}_i$的网络$c$对于每一步都是相同的。初始状态${\text{s}}_1$可以是固定的，也可以是RNN的可学习参数。这里可以使用任何RNN架构，例如LSTM或GRU。
　　RNN在自回归模型的条件分布被广泛使用。基于RNN的自回归模型的示例包括分布估计器，序列模型和图像/视频模型。第3.1.3节讨论了自回归模型与自回归flow之间的关系。
　　在自回归flow的文献中，基于RNN的调节器由Oliva et al. (2018)和Kingma et al. (2016)提出，但与替代方案相比并不常见。基于RNN的调节器的主要缺点是它们将固有的并行计算转换为一个顺序计算：即使可以独立并行计算每个${\text{h}}_i$，也必须基于状态$s_1,...,s_D$顺序计算。由于此循环计算涉及$\mathcal{O}(D)$个步骤，因此对于图像或视频等高维数据可能会很慢。
　　（2）Masked conditioners
　　另一种在调节器之间共享参数但能避免RNN顺序计算的方法是masking调节器。该方法使用单个前馈神经网络，该神经网络接收$\text{z}$并同时输出整个序列$({\text{h}}_1,...,{\text{h}}_D)$。唯一的要求是，该网络必须遵守调节器的自回归结构，即输出${\text{h}}_i$不能取决于输入$z_{\ge i}$。
　　为了构建这样的网络，一种方法是采用任意神经网络并删除相关连接，直到没有输入$z_i$到输出$({\text{h}}_1,\dots ,{\text{h}}_i)$的路径。删除连接的一种简单方法是将每个权重矩阵元素乘以相同大小的二进制矩阵。这具有删除与零权重相对应连接的效果，同时使所有其他连接都没有修改。这个二进制矩阵可以被认为是“屏蔽”了连接。被屏蔽的网络将具有与原始网络相同的架构和大小。反过来，它保留了原始网络的计算属性，例如并行性或在GPU上有效评估的能力。
　　Germain et al. (2015) 提出了一种用于在具有任意隐藏层或隐藏单元的多层感知器上进行mask的通用方法。其关键想法是为每个输入，隐藏和输出单元分配一个$1$和$D$之间的度，并屏蔽层之间的权重，以便没有单元馈入具有较低或相等度的单元。在卷积网络中，可以通过用相同大小的二进制矩阵乘以滤波器来完成屏蔽，从而得到一种通常称为自回归或因果卷积的卷积类型。在使用自注意力的体系结构中，可以通过归零softmax概率来完成屏蔽。
　　屏蔽自回归flow具有两个主要优势。首先，它们能进行高效评估。给定$\text{z}$，可以对神经网络进行一次forward来获得参数$({\text{h}}_1,...,{\text{h}}_D)$，然后可以通过$z_i^{\prime }=\tau (z_i;{\text{h}}_i)$并行计算$z^{\prime }$的每个维度。其次，屏蔽自回归flow是一个通用近似器。给定足够大的调节器和足够灵活的变换器，它们可以用单调变换器表示任何自回归变换，从而在任意两个分布之间进行转换（如第2.2节所述）。
　　另一方面，屏蔽自回归flow的主要缺点是它们的逆不像评估那样高效。这是因为计算$z_i={\tau }^{-1}(z_i^{\prime };{\text{h}}_i)$所需的参数${\text{h}}_i$，在获得所有$(z_i,\dots ,z_{i-1})$之前都无法计算。遵循此逻辑，我们必须首先计算${\text{h}}_1$并得到$z_1$，然后计算${\text{h}}_2$来得到$z_2$，依此类推，直到获得$z_D$为止。使用屏蔽调节器$c$，可以在伪代码中实现上述过程，如下所示：
$$\begin{array}{rl}& Initialize\text{z}toanarbitraryvalue\\ & fori=1,...D\\ & ({\text{h}}_1,...,{\text{h}}_D)=c(\text{z})\\ & z_i={\tau }^{-1}(z_i^{\prime };{\text{h}}_i).\end{array}\text{\hspace{1em}(40)}$$
　　为了明白为什么此过程是正确的，观察到如果${\text{z}}_{\le i-1}$在第$i$次迭代之前是正确的，那么${\text{h}}_i$将被正确计算（由于$c$的自回归结构），因此在第$(i+1)$次迭代之前，${\text{z}}_{\le i}$将是正确的。由于${\text{z}}_{\le 0}=\varnothing$在第一次迭代之前是正确的（在退化的意义上），因此，通过归纳，${\text{z}}_{\le D}=\text{z}$在循环结束时将是正确的。即使上述过程可以准确地求逆flow（前提是变换器易逆），它仍需要调用调节器$D$次。这意味着，使用上述方法对屏蔽自回归flow求逆要比评估正向变换耗时。对于高维数据，例如图像或视频，这可能非常昂贵。
　　Song et al. (2019) 提出的一种对flow求逆的替代方法，其通过迭代下式 Newton-style 固定点更新来求解方程${\text{z}}^{\prime }=f_{\varphi }(\text{z})$：
$${\text{z}}_{k+1}={\text{z}}_k-\alpha diag(J_{f_{\varphi }}({\text{z}}_k){)}^{-1}(f_{\varphi }({\text{z}}_k)-{\text{z}}^{\prime }),\text{\hspace{1em}(41)}$$
其中$\alpha$是一个步长超参数，$diag(\cdot )$返回一个对角矩阵，其对角线元素与其输入相同，且初始化${\text{z}}_0={\text{z}}^{\prime }$。Song et al. (2019)表明，上述过程在$0<\alpha <2$时局部收敛，并且由于$f_{\varphi }^{-1}({\text{z}}^{\prime })$是唯一的固定点，因此该过程必须收敛或多样化。通过屏蔽自回归flow，可以通过调用调节器一次来高效地计算$f_{\varphi }({\text{z}}_k)$和$diag(J_{f_{\varphi }}({\text{z}}_k))$。因此，上述Newton-like过程在实践中的迭代次数明显小于$D$。另一方面，上述Newton-like过程是近似的，并且保证仅在局部收敛。
　　尽管与逆相关的计算很困难，masking仍然是实现自回归flow的最受欢迎的技术之一。它非常适合不需要求逆或数据维度不太大的情况。使用屏蔽flow的模型包括IAF，MAF，NAF，Block-NAF，MintNet和MaCow。masking同样在非flow的自回归模型中很受欢迎（例如MADE，PixelCNN和WaveNet）。
　　（3）Coupling layers
　　正如我们已经看到的，屏蔽自回归flow会面临影响其应用和可用性的计算不对称性。采样或密度评估要比另一个慢$D$倍。如果这两个操作都需要快速进行，则需要对调节器进行不同的实现。一种计算对称性（即评估和求逆一样快）的实现是 coupling layer。这个想法是选择一个索引$d$（常见的选择是使用$D/2$并近似到整数）并设计如下的调节器：

• 参数$({\text{h}}_1,...,{\text{h}}_d)$是常数，即不是$\text{z}$的函数。
• 参数$({\text{h}}_{d+1},...,{\text{h}}_D)$是${\text{z}}_{\le d}$的函数，即它们不依赖于${\text{z}}_{>d}$。

这可以使用任意函数近似器$F$（例如神经网络）轻松实现这一点，例如：
$$\begin{array}{c}({\text{h}}_1,...,{\text{h}}_d)=constants,eitherfixedorestimated\\ ({\text{h}}_{d+1},...,{\text{h}}_D)=F({\text{z}}_{\le d}).\end{array}\text{\hspace{1em}(42)}$$
　　换句话说，耦合层将$\text{z}$分为两个部分，例如$\text{z}=[{\text{z}}_{\le d},{\text{z}}_{>d}]$。第一部分是独立于其他维度进行逐元素变换。第二部分以取决于第一部分的方式进行逐元素变换。我们还可以将耦合层视为一种激进屏蔽策略的实现，该策略仅允许$({\text{h}}_{d+1},...,{\text{h}}_D)$仅取决于${\text{z}}_{\le d}$。
　　耦合层的常见实现固定变换器$\tau (\cdot ;{\text{h}}_1),...,\tau (\cdot ;{\text{h}}_d)$为恒等函数。在这种情况下，转换可以写成下式：
$$\begin{array}{c}{\text{z}}_{\le d}^{\prime }={\text{z}}_{\le d}\\ ({\text{h}}_{d+1},...,{\text{h}}_D)=F({\text{z}}_{\le d}).\\ z_i^{\prime }=\tau ({\text{z}}_i;{\text{h}}_i)fori>d.\end{array}\text{\hspace{1em}(43)}$$
反过来，逆变换很简单，由以下方式给出：
$$\begin{array}{c}{\text{z}}_{\le d}={\text{z}}_{\le d}^{\prime }\\ ({\text{h}}_{d+1},...,{\text{h}}_D)=F({\text{z}}_{\le d}).\\ z_i^{\prime }={\tau }^{-1}({\text{z}}_i;{\text{h}}_i)fori>d.\end{array}.\text{\hspace{1em}(44)}$$
上述过程如图5所示。与所有自回归flow一样，变换的雅可比矩阵是下三角矩阵，此外，它还具有以下特殊结构：
$$J_{f_{\varphi }}=\left[\begin{array}{cc}\text{I}& \text{0}\\ \text{A}& \text{D}\end{array}\right],\text{\hspace{1em}(45)}$$
其中，$\text{I}$是一个$d\times d$的恒等矩阵，$\text{0}$是$d\times (D-d)$的零矩阵，$\text{A}$是$(D-d)\times d$的全矩阵，$\text{D}$是一个$(D-d)\times (D-d)$的对角矩阵。此时，雅可比行列式仅仅是$\text{D}$对角元素的乘积，对角元素为变换$\tau (\cdot ;{\text{h}}_{d+1}),...,\tau (\cdot ;{\text{h}}_D)$的导数。
　　耦合层和完全自动回归flow是两种实现的极端。耦合层将$\text{z}$分为两个部分，并将第二部分逐元素的变换作为第一部分的函数，而完全自动回归flow将输入分为$D$个部分（每个部分一个元素），并将每个部分的转换作为先前所有部分的函数。显然，存在一个中间选择：即可以将输入分为$K$部分，并将第$k$部分逐元素的变换作为$1$至$k-1$部分的函数，$k=2$对应于耦合层，$k=D$对应于完全自回旋flow。使用屏蔽调节器，逆变换将比评估慢$\mathcal{O}(K)$倍，因此可以根据任务的计算要求选择$K$。
　　耦合层的高效是以降低表达能力为代价的。与循环或屏蔽自回归flow不同，无论函数$F$的表现力如何，单个耦合层都不可能再代表任何自回归变换。因此，具有单个耦合层的自回归flow不再是通用近似器。但是，可以通过组合多个耦合层来提高flow的表达能力。在组合耦合层时，需要在层之间排列$\text{z}$的元素，以便所有维度都有机会进行变换以及交互。先前工作表明，组合耦合层确实可以创建灵活的flow。
　　从理论上讲，只要第$i$个耦合层的索引$d$等于$l-1$，就可以很容易地表明$D$个耦合层的组合确实是通用近似器。观察到第$i$个耦合层可以表达$z_i^{\prime }=\tau (z_i;c_i(\text{z}<i))$的任何变换，因此$D$个这样的层的组合能够变换每个维度。但是，该结构无论向前还是反向都涉及$D$个序列计算（每一层），因此不会对循环或屏蔽自回归flow带来改进。是否可以通过少于$\mathcal{O}(D)$个耦合层来获得通用近似器，这是一个开放的问题。
　　耦合层是实现基于flow的模型的最流行方法之一，因为它们允许密度评估和采样同样快速。基于耦合层的flow容易与最大似然结合，然后从有效地进行采样。因此，在高维数据的生成模型（例如图像，音频和视频）中经常发现耦合层。带有耦合层的基于flow的模型包括NICE，Real NVP，Glow，WaveGlow，FloWaveNet和Flow++。

3.1.3 Relationship with Autoregressive Models

除了标准化flow外，另一类用于高维分布的模型是自回归模型。自回归模型历史悠久，从贝叶斯网络的通用框架到最新的基于神经网络的实现。
　　为了构建$p_x(\text{x})$的自回归模型，我们首先使用链式法则将$p_x(\text{x})$分解为1维条件概率的乘积：
$$p_x(\text{x})=\prod _{i=1}^D{p}_x(x_i|{\text{x}}_{<i}).\text{\hspace{1em}(46)}$$
　　然后，我们通过使用具有参数${\text{h}}_i$的参数化分布对每个条件分布进行建模：
$$p_x(x_i|{\text{x}}_{<i})=p_x(x_i;{\text{h}}_i),where{\text{h}}_i=c_i({\text{x}}_{<i}).\text{\hspace{1em}(47)}$$
　　例如，$p_x(x_i;{\text{h}}_i)$可以是由均值和方差进行参数化的高斯函数，也可以是通过每个组件的均值，方差和混合系数参数化的混合高斯。函数$c_i$类似于自回归flow的调节剂，并且通常使用RNN或掩屏蔽神经网络实现，如先前部分所述。除了连续数据外，自回归模型可以轻松用于离散甚至混合数据。如果$x_i$对于某些$i$是离散的，则$p_x(x_i;{\text{h}}_i)$可能是参数概率质量函数。
　　现在，我们表明，所有连续变量的自回归模型实际上都是带有单个自回归层的自回归flow。令$\tau (x_i;{\text{h}}_i)$为$p_x(x_i;{\text{h}}_i)$的累积分布函数，定义如下：
$$\tau (x_i;{\text{h}}_i)={\int }_{-\infty }^{x_i}{p}_x(x_i^{\prime };{\text{h}}_i)d{x}_i^{\prime }.\text{\hspace{1em}(48)}$$

3.2 Linear Flows

3.3 Residual Flows

3.4 Practical Considerations when Combining Transformations

4. Constructing Flows Part II: Continuous-Time Transformations

4.1 Definition