Symbolic Discovery of Optimization Algorithms翻译

摘要

我们提出了一种将算法发现形式化为程序搜索的方法，并应用该算法以发现用于深度神经网络训练的优化算法。我们利用高效的搜索技术来探索无限且稀疏的程序空间。为了桥接代理和目标任务之间的巨大泛化差距，我们还引入了程序选择和简化策略。我们的方法发现了一种简单有效的优化算法，即Lion（EvoLved Sign Momentum）。它比Adam在存储上更高效，因为它只对动量部分进行跟踪。与自适应优化器不同，对于通过符号操作计算的每个参数更新，其幅度都是相同的。我们通过在不同任务上训练各种模型，以将Lion与广泛使用的优化器（例如Adam和Adafactor）进行比较。 在图像分类任务上，Lion在ImageNet上提高了ViT 2%的准确性，并节省了高达5倍的JFT训练计算。在视觉语言对比学习上，我们在ImageNet上获得了zero-shot 88.3％和fine-tuning 91.1％的精度，分别超过了先前最佳结果的2％和0.1％。在扩散模型上，Lion优于Adam，其达到最高的FID分数，并减少了2.3倍的计算。对于自回归，屏蔽语言建模和微调，与Adam相比，Lion表现出相似或更好的性能。我们对Lion的分析表明，它的性能增益随训练batch的大小而增长。由于符号函数产生的更新规整较大，它还需要比Adam小的学习率。此外，我们检查了Lion的局限性，并确定了其改进较小或没有统计学意义的场景。Lion的实现目前已公开可用，https://github.com/google/automl/tree/master/lion。

1.介绍

优化算法，即优化器，在训练神经网络中起着基本作用。近年来有大量人工设计的优化器被提出，主要是自适应的优化器。但是，具有解藕权重衰减的Adam（即AdamW），以及使用分解的第二动量的Adafactor仍然是训练大多数深度神经网络的标准优化器，尤其是最近的SOTA语言，视觉和多模态模型。
　另一个方向是自动发现这种优化算法。learning to optimize（L2O）方法提出通过训练参数化模型（例如神经网络）来作为优化器，该模型能输出更新的参数梯度。但是，这些黑盒优化器通常在有限数目的小任务被训练，这很难泛化到更大的模型和更多的训练步数。另一方法采用强化学习或蒙特卡洛采样来发现新的优化器，在该方法中，搜索空间是由预定义的操作数（例如梯度和动量）和操作符（例如一元和二元数学运算）所组成的树定义的。但是，为了使搜索易于管理，它们通常通过使用固定的操作数并限制树的大小来限制搜索空间，从而限制了发现更优优化器的可能性。因此，发现的算法尚未达到SOTA。AutoML-Zero是一个有希望的努力，它试图在评估玩具任务的同时搜索机器学习pipeline中的每个组件。这项工作遵循自动发现优化器的研究方向，尤其是受AutoML-Zero的启发，但旨在发现可以改善最先进基准测试的有效优化算法。
　在本文中，我们提出了一种将算法发现作为程序搜索的方法，并应用其以发现优化算法。目前有两个主要挑战：第一个是在无限且稀疏的程序空间中找到高质量的算法。第二个是进一步选择可以从小型任务推广到更大SOTA任务的算法。为了应对这些挑战，我们采用了一系列技术，包括具有热启动的进化搜索和重启动，abstract execution，funnel selection和程序简化。
　我们的方法发现了一种简单有效的优化算法：Lion， EvoLved Sign Momentum的缩写。该算法不同于各种自适应算法，其仅通过跟踪动量并利用符号操作来计算更新，从而导致较低的内存开销和所有维度均匀的更新幅度。尽管简单，但Lion在各种模型（Transformer，MLP，ResNet，U-Net和Hybrid）和任务（图像分类，视觉语言对比学习，扩散模型，语言建模和微调）上具有出色表现。值得注意的是，我们通过在BASIC中用Lion代替Adafactor，这在ImageNet上实现了88.3％的zero-shot和91.1％的微调精度，分别超过了先前SOTA结果的2％和0.1％。此外，Lion将JFT上的预训练计算最多降低了5倍，将扩散模型的训练效率提高了2.3倍，同时获得了更好的FID分数，并在节省2倍计算存储的语言建模上提供相当或更好的性能。
我们分析Lion的特性和局限性。读者应意识到，使用符号函数计算出的均匀更新与SGD以及自适应方法生成的更新相比，通常会产生更大的范数。因此，Lion需要较小的学习率，以及较大的权重衰减才能保持有效的重量衰减强度。有关详细的指导，请参阅第5节。此外，我们的实验表明，Lion的增益随batch-size而增加，并且与AdamW相比，它对不同的超参数选择更鲁棒。对于局限性，Lion和AdamW之间的差异在某些大规模语言和图像文本数据集上并不显着。如果在训练过程中使用较大的增强或较小的batch（<64），则Lion的优势是较小的。有关详细信息，请参见第6节。

2.Symbolic Discovery of Algorithms

我们提出了一种方法，该方法将算法发现形式化为程序搜索。我们以程序的形式进行符号化表示具有以下优势：（1）它对齐了将算法作为可执行程序进行实现的事实；（2）与神经网络等参数化模型相比，诸如程序之类的符号化表示更容易分析，理解和迁移到新任务；（3）程序长度可用于估计不同程序的复杂性，从而使其更容易去选择简单的，通常更具泛化性的程序。这项工作的重点是用于深神经网络培训的优化器，但该方法通常适用于其他任务。

2.1 Program Search Space

在设计程序搜索空间时，我们遵守以下三个准则：（1）搜索空间应足够灵活，以便发现新的算法；（2）程序应易于分析并可纳入机器学习的工作流程；（3）程序应重点关注高级算法设计，而不是低级实现细节。我们在n维数组上定义了了包含函数操作的程序，包括用命令性语言的列表，以及包含此类数组的字典等结构。它们类似于使用NumPy/JAX的Python代码以及优化算法伪代码。设计的详细信息在下面进行了描述，并在Program 3中给出了一个AdamW的示例表示。
Input / output signature。该程序定义了一个train函数，该函数编码了要搜索的优化算法，其中主要输入是模型在当前训练步骤中的权重（$w$），梯度（$g$）和学习率（$lr$）。主要输出是权重的更新结果。该程序还结合了初始化为零的额外变量，以在训练期间收集历史信息。例如，AdamW需要两个额外的变量来估计第一和第二动量。请注意，这些变量可以任意命名，我们在Program 3使用名称$m$和$v$，只是为了更好的可读性。Program 2中的简化代码片段使用与AdamW相同的函数名，以确保发现的算法具有较小或相等的内存足迹。与以前的优化器搜索尝试相反，我们的方法允许发现更新额外变量的更好方法。
Building block。train函数由一系列赋值命令组成，该函数对命令或局部变量的数量没有限制。每个命令使用常数或现有变量作为输入来调用一个函数，结果值存储在新变量或现有变量中。对于程序，我们选择45个常见的数学函数，其中大多数对应于NumPy中的一个函数或线性代数中的操作。此外引入了一些函数以使程序更紧凑，例如线性插值函数$interp(x,y,a)$，其等效于$(1-a)\ast x+a\ast y$。初步实验研究了包括条件和循环命令等更高级函数，并定义和调用新的函数，但这些函数并未产生改进的结果，因此我们决定将其排除。附录H中总结了函数的详细说明。在必要时，函数参数的类型和大小会自动映射，例如，在将一个数组字典添加到标量的情况下。
Mutations and redundant statements。进化搜索中使用的变异操作与程序的符号化表示能很好的结合起来。我们包括了三种类型的变异操作：（1）在一个随机位置上插入一个新命令，该命令具有随机选择的函数和参数，（2）删除随机选择的命令，（3）通过随机替换函数参数之一来随机修改命令 ，这个参数可能是变量或常数。为了对参数进行变异，我们用一个现有变量或通过从正态分布$X〜\mathcal{N}(0,1)$采样获得的常数进行替换。此外，我们可以通过乘以一个随机因子$2^a,a〜\mathcal{N}(0,1)$，来变异现有常数。这些常数在优化算法中作为可调的超参数，例如AdamW中的峰值学习率和权重衰减。请注意，我们允许程序在搜索过程中包含冗余命令，即不会影响最终程序输出的命令。这是必要的，因为变异仅限于影响单个命令。因此，冗余的命令可以作为未来真实修改的中间步骤。
Infinite and sparse search space。考虑到命令和局部变量的数目是无线的，以及变异常数的存在，程序搜索空间是无限的。即使我们忽略了常数并约束程序的长度和变量数目，潜在程序的数量仍然很大。可能程序的数量粗略估计为$n_p=n_f^l{n}_v^{n_a\ast l}$，其中$n_f$是可能的函数数目，$n_v$是局部变量的数目，$n_a$是每个命令的平均参数数目，$l$是程序长度。更重要的挑战是来自搜索空间中高性能程序的稀疏性。为了说明这一点，我们进行了随机搜索，该搜索在低成本代理任务上评估了超过2M的程序。其中最好的程序仍然不如AdamW。

2.2 Efficient Search Techniques

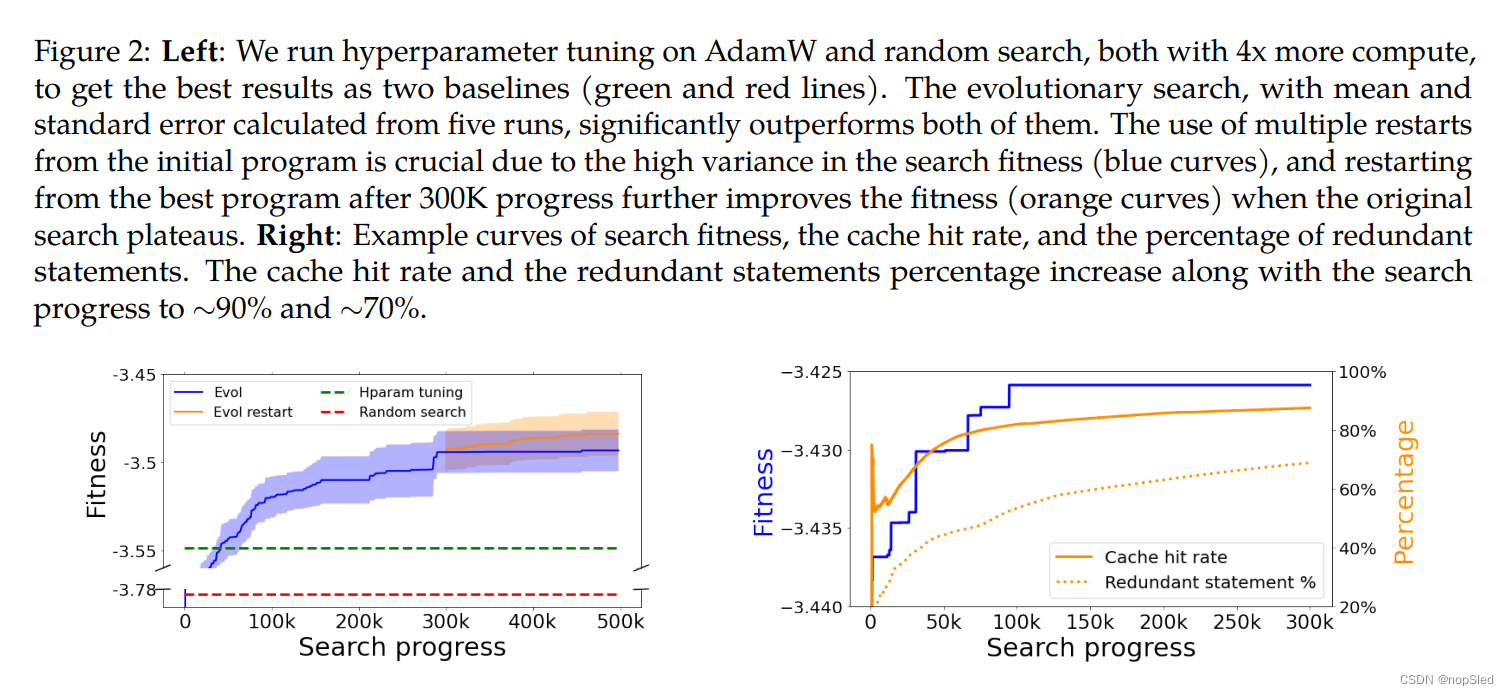
我们采用了以下技术来应对无限和稀疏搜索空间所带来的挑战。
Evolution with warm-start and restart。我们应用了正则化进化，因为它简单，可扩展，并且在许多AutoML搜索任务上都展示了成功。它通过循环逐渐改善$P$算法的种群。每次循环都随机选择$T<P$的算法，同时选择性能最好的算法，以作为父种群，即tournament selection。然后将该父种群复制和变异以产生子种群算法，该算法被添加到种群中，而最老的算法被去除。通常，进化搜索从随机候选种群开始，但我们使用AdamW来热启动初始种群，以加速搜索。默认情况下，我们使用两个比赛，种群大小为1K。 为了进一步提高搜索效率，我们采用了两种重启动方式：（1）从初始程序重新启动，由于进化的随机性并鼓励探索，这可能导致不同的局部最优选择。 这可以通过并行运行多个搜索来完成。（2）从目前发现的最优算法重新开始，以进一步优化它，同时鼓励探索。图2（左）显示了五个进化搜索实验的平均值和标准差。我们通过仅允许进化中的常数进行变异来运行基于AdamW的超参数调整，以及通过采样随机程序进行随机搜索，均需要4倍的计算。 我们的搜索大大优于图中虚线这两个基线所取得的最佳结果。
Pruning through abstract execution。我们提出从三个来源中修剪程序空间的冗余：具有语法或类型/形状错误的程序，功能等效的程序以及程序中的冗余语句。在实际执行程序之前，我们执行一个虚拟执行步骤：（1）输入变量类型和形状以检测错误的程序，并继续变异父程序，直到生成有效的子程序为止；（2）产生一个记录如何从输入计算输出的唯一标识哈希，使我们能够缓存并查找语义重复程序；（3）确定在实际执行和分析过程中可以忽略的冗余语句。例如，在删除Program 8中的所有冗余语句之后，获得了Program 4。与实际执行相比，虚拟执行的成本可忽略不计，每个输入和函数被自定义值替换，例如哈希。有关虚拟执行的详细信息，请参见附录I。初步实验表明，搜索过程可能会被无效的程序所淹没，并且在不滤除无效程序的情况下无法取得进展。如图2（右）所示，随着搜索的进行，冗余命令和缓存命中率的百分比都会增加。基于五次搜索运行，每个都涵盖了300K个程序，最后有69.8±1.9％的冗余语句，这意味着冗余的删除措施使该程序搜索平均缩短了约3倍，因此更易于分析。缓存命中率为89.1±0.6％，表明使用哈希表作为缓存的搜索成本降低了约10倍。
Proxy tasks and search cost。为了降低搜索成本，我们通过减少模型大小，训练样例的数量以及目标任务的训练步骤数来创建低成本代理。对代理的评估可以在20分钟内的一个TPU V2芯片上完成。我们使用验证集上的精度或困惑度来评估。每个搜索实验都使用100个TPU V2芯片，并运行约72H。每个搜索实验期间总共生成了200-300K程序。但是，由于通过虚拟执行使用缓存，实际评估的程序数量约为20-30k。为了合并重启动。有关代理任务的详细信息，请参见附录F。

2.3 Generalization: Program Selection and Simplification