9 传统时间序列模型

平稳性：一个AR模型是平稳的，当且仅当所有模型参数的特征根都在单位圆之外。换句话说，如果模型参数的特征方程 𝜙(𝑧)=1−𝜙1𝑧−𝜙2𝑧2−⋯−𝜙𝑝𝑧𝑝=0ϕ(z)=1−ϕ1z−ϕ2z2−⋯−ϕpzp=0 的所有根的模都大于1，则模型是平稳的。
预测：AR模型的一个重要应用是预测未来值。一旦模型参数被估计出来，就可以使用最近的观测值来预测未来的值。
参数估计：AR模型的参数通常使用最小二乘法或极大似然估计法来估计。

1.1.2 何时使用AR模型

平稳数据：AR模型适用于平稳的时间序列数据，即数据的统计特性（均值、方差等）不随时间改变。
短期预测：由于AR模型依赖于最近的观测值，因此它在短期预测中表现良好。
无明显趋势或季节性：如果时间序列没有明显的长期趋势或季节性模式，AR模型可能是合适的选择。
数据呈现自相关性：如果时间序列显示出自相关性，即当前时刻的值与过去时刻的值之间存在线性关系，那么AR模型可以很好地捕捉这种关系。

1.2 移动平均模型（MA）

移动平均（Moving Average, MA）模型是时间序列分析中另一种重要的工具，它与自回归（AR）模型一起构成了时间序列建模的基础。MA模型假设当前时刻的值与过去一段时间内的误差项（也称为扰动项或白噪声项）有关（这里的“误差项”是指模型在每个时间点上对实际观测值与预期值之间的差异）。这种模型主要用于捕捉序列中的随机波动，并且通常用于短期预测。

白噪声序列是一种特殊的随机过程，在时间序列分析中经常被提及。白噪声序列具有以下几个重要特征：

独立性：白噪声序列中的每个观测值都是相互独立的。
均值：白噪声序列的均值为零。
方差：白噪声序列具有常数方差，通常表示为 𝜎2。
无自相关性：白噪声序列在不同时间点上的观测值之间不存在自相关性

1.2.1 MA模型定义

一个 𝑞 阶的移动平均模型（记作 MA(q)）可以表示为：

𝑦𝑡=𝜇+𝜖𝑡+𝜃1𝜖𝑡−1+𝜃2𝜖𝑡−2+⋯+𝜃𝑞𝜖𝑡−𝑞yt=μ+ϵt+θ1ϵt−1+θ2ϵt−2+⋯+θqϵt−q

其中：

𝑦𝑡 是在时间点 𝑡 的观测值。
𝜇 是序列的均值。
𝜖𝑡 是在时间点 𝑡的白噪声误差项，通常假定为均值为0、方差为 𝜎2的随机变量。
𝜃1,𝜃2,…,𝜃𝑞θ1,θ2,…,θq 是模型的参数，表示过去 𝑞 个时刻误差项的权重。
𝑞 是模型的阶数，即模型中考虑了多少个过去的误差项。

1.2.2 MA模型的性质

平稳性：MA模型总是平稳的，因为它的定义不依赖于过去的观测值，而是依赖于白噪声序列，后者是平稳的。
预测：MA模型的预测是基于最近的误差项，因此它在短期预测中表现良好。
参数估计：MA模型的参数通常使用极大似然估计法来估计。

1.2.3 何时使用MA模型

短期预测：由于MA模型依赖于最近的误差项，因此它在短期预测中表现良好。
平稳数据：MA模型适用于平稳的时间序列数据，即数据的统计特性（均值、方差等）不随时间改变。
随机波动：如果时间序列主要由随机波动组成，而没有明显的趋势或季节性模式，MA模型可能是合适的选择。
数据呈现短期相关性：如果时间序列显示出短期的相关性，即当前时刻的值与过去几个时刻的误差项有关，那么MA模型可以很好地捕捉这种关系。

1.3 ARIMA

ARIMA（Autoregressive Integrated Moving Average，自回归积分滑动平均）模型是时间序列分析中一种非常强大的工具，它可以用来预测具有趋势和季节性的数据。ARIMA模型结合了自回归（AR）、差分（I）、移动平均（MA）三种模型的特性，因此可以处理非平稳数据。

1.3.1 ARIMA模型定义

ARIMA模型的形式化定义如下：

其中：

x𝑡 是在时间点 𝑡 的观测值。
𝑐 是常数项，可以理解为序列的均值。
𝜙1,𝜙2,…,𝜙𝑝ϕ1,ϕ2,…,ϕp 是自回归模型的参数。
𝜃1,𝜃2,…,𝜃𝑞θ1,θ2,…,θq 是移动平均模型的参数(残差项)。
𝜖𝑡ϵt 是白噪声序列，通常假定为均值为0、方差为 𝜎2σ2 的随机变量。

ARIMA模型的组成部分

自回归部分 (AR)：这部分表示当前时刻的观测值与过去若干个时刻的观测值之间的关系。
差分部分 (I)：这部分通过差分来使序列变得平稳。如果序列是非平稳的，通常需要对其进行一次或多次差分处理。
移动平均部分 (MA)：这部分表示当前时刻的观测值与过去一段时间内的误差项之间的关系。

ARIMA模型的表示

ARIMA模型通常用 (𝑝,𝑑,𝑞) 来表示，其中：

𝑝 表示自回归部分的阶数。
𝑑 表示差分的阶数。
𝑞 表示移动平均部分的阶数。

ARIMA模型的应用

非平稳数据：ARIMA模型适用于非平稳数据的分析，通过差分操作可以使序列变得平稳。
短期预测：ARIMA模型可以很好地用于短期预测，尤其是当数据表现出趋势和季节性时。
复杂数据：ARIMA模型可以处理包含趋势和季节性成分的时间序列数据。
多变量时间序列：ARIMA模型也可以扩展到多变量时间序列分析中，如VARIMA模型。

参数选择

在建立ARIMA模型之前，需要确定模型的参数 (𝑝,𝑑,𝑞)(p,d,q)。这通常通过以下步骤完成：

平稳性检验：使用Augmented Dickey-Fuller (ADF) 测试或KPSS测试来检查序列是否平稳。
差分：如果序列是非平稳的，通过差分操作使其变得平稳。差分的阶数 𝑑d 即为需要差分的次数。
自相关函数 (ACF) 和偏自相关函数 (PACF) 图：通过ACF和PACF图来确定 𝑝p 和 𝑞q 的值。
- 对于AR部分，PACF图会在 𝑝p 个滞后期后逐渐衰减到零。
- 对于MA部分，ACF图会在 𝑞q 个滞后期后逐渐衰减到零。

四种基础时间序列模型的应用与结果分析【AR、MA、ARMA、ARIMA】-CSDN博客

2 一指数平滑

指数平滑（Simple Exponential Smoothing, SES），也称为简单指数平滑法，是一种常用的时间序列预测方法。这种方法特别适用于没有明显趋势或季节性模式的数据集。一指数平滑的核心思想是对时间序列的历史数据进行加权平均，其中较新的观测值被赋予更大的权重，而较旧的观测值则被赋予较小的权重。

2.1 指数平滑公式

一指数平滑的计算公式如下：

其中：

𝑦^𝑡+1 是在时间点 𝑡+1的预测值。
𝑦𝑡 是在时间点 𝑡的实际观测值。
𝑦^𝑡是在时间点 𝑡的预测值。
𝛼 是平滑系数（也称为平滑因子），取值范围通常是 0<𝛼<1。

平滑系数 𝛼

平滑系数 𝛼α 控制着新数据对预测值的影响程度：

如果 𝛼 接近 1，则最近的观测值对预测值影响较大，这意味着预测值会快速跟踪实际数据的变化。
如果 𝛼 接近 0，则预测值更依赖于历史数据，对新数据的变化反应较慢。

初始化

在一指数平滑中，需要确定初始预测值 𝑦^1，通常采用的方法有：

将 𝑦1 作为 𝑦^1 的值。
使用序列的平均值。
使用其他合理的方法进行估计。

一指数平滑的步骤

初始化：选择初始预测值 𝑦^1 和平滑系数 𝛼。
更新预测值：对于每个时间点 𝑡，基于当前观测值 𝑦𝑡和之前的预测值 𝑦^𝑡更新预测值 𝑦^𝑡+1。
预测：使用最新的预测值 𝑦^𝑇 预测下一个时间点 𝑇+1的值。

2.2 适用场景

一指数平滑适用于以下情况：

数据不包含明显的趋势或季节性模式。
最近的观测值比早期的观测值更重要。
需要快速响应数据变化的情况。

优点

简单易用。
计算量小。
能够快速适应数据的变化。

缺点

当数据包含趋势或季节性时效果不佳。
过度依赖平滑系数的选择，不同的 𝛼α 值可能导致显著不同的预测结果。

2.3 一指数平滑与自回归模型的主要区别

模型假设：

一指数平滑：假设当前时刻的预测值与最近的观测值相关，并且随着观测值越久远，其影响越小。
自回归模型：假设当前时刻的值与过去若干个时刻的值存在线性关系。

参数：

一指数平滑：只有一个参数，即平滑系数 𝛼α。
自回归模型：有 𝑝p 个参数，即自回归系数 𝜙1,𝜙2,…,𝜙𝑝ϕ1,ϕ2,…,ϕp。

适用场景：

一指数平滑：适用于平稳的时间序列数据，且数据中没有明显的趋势或季节性。
自回归模型：适用于捕捉时间序列中的自相关性，适用于数据中存在趋势或季节性但通过差分处理可以变得平稳的情况。

预测：

一指数平滑：更适合短期预测，因为它依赖于最近的观测值。
自回归模型：可以用于短期和中期预测，因为它考虑了过去的观测值。

计算复杂度：

一指数平滑：计算简单，只需要一个平滑系数。
自回归模型：计算相对复杂，需要估计多个参数。

https://zhuanlan.zhihu.com/p/33322044

3 二指数平滑

二指数平滑（Double Exponential Smoothing, DES），也称为霍尔特方法（Holt's method），是一种用于时间序列预测的技术，主要用于处理具有线性趋势的时间序列数据。该方法通过应用两个平滑过程来捕捉序列中的趋势成分，一个用于平滑水平（类似于一指数平滑），另一个用于平滑趋势。

3.1 二指数平滑的原理

二指数平滑模型由两个部分组成：水平分量（level component）和平滑趋势分量（trend component）。这些分量分别用平滑系数来调整。

公式

假设 𝑦𝑡是在时间点 𝑡的实际观测值，我们定义两个状态变量：

𝑙𝑡 代表时间点 𝑡的水平分量。
𝑏𝑡 代表时间点 𝑡的趋势分量。

对于给定的平滑系数 𝛼 和 𝛽，其中 0<𝛼,𝛽<1，二指数平滑的更新规则如下：

水平分量的更新公式：
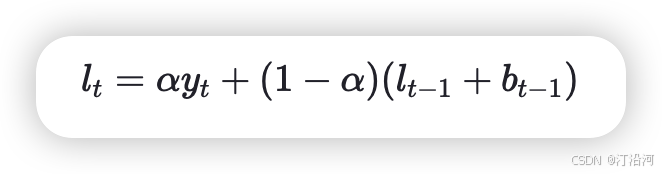
趋势分量的更新公式：

预测值可以通过水平分量和趋势分量的组合得出：

其中：

ℎ 表示预测步长，即从时间点 𝑡到未来时间点 𝑡+ℎ。
𝑦^𝑡+ℎ∣𝑡 表示基于时间点 𝑡 的信息对未来时间点 𝑡+ℎ的预测值。

参数解释

𝛼平滑系数：决定了当前观测值对水平分量的影响程度。较大的 𝛼α 值使得模型更加敏感于近期的变化。
𝛽平滑系数：决定了当前水平分量的变化对趋势分量的影响程度。较大的 𝛽β 值使得模型对趋势变化更敏感。

应用步骤

初始化：选择初始值 𝑙0 和 𝑏0。这通常可以通过观察序列的前几个值来估算。
更新水平分量和趋势分量：根据上述公式更新 𝑙𝑡 和 𝑏𝑡。
预测：使用水平分量和趋势分量的组合进行未来值的预测。

让我们计算前几个周期的水平项 𝑙𝑡lt 和趋势项 𝑏𝑡bt：

对于第一个周期 𝑡=1t=1：
𝑙1=𝛼⋅𝑦1+(1−𝛼)⋅𝑙0=0.2⋅50+(1−0.2)⋅50=50l1=α⋅y1+(1−α)⋅l0=0.2⋅50+(1−0.2)⋅50=50
𝑏1=𝛽⋅(𝑙1−𝑙0)+(1−𝛽)⋅𝑏0=0.1⋅(50−50)+(1−0.1)⋅5=5b1=β⋅(l1−l0)+(1−β)⋅b0=0.1⋅(50−50)+(1−0.1)⋅5=5
对于第二个周期 𝑡=2t=2：
𝑙2=𝛼⋅𝑦2+(1−𝛼)⋅(𝑙1+𝑏1)=0.2⋅55+(1−0.2)⋅(50+5)=54l2=α⋅y2+(1−α)⋅(l1+b1)=0.2⋅55+(1−0.2)⋅(50+5)=54
𝑏2=𝛽⋅(𝑙2−𝑙1)+(1−𝛽)⋅𝑏1=0.1⋅(54−50)+(1−0.1)⋅5=5.4b2=β⋅(l2−l1)+(1−β)⋅b1=0.1⋅(54−50)+(1−0.1)⋅5=5.4

第三个周期 (𝑡=3t=3):

𝑙3=𝛼⋅𝑦3+(1−𝛼)⋅(𝑙2+𝑏2)l3=α⋅y3+(1−α)⋅(l2+b2)

𝑙3=0.2⋅60+(1−0.2)⋅(54+5.4)l3=0.2⋅60+(1−0.2)⋅(54+5.4)

𝑙3=12+0.8⋅59.4l3=12+0.8⋅59.4

𝑙3=12+47.52l3=12+47.52

𝑙3=59.52l3=59.52

𝑏3=𝛽⋅(𝑙3−𝑙2)+(1−𝛽)⋅𝑏2b3=β⋅(l3−l2)+(1−β)⋅b2

𝑏3=0.1⋅(59.52−54)+(1−0.1)⋅5.4b3=0.1⋅(59.52−54)+(1−0.1)⋅5.4

𝑏3=0.1⋅5.52+0.9⋅5.4b3=0.1⋅5.52+0.9⋅5.4

𝑏3=0.552+4.86b3=0.552+4.86

𝑏3=5.412b3=5.412

第12个周期的计算：

4 三指数平滑

三指数平滑（Triple Exponential Smoothing），也称为Holt-Winters方法，是一种广泛应用于时间序列分析和预测的方法。这种方法适用于具有趋势和季节性模式的时间序列数据。

4.1 三指数平滑的基本概念

三指数平滑方法包括三个组成部分：水平分量（Level）、趋势分量（Trend）和季节性分量（Seasonality）。每个分量都通过指数平滑的方式进行更新。

水平分量（Level）

水平分量 𝑙𝑡lt 表示时间序列在给定时间点的平滑值。它是预测的基础。

趋势分量（Trend）

趋势分量 𝑏𝑡bt 描述了时间序列中的趋势变化率。

季节性分量（Seasonality）

季节性分量 𝑠𝑡st 捕获了数据中的周期性模式，例如年度销售周期等。

三指数平滑的公式

三指数平滑的更新公式通常如下：

其中，

𝑦𝑡是实际观测值。
𝑙𝑡 是水平分量。
𝑏𝑡 是趋势分量。
𝑠𝑡 是季节性分量。
𝑘 是季节长度（例如，如果数据按月度收集且每年有一个完整的周期，则 𝑘=12）。
𝛼、𝛽 和 𝛾 分别是水平、趋势和季节性分量的平滑参数，取值范围为 [0, 1]。

预测公式

使用场景

三指数平滑方法适用于以下场景：

时间序列数据具有明显的趋势和/或季节性。
需要预测未来一段时间内的数据。
数据集足够大以识别出趋势和季节性模式。
对于短期预测非常有效，但对于长期预测可能不太准确。

假设我们有10个观测值，并且我们想要预测第15个值。这意味着我们需要计算到第10个周期的所有分量，并使用这些分量来预测第11到第15个周期的值。

首先，我们需要知道是否有季节性。如果没有季节性，我们将使用双指数平滑（不考虑季节性分量）。如果有季节性，我们需要知道季节的长度 𝑘。

如果当前值不存在，使用预测值进行填充；

1 如果没有季节性

2 如果有季节性

4.2 ARIMA模型与三指数平滑的区别

ARIMA模型的特点

适用范围: 适用于非平稳时间序列。
参数: 包括自回归阶数(p)、差分阶数(d)、移动平均阶数(q)。
灵活性: 可以捕捉复杂的动态关系。
建模过程: 需要确定p、d、q的值，通常通过自相关函数（ACF）和偏自相关函数（PACF）图来辅助确定。
季节性: 可以扩展为季节性ARIMA（SARIMA）模型来处理季节性数据。

三指数平滑的特点：三指数平滑是一种专门针对具有趋势和季节性的时间序列数据的预测方法。

适用范围: 适用于具有趋势和/或季节性的平稳时间序列。
参数: 包括水平平滑因子（α）、趋势平滑因子（β）和季节性平滑因子（γ）。
简单性: 相对于ARIMA模型来说更加直观和易于实现。
建模过程: 不需要显式的差分步骤，通过平滑因子来调整模型的敏感度。
季节性: 可以处理季节性数据。

模型复杂度:
ARIMA模型可以捕捉更复杂的动态关系，而三指数平滑更侧重于趋势和季节性的平滑处理。
适用范围:
ARIMA模型适用于非平稳时间序列，而三指数平滑适用于具有趋势和/或季节性的平稳时间序列。
参数数量:
ARIMA模型通常有更多的参数（p、d、q），而三指数平滑则主要依赖于平滑因子（α、β、γ）。
模型选择:
在选择ARIMA模型时，需要确定p、d、q的值，而在三指数平滑中，主要是选择合适的平滑因子。
计算复杂度:
ARIMA模型通常需要更多的计算资源，特别是当参数较多时。
解释性:
三指数平滑模型更容易理解和解释，因为它直接反映了数据的趋势和季节性特征。

4.2.1 选择建议

如果数据具有明显的趋势和季节性，并且是平稳的，可以考虑使用三指数平滑。
如果数据是非平稳的，或者需要建模更复杂的动态关系，可以考虑使用ARIMA模型。
如果数据同时具有趋势、季节性和非平稳性，可以考虑使用季节性ARIMA模型。