Model-Based Reinforcement Learning via Meta-Policy Optimization

文献目录

先前的Model-based RL都想尽办法建立精确的动力学模型，试图通过描述模型的不确定性或学习一个robust的策略来解决模型偏差问题，但这是不够的，无法达到无模型方法的渐进性能。本文方法放弃了对这种精确性的依赖，通过学习一组动力学模型并将策略优化步骤作为元学习问题来实现，该策略可以通过一个梯度步骤快速适应任何拟合的动力学模型。本文方法包含两层循环，内部循环用于产生各个模型的适应策略，外部循环用于产生适应所有模型的元策略。

---

1. INTRODUCTION

背景：

• Model-free方法能够实现最优性能且易于实现，但其是以数据密集型为代价的，其高样本复杂性是应用于实际任务的主要障碍；
• Model-based方法通过使用环境动力学模型能够以显著较少的样本进行学习，然而，准确的动态模型往往比好的策略更复杂，只能在有限的问题集上学习好的策略，即使学习到了好的策略，它们的性能通常也会比无模型方法差很多。

基于模型的方法往往依赖于准确的（学习的）动力学模型来解决任务。 如果动力学模型不够精确，则策略优化很容易在模型的缺陷上过度拟合，从而导致行为不佳甚至导致灾难性故障。 这个问题在文献（PILCO: A Model-Based and Data-Efficient Approach to Policy Search）中被称为模型偏差。以前的工作试图通过描述模型的不确定性和学习一个健壮的策略来减轻模型偏差，通常使用集合来表示后验。 本文也使用了集合，但有很大不同。

我们提出了基于模型的元策略优化（MB-MPO），这是对先前基于模型的RL方法的一种正交方法：传统的基于模型的RL方法依赖于所学习的动力学模型来获得足够的精确性，从而能够学习在现实世界中同样成功的策略，但我们放弃了对这种精确性的依赖。我们可以通过学习一组动力学模型并将策略优化步骤作为元学习问题来实现。元学习，在RL的背景下，旨在学习一种快速适应新任务或环境的策略。通过将模型用作学习的仿真器，MB-MPO可以学习一种策略，该策略可以通过一个梯度步骤快速适应任何拟合的动力学模型。该优化目标将元策略引导到内部化动态预测的整体中一致的部分，同时将关于模型之间差异的最佳行为负担转移到适应步骤。这样，学习到的策略就显示出更少的模型偏差，而无需保守行事。虽然在如何收集轨迹样本和训练动态模型方面与以前的MB方法有很多相同之处，但是使用（和依赖）学习的动态模型进行策略优化是根本不同的。

在本文中，我们表明：

• 基于模型的策略优化可以学习与无模型方法的渐近性能相匹配的策略，同时显著提高样本效率；
• MB-MPO在挑战性控制任务上始终优于以前的基于模型的方法；
• 当模型有强烈偏差时，学习仍然是可能的。

我们方法的低样本复杂度使其可应用于现实世界的机器人技术。 例如，我们能够在两个小时的真实世界数据中学习高维和复杂的四足运动的最佳策略。 请注意，使用无模型方法学习这种策略所需的数据量要高10至100倍，并且，据作者所知，以前没有基于模型的方法能够在这样的任务中获得无模型性能。

2. Related Work

2.1 Model-Based Reinforcement Learning: Addressing Model Inaccuracies

使用简单的线性模型即可获得基于模型的RL的令人印象深刻的结果。 但是，像贝叶斯模型一样，它们的应用仅限于低维域。 我们使用神经网络（NN）的方法很容易扩展到复杂的高维控制问题。 用于模型学习的神经网络具有潜在的规模，可以解决样本复杂度高的高维问题。 使用大容量动态模型时的主要挑战是防止策略利用模型的不准确性。 一些工作通过学习模型的分布或通过学习自适应模型来解决模型偏差问题。 我们结合了通过学习模型集成来减少模型偏差的想法。 但是，我们证明了这些技术在具有挑战性的领域中并不足够，并且证明了元学习对于改善渐近性能的必要性。

过去的工作还试图通过策略优化过程来克服模型的不准确性。模型预测控制（MPC）通过在每个步骤进行重新规划来补偿模型的不完善之处，但其信用分配有限且计算成本较高。 鲁棒的策略优化寻找一种在各个模型之间都能很好执行的策略。 结果，策略往往过于保守。 相比之下，我们表明MB-MPO在模型一致的区域中学习了一种可靠的策略，而在模型得出的预测相差很大的地方则采用了一种自适应策略。

2.2 Model-Based + Model-Free Reinforcement Learning

自然地，希望将基于模型的方法和没有模型的方法结合起来，以实现高性能和低样本复杂性。将它们结合的尝试可以大致分为三种：

• 首先，微分轨迹优化方法通过学习到的动力学模型传播策略或价值函数的梯度。然而，这些模型并没有被明确地训练成近似一阶导数，并且在反向传播时，它们遭受梯度爆炸和梯度消失的困扰；
• 其次，模型辅助的MF方法使用动态模型通过想象策略推出（rollouts）来增加真实环境数据。这些方法仍然在很大程度上依赖于现实世界的数据，这使得它们对于真实世界的应用是不切实际的。借助元学习，如果需要，我们的方法可以以更少的样本快速适应现实世界；
• 第三，最近的工作通过完全使用学习模型中的样本将MF模块与实际环境完全分离。即使考虑模型不确定性，这些方法仍然依靠动态模型的精确估计来学习策略。相比之下，我们对模型集成进行元学习，通过在预测不确定性较高时通过训练适应性来减轻对精确模型的强烈依赖。 ME-TRPO可以看作是在不执行任何自适应的情况下算法的边缘情况。

2.3 Meta-Learning

我们的方法利用元学习来解决模型的不准确性。 元学习算法旨在学习可以适应新场景或具有少量数据点的任务的模型。当前的元学习算法可以分为三类。

• 一种方法涉及训练循环或记忆增强网络，该网络吸收训练数据集并输出学习者模型的参数；
• 另一组方法将数据集和测试数据馈入一个循环模型中，该模型输出测试输入的预测；
• 最后一类将优化问题的结构嵌入到元学习算法中。

这些算法已扩展到RL的上下文（context）。 我们的工作基于MAML。然而，在以往的元学习方法中，每个任务通常由不同的奖励函数定义，而我们的每个任务则由不同学习模型的动力学定义。

3. Background

3.1 Model-based Reinforcement Learning

离散时间有限马尔科夫决策过程$M\sim (S,A,p,r,\gamma ,p_0,H)$

• $S$为状态集合；
• $A$为行为空间；
• $p(s_{t+1}|s_t,a_t)$为转换分布；
• $r:S\times A\to \mathbb{R}$为奖励函数；
• $p_0:S\to {\mathbb{R}}_{+}$为初始状态分布；
• $\gamma$为折扣因子；
• $H$是过程的视野（长度）；
• 轨迹$\tau =(s_0,a_0,...,s_{H-1},a_{H-1},s_H)$；

定义MB方法中的动力学模型为${\hat{p}}_{\varphi }(s^{\prime }|s,a)$，在这种情况下，动态模型的参数$\varphi$被优化以最大化状态转移分布的对数似然。

3.2 Meta-Learning for Reinforcement Learning

Meta-RL旨在学习一种学习算法，该算法能够根据一组MDP上的分布$\rho (M)$快速学习MDPs $M_k$中的最佳策略。MDPs $M_k$的奖励函数$r_k(s,a)$和转换分布$p_k(s_{t+1}|s_t,a_t)$可能不同，但共享动作空间$A$和状态空间$S$。

我们的方法建立在基于梯度的元学习框架MAML的基础上，该框架在RL环境下训练参数策略${\pi }_{\theta }(a|s)$，以通过一个或几个常规策略梯度步骤快速改进其在新任务中的性能。 MAML的元训练目标可以写为：

MAML尝试学习初始化${\theta }^{\ast }$，以便对于任何任务$M_k\sim \rho (M)$，在一个策略梯度步骤之后，该策略在相应任务中均能达到最佳性能。

4. Model-Based Meta-Policy-Optimization

要实现复杂的高维实际机器人技术任务，需要将当前基于模型的方法扩展到无模型的能力，同时还要保持其数据效率。我们的方法是基于模型的元策略优化（MB-MPO），它通过将基于模型的RL框架化为目标，从而实现了关于动态模型分配的元学习策略，主张最大限度地提高策略适应性，而不是鲁棒性， 当模型不一致时。 这不仅消除了为在不同动态模型之间表现良好的单个策略进行优化的艰巨任务，而且还带来了更好的探索性能和所收集样本的更高多样性，从而改善了动态估计。

我们通过使用一组学习到的动态模型并通过元学习策略来实例化此通用框架，该策略可以通过一个策略梯度步骤快速适应任何动态模型。 在下文中，我们首先描述如何学习模型，然后解释如何在一组模型上对策略进行元训练，最后，我们提出整体算法。

4.1 Model Learning

该方法的一个关键组成部分是以集成的形式学习真实环境动力学模型的分布。为了消除模型的相关性，每个模型的随机初始化是不同的，并用采集到的真实环境样本的不同随机选择子集$D_k$对其进行训练。为了解决在整个元优化过程中，随着策略的变化而发生的分布变化，我们经常在当前策略下采集样本，与之前的数据$D$进行聚合，并用热启动重新训练动态模型。

在我们的实验中，我们认为动态模型是当前状态$s_t$和行动$a_t$的一个确定性函数，采用前馈神经网络来近似它们。我们遵循基于模型的RL的标准实践，即训练神经网络来预测状态$\Delta s=s_{t+1}-s_t$（而不是下一个状态$s_{t+1}$）的变化。我们用${\hat{f}}_{\varphi }$表示下一状态的函数逼近器，它是输入状态和神经网络输出的和。学习集合的每个模型${\hat{f}}_{{\varphi }_k}$的目的是找到最小化$l_2$一步预测损失的参数向量${\varphi }_k$：

其中$D_k$是存储agent经历的转换的训练数据集$D$的采样子集。遵循避免过度拟合和促进快速学习的标准技术，具体来说：

• 基于验证损失提前停止训练;
• 规范化神经网络的输入和输出;
• 权重规范化。

4.2 Meta-Reinforcement Learning on Learned Models

给定特定环境中学习到的动态模型的集合，我们的核心思想是学习一种可以快速适应任何这些模型的策略。 要学习此策略，我们将基于梯度的元学习与MAML结合使用（在第3.2节中进行介绍）。 为了在元学习的上下文中正确地表达这个问题，我们首先需要定义一个适当的任务分布。

考虑到近似真实环境动态性的模型 { f ^ ϕ 1 , f ^ ϕ 2 , . . . , f ^ ϕ K } \{\hat{f}_{\phi_1},\hat{f}_{\phi_2},...,\hat{f}_{\phi_K}\} {f^​ϕ1​​,f^​ϕ2​​,...,f^​ϕK​​}，我们可以使用这些学习的动态性模型将它们嵌入不同的MDPs $M_k=(S,A,{\hat{f}}_{{\varphi }_k},r,\gamma ,p_0)$中，从而构建统一的任务分布。 我们注意到，不同于先前的实验方法，在我们的工作中，奖励函数在任务之间保持不变，而动态变化。 因此，每一个任务都构成了一个关于真实环境中动态的不同信念。 最后，我们将目标定位为以下元优化问题：

其中$J_k(\theta )$是策略${\pi }_{\theta }$下由模型${\hat{f}}_{{\varphi }_k}$评估的期望奖励。

为了估计公式4中的期望并计算相应的梯度，我们从假想的MDPs中取样轨迹。奖励是在给定预测的状态和动作后通过评估奖励函数$r({\hat{f}}_{{\varphi }_k}(s_{t-1},a_{t-1},a_t))$来计算的，我们假设它是给定的。特别地，当估算适应目标$J_k(\theta )$时，元策略${\pi }_{\theta }$被用来对每个模型${\hat{f}}_{{\varphi }_k}$抽样一组虚拟路径$T_k$。对于元目标$\frac{1}{K}{\sum }_{k=0}^K{J}_k({\theta }_k^{\prime })$，我们使用模型${\hat{f}}_{{\varphi }_k}$和通过将参数$\theta$调整到$k$-th模型获得的策略${\pi }_{{\theta }_k^{\prime }}$生成轨迹rollouts $T_k^{\prime }$。因此，没有真实的数据用于元策略优化的数据密集步骤。

实际上，可以选择任何策略梯度算法来执行策略参数的元更新。 在我们的实现中，我们使用TPRO来最大化元目标，并使用VPG进行适应步骤。为了减少策略梯度估计的方差，使用了线性奖励基线。

4.3 Algorithm

在下文中，我们描述了该方法的整体算法（请参阅算法1）。 首先，我们使用不同的随机权重初始化模型和策略。 然后，我们进入数据收集步骤。 在第一次迭代中，使用统一的随机控制器从现实世界中收集数据，并将其存储在缓冲区$D$中。在随后的迭代中，使用调整后的策略{${\pi }_{{\theta }_1^{\prime }},...,{\pi }_{{\theta }_K^{\prime }}$}收集来自现实世界的轨迹，然后将其与之前迭代的轨迹聚合。按照第4.1节中说明的步骤，使用聚合的真实环境样本训练模型。 该算法通过使用策略${\pi }_{\theta }$从模型 { f ϕ 1 , . . . , f ϕ K } \{f_{\phi_1},...,f_{\phi_K}\} {fϕ1​​,...,fϕK​​}的每个集合中想象轨迹来进行。这些轨迹被用来执行内部适应策略梯度步骤，从而产生适应策略 { π θ 1 ′ , . . . , π θ K ′ } \{\pi_{\theta_1'},...,\pi_{\theta_K'}\} {πθ1′​​,...,πθK′​​}。最后，我们使用调整后的策略${\pi }_{{\theta }_k^{\prime }}$和模型$f_{{\varphi }_k}$生成虚拟轨迹，并针对元目标优化策略（如第4.2节所述）。我们反复执行这些步骤，直到达到所需的性能。该算法返回最优的预更新参数${\theta }^{\ast }$。

5. Benefits of the Algorithm

与传统的基于模型和无模型的方法相比，使用虚构的轨迹rollouts来对一组动态模型进行元学习策略提供了许多好处。下面我们将讨论这些优点，旨在为算法提供直观性。

5.1 Regularization effect during training

优化策略以在一个策略梯度步骤内适应任何拟合模型都会对策略学习产生正则化效果（如在监督学习案例中观察到的[43]）。 元优化问题将策略引导到具有较高动态模型不确定性的区域，以提高可塑性，从而将适应模型差异的负担转移到内部策略梯度更新上。

我们将可塑性视为策略在参数空间中进行小幅度更改（即梯度更新）以更改其（有条件的）分布的能力。 策略可塑性通过更新前后策略之间的统计距离来体现。 在第6.3节中，我们分析了模型不确定性与策略可塑性之间的联系，发现模型集合的预测方差与${\pi }_{\theta }$和${\pi }_{{\theta }_k^{\prime }}$之间的KL散度之间存在很强的正相关。 这种效果会阻止策略学习在robust策略优化中出现的次优行为。 更重要的是，一旦动力学模型变得更加准确，则这种正则化效果就会消失，如果为学习的模型提供了足够的数据，则会导致渐近最优策略。 在6.4节中，我们展示了此属性如何使我们能够从嘈杂且高度偏差的模型中学习。

5.2 Tailored data collection for fast model improvement

由于我们使用通过适应每个模型而获得的不同策略{${\pi }_{{\theta }_1^{\prime }},...,{\pi }_{{\theta }_K^{\prime }}$}对真实环境轨迹进行采样，因此收集的训练数据更加多样化，从而提高了动态模型的鲁棒性。 具体而言，调整后的策略倾向于利用各个动态模型的特征缺陷。因此，我们在动态模型不能充分接近真实动态的区域收集真实数据。这种效果加速了模型不精确性的修正，从而加快了改进的速度。在附录A.1中，我们通过实验证明了定制数据收集对性能的积极影响。

5.3 Fast fine-tuning

元学习优化了一种策略，可以快速适应一系列任务。在我们的例子中，每个任务对应于对真实环境动态可能的不同believe。当未达到最优性能时，模型的集合将在其预测中呈现高度差异，增加了真实动态依赖于置信分布支持的可能性。因此，学习到的策略很可能表现出对真实环境的高度适应性，并且与从头开始或从任何其他MB初始化训练策略相比，在实际环境中使用VPG对策略进行微调可以导致更快的收敛速度。

5.4 Simplicity

与以前的方法相反，我们的方法很简单：它不依赖于参数噪声探索，模型权重或策略熵的仔细重新初始化，难以训练概率模型，并且不需要解决模型分布不匹配的问题。

6. Experiments

我们的实验评估的目的是研究以下问题：

• 在样本复杂度和渐近性能方面，MB-MPO与最新的无模型方法和基于模型的方法相比如何？
• 模型不确定性如何影响策略的可塑性？
• 我们针对不完善模型的方法有多健壮（robust）？

为了回答提出的问题，我们在Mujoco仿真器中评估了六个连续控制基准任务的方法。 附录A.3中提供了环境描述以及实验设置的详细说明。 在接下来的所有实验中，我们使用预更新策略来报告使用我们的方法获得的平均回报。报告的性能是至少三个随机种子的平均值。

6.1 Comparison to State-of-the-Art: Model-Free

我们将我们的方法在样本复杂度和性能上与四种最先进的无模型RL算法进行比较：深度确定性策略梯度（DDPG）、信赖域策略优化、近端策略优化（PPO）和使用Kronecker-Factored信赖域（ACKTR）的行为批评者。结果如图1所示。

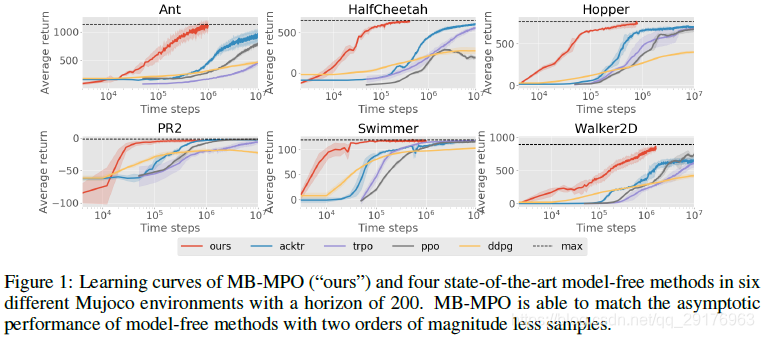
在所有运动任务中，与无模型方法相比，我们使用的数据量少10到100倍，从而可以实现最高性能。 在最具挑战性的领域：ant，hopper和walker2D； 我们方法的数据复杂度比MF小两个数量级。 在更简单的任务中：模拟的PR2和swimmer，我们的方法使用少20到50倍的数据实现了MF的相同性能。 这些结果凸显了MB-MPO在实际机器人任务中的优势。 对于较简单的域，要获得最大回报所需的实际数据量相当于30分钟，对于较复杂的域，则相当于90分钟。

6.2 Comparison to State-of-the-Art: Model-Based

我们还将我们的方法与最近基于模型的工作进行了比较：模型集成信任区域策略优化（ME-TRPO），以及Nagabandi等人介绍的基于模型的方法，它使用MPC进行规划（MB-MPC）。

结果如图2所示，突出了MB-MPO在复杂任务中的优势。 MB-MPC难以在需要robust规划的任务上很好地执行，而在需要中/长期计划的任务（如hopper）中完全失败。相反，ME-TRPO能够学习更好的策略，但是与MB-MPO相比，此类策略的收敛速度较慢。此外，尽管ME-TRPO在复杂域中收敛到次优策略，但MB-MPO能够实现最高性能。

6.3 Model Uncertainty and Policy Plasticity

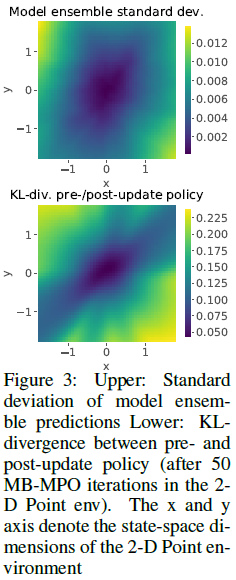
在第6.3节中，我们假设，在具有高动态模型不确定性的区域，元优化将策略转向更高的可塑性，同时将一致的模型预测嵌入到预更新策略中。为了对这个假设进行实证分析，我们在一个简单的二维点环境中进行了一个实验，在这个环境中，从$[-2,2{]}^2$开始的代理必须到达目标位置$(0,0)$。我们使用${\pi }_{\theta }$和不同适应策略${\pi }_{{\theta }_k^{\prime }}$之间的平均KL散度来测量$s$状态下的可塑性。

图3描述了更新前和更新后策略之间的KL散度，以及在状态空间上整体预测的标准偏差。 由于代理倾向于环境中心，因此该区域中有更多过渡数据可用。因此，模型在中心具有更高的精度。 结果表明，模型不确定性与更新前和更新后策略之间的KL差异之间存在很强的正相关性。 我们发现，在整个培训过程中以及不同的超参数配置之间，策略可塑性和预测不确定性之间始终存在这种联系。

6.4 Robustness to Imperfect Dynamic Models and Compounding Errors

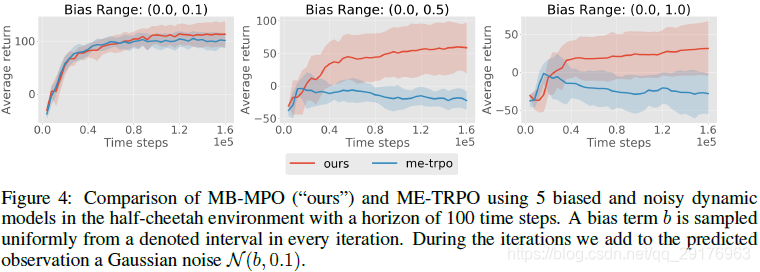
我们提出的问题是，对于不完美的动力学预测，我们提出的算法的鲁棒性如何。我们从两个方面来研究它。首先，以一个明显错误的动力学模型为例。具体地说，我们将有偏高斯噪声$N(b,0.1^2)$添加到下一个状态预测中，从而在每个模型的每次迭代中对有偏高斯噪声$b$重新采样。第二，我们提出了一个需要长期预测的现实案例。长期自举模型预测会导致很高的复合误差，使得对此类预测的策略学习具有挑战性。

图4描述了我们的方法和ME-TRPO在half-cheetah环境中对不同$b_{max}$值的性能比较。结果表明，当暴露于有偏和噪声的动力学模型时，我们的方法始终优于ME-TRPO。ME-TRPO在强偏差（即$b_{max}=0.5$和$b_{max}=1.0$）的情况下无法学习策略，但我们的方法，尽管动态预测严重受损，仍然能够学习正向速度下的运动行为。

此属性还体现在长期任务中。图5比较了我们的方法与内部学习率$\alpha =10^{-3}$相对于边缘情况$\alpha =0$（不进行适应）的性能。 对于每个随机种子，MB-MPO都会稳定收敛以达到最佳性能。但是，如果没有适应，学习就会变得不稳定，并且不同的种子会表现出不同的行为：适当的学习，陷入次优的行为，甚至是不学习良好的行为。

7. Conclusion

在本文中，我们提出了一种简单且普遍适用的算法，即基于模型的元策略优化（MB-MPO），该算法学习了动力学模型的集合并针对每个学习的模型对策略进行了元优化。我们的实验结果表明，在一组完整的学习模型上进行元学习策略，可以提供与最新的无模型方法相同的性能水平，并且样本复杂度大大降低。我们还将我们的方法与以前的基于模型的方法进行比较，以获得更好的性能和更快的收敛性。我们的分析证明了现有方法无法克服模型偏差，并展示了我们针对不完善模型的方法的鲁棒性。因此，我们能够将基于模型的扩展到更复杂的域和更长的视野。值得进一步研究的一个方向是使用贝叶斯神经网络而不是集成来学习动力学模型的分布。最后，未来工作的一个令人兴奋的方向是将MB-MPO应用于实际系统。