现代计算机图形学Games101入门笔记(五)

反走样和深度缓冲

强关联 采样

采样问题

锯齿

摩尔纹

车轮效应

前两个是空间，第三个时间

本质上信号变化太快，采样跟不上速度。

反走样 模糊

先模糊，再采样,反走样。要是先采样，再模糊呢？不行。

频域

f=频率  T周期，根据f判断快慢，还能知道周期T重复一次

傅里叶级数展开

与傅里叶变换概念上相似。

给定一个函数，经过复杂变换，变成新函数，还能变回来，就是傅里叶变换和逆傅里叶变换。

再看，傅里叶级数展开。一个波，经过复杂变化，变成新的波，还能再变回去的过程。

频率越高，采样速度就需要越快，不然走样严重，恢复不出原来的样子。

这两个不同的信号，采样的结果是一样的，这就是走样。

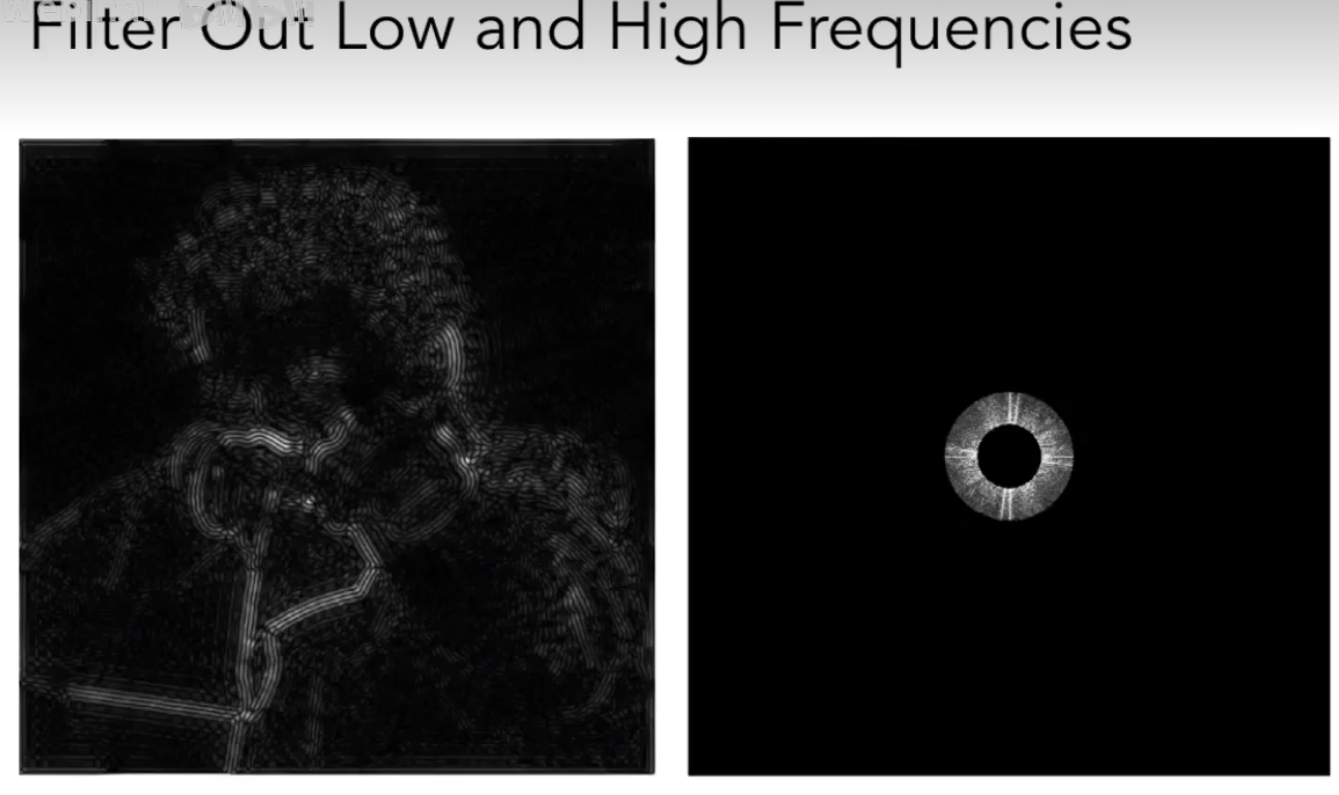
拿一张照片，观察一下它的频谱。发现十字线，就是边缘出现颜色变化较大，左右上下两边不是平和过渡导致的，白色低频，黑色高频。

高通滤波（边界）

低通滤波（模糊）

覆盖卷积（Convolution）

图形学上简化定义，它信号任意一个数取周围加权平均。对信号用某种滤波器使用卷积操作，得到新的信号，卷积操作。为了理解。

卷积定理

实域上的如果对两个信号进行卷积，那对应在频域上两个信号频域上的乘积。

通过定理如何做卷积。

拿到一张图片可以用某一个卷积的滤波器去做一个卷积操作，也可以把这个图先傅里叶变换到频域上，把卷积滤波器也变频域上，这两个直接相乘，得到频域结果，再逆傅里叶变换变到实域上，结果是一致的。实域上的如果对两个信号进行卷积，那对应在频域上两个信号频域上的乘积。

还有 实域的乘积也想当于频域的卷积。

用更大box，只能留下更低的滤波，结果变得更模糊

在频率上看什么是采样，采样就是在重复一个原始信号的频谱。

走样在频谱上，就是有重叠。频域和实域上的有很多相反关系，采样越稀疏，搬运频谱上越密集。

反走样

1.增加采样率。2.高清显示设备，提升分辨率。

对应先模糊再采样方式，拿掉高频信息。

MSAA用更多的采样点来反走样，只是近似，不能解决反走样问题。增大了计算量。4倍？可以使用样本再提升性能。

还有FXAA和TAA。

属于图像后处理过程，与增加样本数没关系，先把锯齿得出，然后做些什么样的操作，在把锯齿弄掉。FXAA，是无锯齿边界，比对，把多出来的锯齿移除。TAA,找上一帧的操作。

Super resolution  一张512*512 拉大到1024*1024，那细节缺失用DLSS方式处理深度学习来估算缺失图像技术。