无权图的最短路径

无权图的最短路径可以分为单源最短路径和多源最短路径。
无权图单源最短路径：从某个固定点出发，求其到所有其他定点的最短路径。
无权图多源最短路径：求任意两个结点之间的最短路径。

单源最短路径算法，其实就是通过按照递增（非递减）的顺序找到各个定点的最短路；换个角度思考，就是通过BFS（广度优先搜索），算出每一层的最短路径。例如，先计算V结点的邻接点的最短路径，之后再计算V结点每一个邻接点W1，W2，W3 等的每一个邻接点进行遍历，更新最短距离。

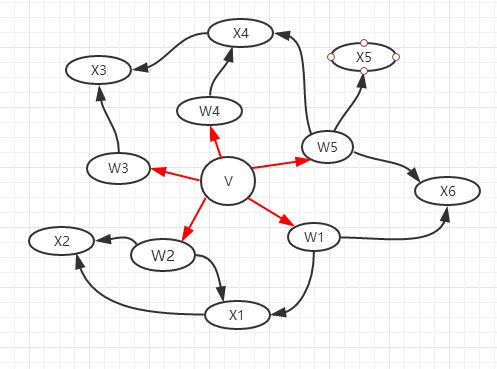
如下图所示：

先将根结点V压入堆栈，之后，出栈，对每一个V的邻接点，计算dist[]，并记录path[]，之后将其入栈。进行下一轮。注意：最短路径算法的核心在更新路径。无权图的路径相当于每次BFS后，外圈路径+1。

伪码描述：

void Unweighted(Vertex S)
{
    Enqueue(S,Q);
    while(!IsEmpty(Q)){
        V = Dequeue(Q);
        for(each W in V)
            if(dist[W]==-1){
                dist[W] = dist[V] + 1;
                Path[W] = V;
                Enqueue(W,Q);
            }
    }
}

这里值得注意的是，无权图的单源最短路初始化的时候，如果根据dist的大小来判别图结点是否被访问过，则dist[] 不能全部初始化为0。
因为原点到自己的距离为0（这里不考虑负值圈），如果其他点的距离初始化再和原点相等，则会出现

void Unweighted(Vertex S)
{
    Enqueue(S,Q);
    while(!IsEmpty(Q)){
        V = Dequeue(Q);
        for(each W adjoin V)
            if(dist[W]==0){  /*初始化为0，并不能标记原点被访问过*/
                dist[W] = dist[V] + 1;
                Path[W] = V;
                Enqueue(W,Q);
            }
    }
}

运行时，第一步为从起点V到起点可达的W顶点，此时dist[W]=1;Path[W]=V;
第二步W会回到V并且dist[V]=2,Path[V]=W;
此时会继续运行
终于
到了打印Path的时候了
ERROR
你发现在这里出现了死循环（无法找到原点，类似无法找到数的根节点）
WVWVWVWVW….