用python模拟天体运动(二体运动与天体轨道稳定问题)

目录

1. 模拟天体运动的代码

2. 运行效果

3. 非平方反比(轨道稳定性问题)

---

1. 模拟天体运动的代码

接下来我们将用python模拟实现天体运动

以下是我们所需要的库：

import matplotlib.pyplot as plt  
import matplotlib.animation as animation  
import numpy as np  

我们定义常量：

G = 6.67430e-11               # 引力常数
p = 2                         # 引力定律
dt = 3600*24                  # 时间步长
Earth_mass = 5.972e24         # 地球质量
Sun_mass = 1.989e30           # 太阳质量
Earth_position = (1.496e11, 0)# 地球位置
Sun_position = (0, 0)         # 太阳位置

# 宇宙第一速度，宇宙第二速度
v_orbit = np.sqrt(G*Sun_mass/np.sqrt((Earth_position[0])**2 + ((Earth_position[1]))**2))
v_escape = np.sqrt(2)*v_orbit

# 地球速度
#Earth_velocity = (0, v_orbit)
#Earth_velocity = (0, v_escape)
Earth_velocity = (0, 29784.6)

为了方便计算，我们定义一个行星类

class Planet:  
    def __init__(self, name, mass, initial_position=(0, 0), initial_velocity=(0, 0)):  
        self.name = name  
        self.loc = np.array(initial_position)  # 使用NumPy数组来存储位置  
        self.v = np.array(initial_velocity)  # 使用NumPy数组来存储速度  
        self.a = np.array([0, 0])  # 加速度  
        self.force = np.array([0, 0])  # 作用力  
        self.m = mass  # 行星的质量  
        self.trail = []  # 存储轨迹点的列表  
  
    def update_location(self, dt, other_planet):  
        # 计算两行星之间的距离  
        r_val = np.linalg.norm(np.array(self.loc) - np.array(other_planet.loc))  
        # 计算引力  
        self.force = G * self.m * other_planet.m / r_val ** (p) * (other_planet.loc - self.loc) / r_val  
        # 更新加速度  
        self.a = self.force / self.m  
        # 更新速度  
        self.v += self.a * dt  
        # 更新位置  
        self.loc += self.v * dt  
        # 将当前位置添加到轨迹列表中  
        self.trail.append(self.loc.tolist()) 

行星类的实例化

# 初始化太阳和地球  
Sun = Planet("Sun", Sun_mass, Sun_position)  
Earth = Planet("Earth", Earth_mass, Earth_position, Earth_velocity)  
  
# 初始化模拟和图形  
fig, ax = plt.subplots()  
  
# 绘制太阳  
sun_scatter, = ax.plot(Sun.loc[0], Sun.loc[1], 'yo')  
  
# 初始化地球的位置  
earth_scatter, = ax.plot(Earth.loc[0], Earth.loc[1], 'bo')  
  
# 初始化地球的轨迹  
trail, = ax.plot([], [], 'b-')

模拟行星运动：

# 设置坐标轴限制  
ax.set_xlim(-3e11, 3e11)  
ax.set_ylim(-3e11, 3e11)  
ax.set_aspect('equal', adjustable='box')  
  
# 动画更新函数  
def update(frame):  
    # 更新地球的位置  
    Earth.update_location(dt, Sun)  
      
    # 更新地球的位置散点  
    earth_scatter.set_data(Earth.loc[0], Earth.loc[1])  
      
    # 更新地球的轨迹  
    trail.set_data([x[0] for x in Earth.trail], [x[1] for x in Earth.trail])  
      
    # 返回更新后的对象列表  
    return sun_scatter, earth_scatter, trail,  
  
# 创建动画  
ani = animation.FuncAnimation(fig, update, frames=np.arange(0, 365*24*3600, 3600),  
                               interval=1, blit=True)  
  
# 显示图形  
plt.show()

2. 运行效果

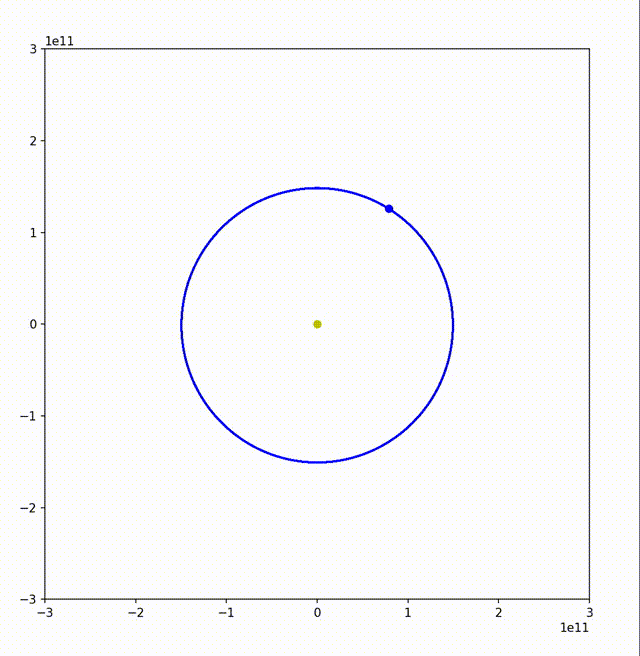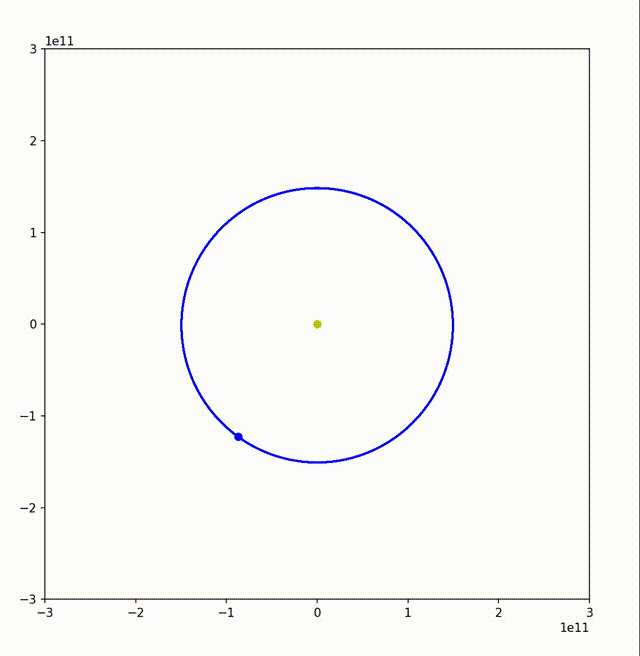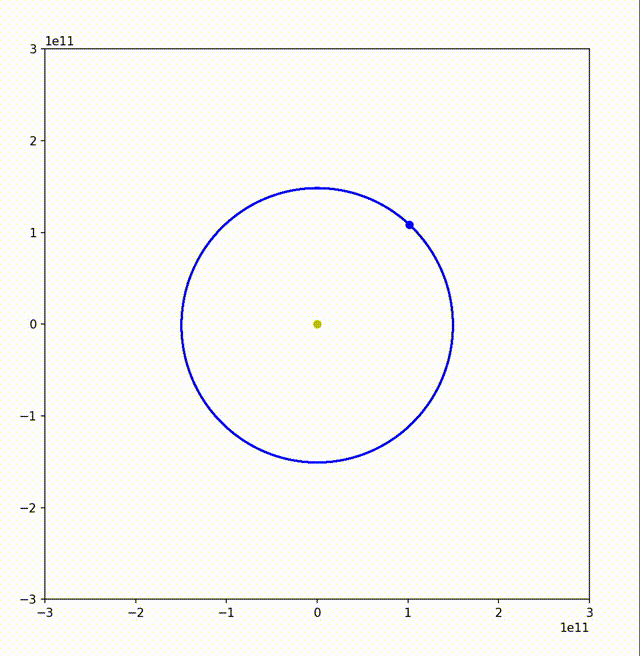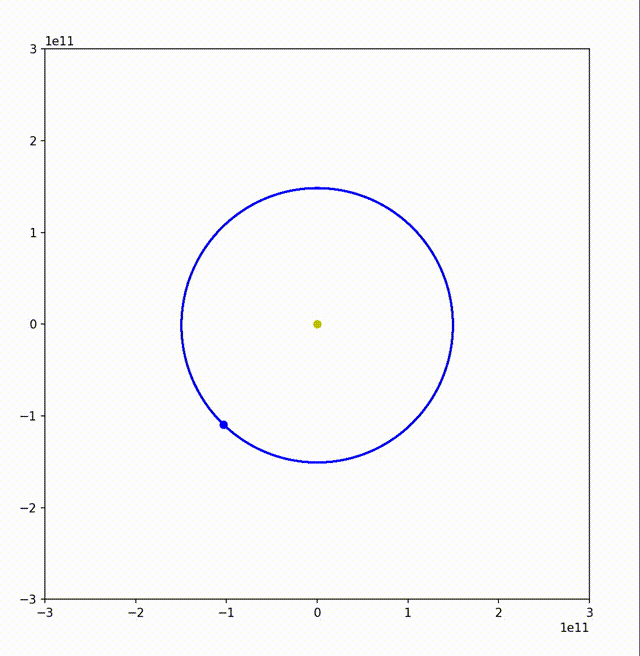
可以看到，地球的运行轨迹还是非常接近正圆的。

我们稍微改变一下参数，让地球的速度变慢些和变快血，得到：

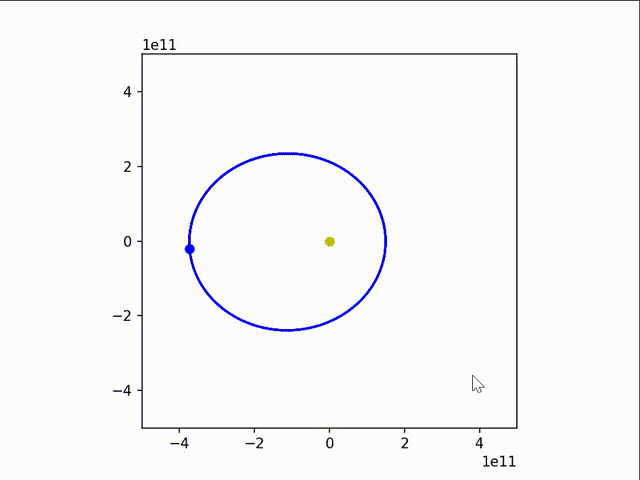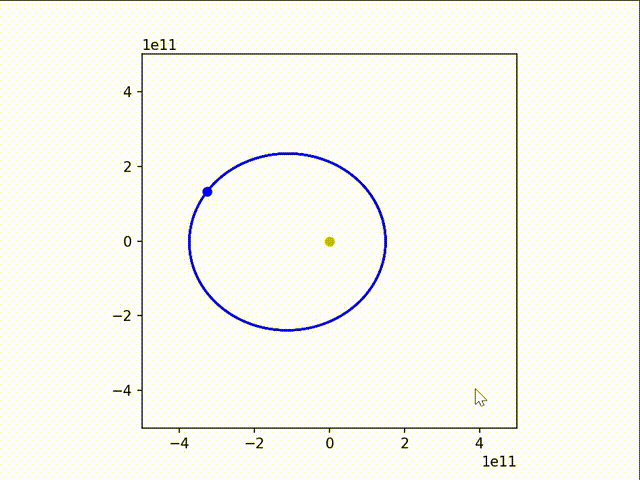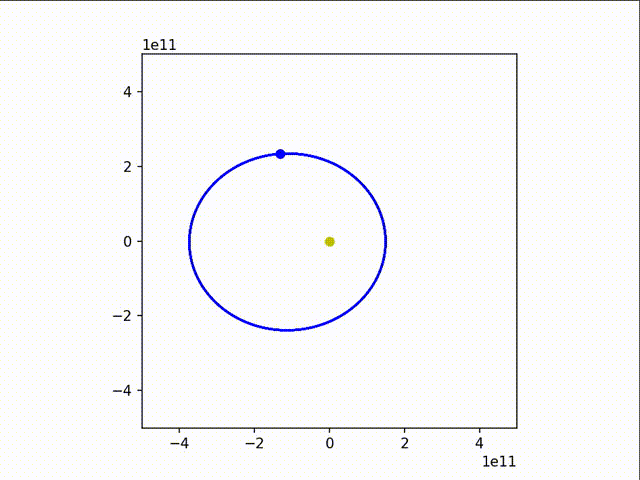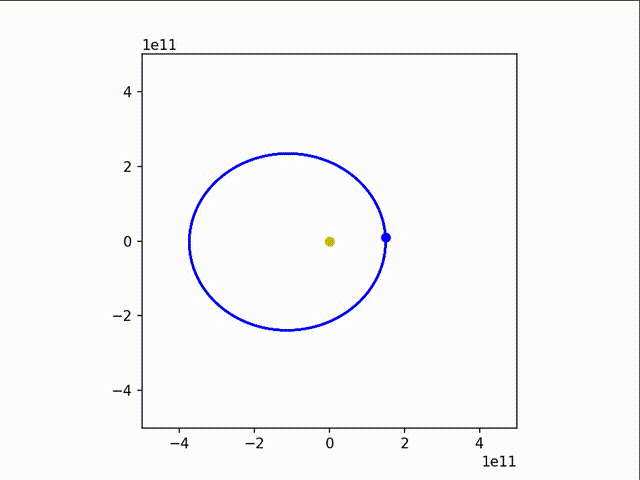
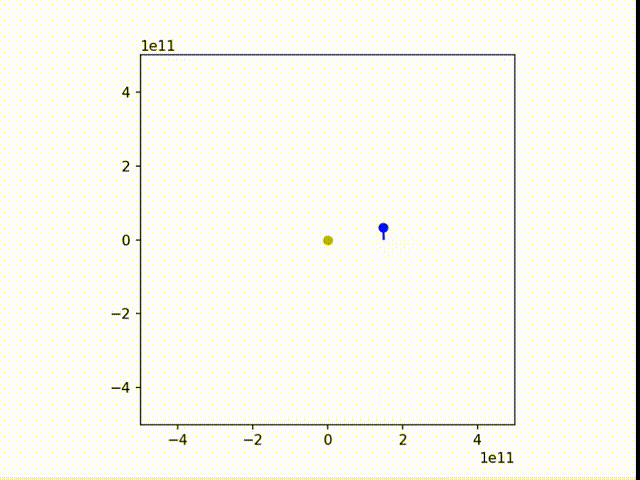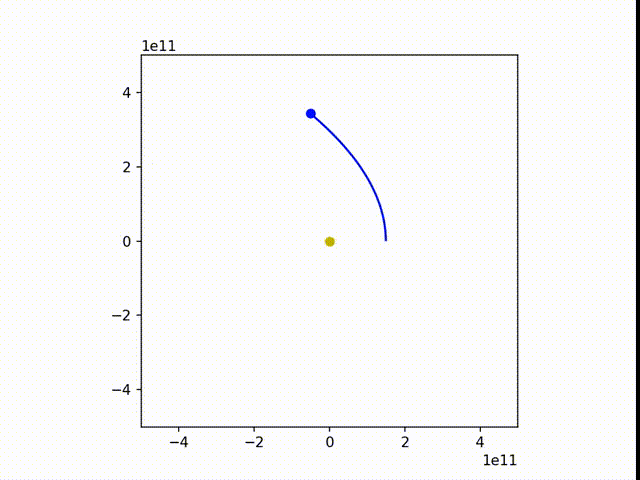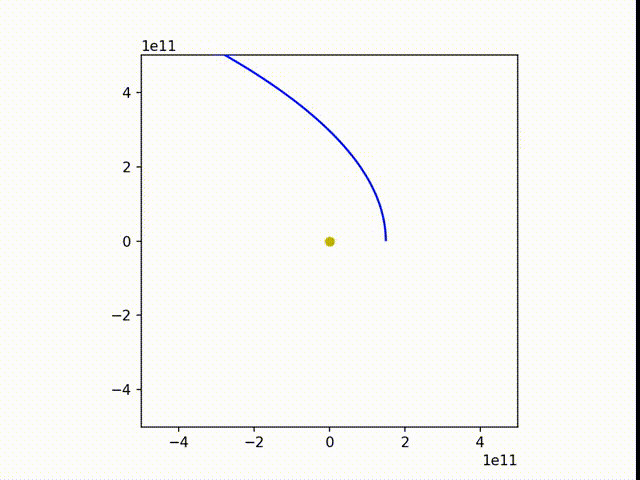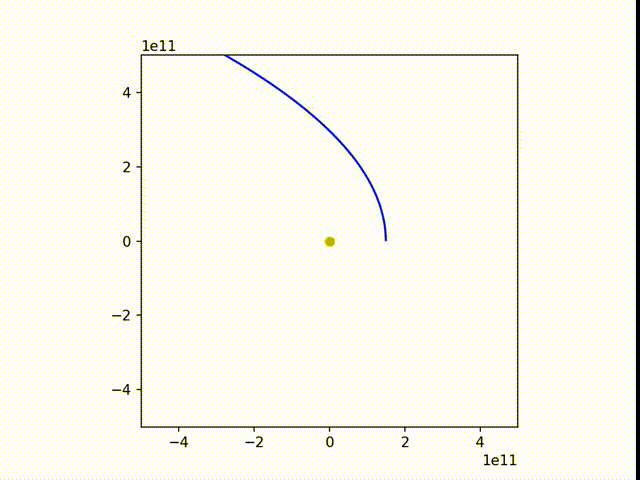
3. 非平方反比(轨道稳定性问题)

根据理论力学，我们知道，只有引力是符合平方反比定律或正比于距离的时候天体的轨道才有可能是稳定且闭合的。如果不是平方反比，而是2.1次方反比和1.9次方反比定律呢？

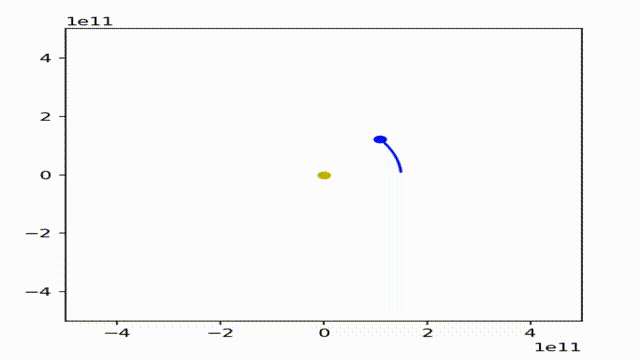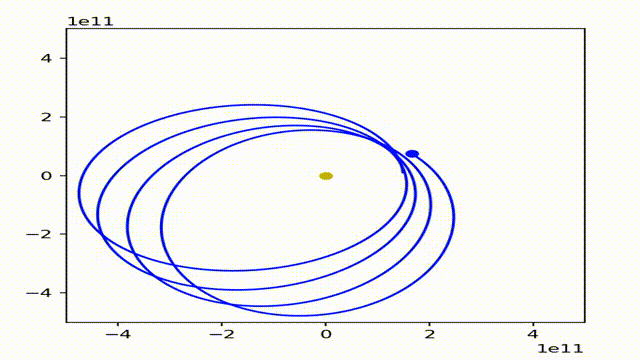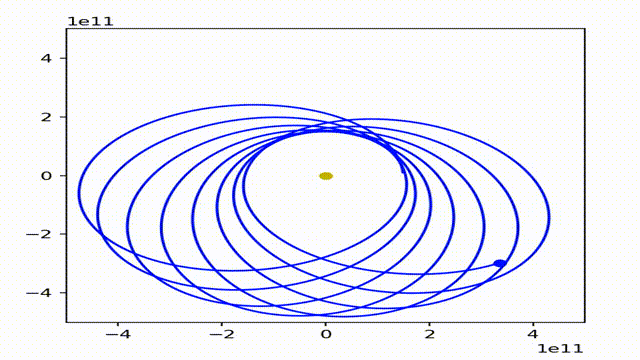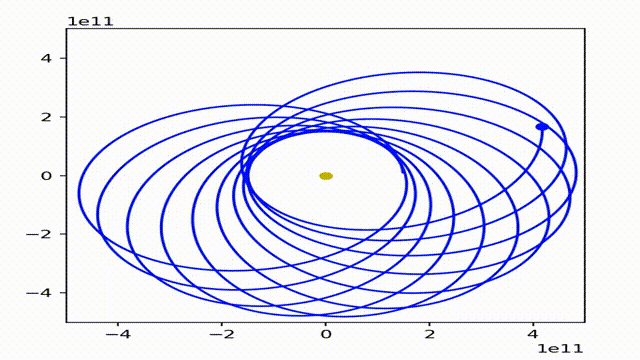
事实上，它们的图像都是这样的形势的。(不知道为什么图片变扁了)。有趣的是，行星始终在一个环形区域内运动。而这个轨道是稠密的，也就是说，只要时间足够，行星就能够与该环形区域内的任意一点无限接近。当且仅当 1<p<3时成立。其中 F = G M m / r^p