求圆外一点做圆切线的切点坐标（算法）

求圆外一点做圆切线的切点坐标（算法）

求圆外一点做圆切线的切点坐标（算法）

解此题的常规方法是圆的方程和切线方程联立解的两个点的坐标，这种方法过于繁琐，而且在代码中不易实现。由此想到用向量旋转来解此题，解法如下。

知识点提要

二维坐标下向量旋转后的向量坐标公式。如下图：

解题思路

解题思路就是通过以点到圆心的向量旋转得到新的点到圆心的向量，然后乘以模长得到坐标。

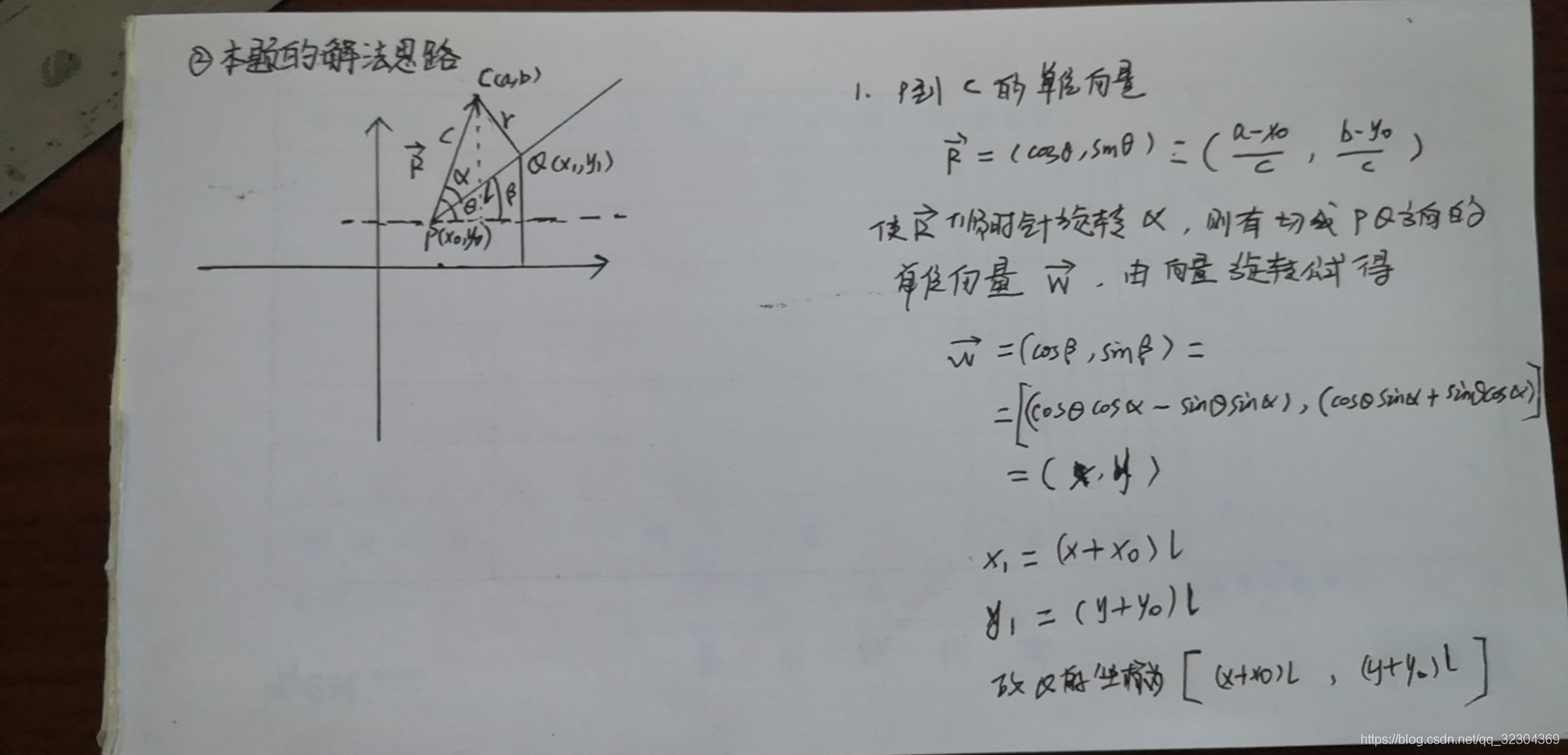
C程序代码

#include <stdio.h>
#include<math.h>
struct Point
{  // 声明结构体类型
    double x;      // 该点的x坐标
    double y;      // 该点的y坐标
}C,P,Q1,Q2,U;
// C是圆心的坐标 P是点的坐标 Q1,Q2是切点坐标 U是点到圆心的单位向量坐标
int main()
{
    double r =0; // 圆的半径
    double distance=0; // 圆心r 到p 点的距离
    double length=0; // 点p 到切点的距离
    double angle =0; // 切线与点心连线的夹角
    
    printf("请输入C点坐标：\n");
    scanf("%lf %lf",&C.x,&C.y);
    printf("请输入P点坐标:\n");
    scanf("%lf %lf",&P.x,&P.y);
    printf("请输入圆的半径:\n");
    scanf("%lf",&r);
    // 求出点到圆心的距离
    distance =sqrt((P.x-C.x)*(P.x-C.x)+ (P.y-C.y)*(P.y-C.y));
    // 判断是否符合要求 distance<=r 不符合则返回 否则进行运算
    if(distance<=r){
     printf("您输入的数值不在范围内!\n");
     return 0;
    }
     
    // 点p 到切点的距离
    length = sqrt(distance*distance-r*r);
    
    // 点到圆心的单位向量
    U.x=(C.x-P.x)/distance;
    U.y=(C.y-P.y)/distance;
    
    // 计算切线与点心连线的夹角
    angle = asin(r/distance);
    
    // 向正反两个方向旋转单位向量
    Q1.x = U.x * cos(angle)  -  U.y * sin(angle);
    Q1.y = U.x * sin(angle)  +  U.y * cos(angle);
    Q2.x = U.x * cos(-angle) -  U.y * sin(-angle);
    Q2.y = U.x * sin(-angle) +  U.y * cos(-angle);
    // 得到新座标
    Q1.x = ( Q1.x + P.x) * length;
    Q1.y = ( Q1.y + P.y) * length;
    Q2.x = ( Q2.x + P.x) * length;
    Q2.y = ( Q2.y + P.y) * length;
    // 输出坐标
    printf("Q1的坐标为：(%.1f,%.1f),Q2的坐标为：(%.1f,%.1f) \n",Q1.x,Q1.y,Q2.x,Q2.y);
    
    return 0;
}