题意:
一张n*m的表格上有一些格子有一些水晶球,两个人轮流进行游戏
每次选择一个有水晶球的格子,选择其中至少一个水晶球将它左移或者下移,不能出界
还有一些格子上有M(Meditations)或者P(pollutant sources),对应的作用为
当你选择的格子上有M时,若你选择移动 t 个水晶球,那么会将2*t 个水晶球平分到可以移动到的格子内
当t个水晶被移动到有P的格子上时,t 变成 [t/2] (向下取整)
(n,m)处一定有P,(n-1,m)处一定有M
任意含M(x,y)和含P(a,b)的格子的位置关系满足式子的值为奇数
无法操作的玩家输掉比赛,给定局势,询问先手胜负态
思路:
先分析给出的位置关系的式子,可以发现所有含有M的格子和含有P的格子的奇偶关系不同
如果没有M和P的设定,这个问题就是一个简单的阶梯博弈,只用考虑离终点的距离为奇数的点
含有P的位置离终点的距离一定为偶数,所有对答案没有影响
含有M的位置离终点的距离一定为奇数,它每次会将一个奇数步上的 t 变成偶数步上的2*t
一定可以选择其中的 t 重新移动到奇数步上,所以对答案同样没有影响
所以答案就是所有距离终点奇数步的格子的水晶数异或值
代码:
#include<cstdio>
using namespace std;
int n,m,T,k,x,y,w;
int main()
{
scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&m,&k);
int ans = 0 , t = (n^m);
while(k--){
scanf("%d%d%d",&x,&y,&w);
if((x^y^t)&1)ans^=w;
}scanf("%d",&k);while(k--)scanf("%*d%*d");
scanf("%d",&k);while(k--)scanf("%*d%*d");
printf("%s\n",ans?"win":"lose");
}return 0;
}








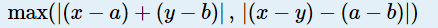














 872
872

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








