机器学习中的降维与度量学习(reduce dimension and metric learning)

##降维与度量学习
###k近邻学习
k近邻(k-Nearest Neighbor,简称kNN)学习是一种监督学习方法。
其工作机制为：在样本中，根据距离度量找出训练集中临近的k个样本，基于这k个样本进行预测。
一般，在分类任务中使用“投票法”，即选择最多的类别标记作为预测结果。
在回归任务中使用“平均法”。另外还可以使用距离度量以及加权平均来进行预测。
k近邻学习相比较其他的学习不同之处在于，它没有显式的训练过程。因此又称之为“懒惰学习”的代表。因为它在训练阶段只是保存样本，没有任何的时间开销，等到收到测试样本再进行学习。

k近邻学习中，参数k是很重要的，k的取值不同，会导致分类的结果不同。另外，如果采用不同的距离公式进行计算，则找出的“近邻”也是不同的，必然会导致分类结果差距变大。

接下来，我们取k=1来讨论，
给定测试样本x，若最近邻样本为z，则最近邻分类器出错的概率就是x与z类别标注不同的概率，即：

 假设样本独立同分布，且对任意x和任意小正数δ，在x附近δ距离范围内总能找到一个训练样本。 令c∗=argmaxP(c|x)表示贝叶斯最优分类器的结果。则有  我们通过上面的推导得出一个结论：最近邻分类器的泛化错误率不超过贝叶斯最优的分类器的两倍。 KNN在很多方面都有应用，其中大数据就是其中之一，至于为什么这么说，大家可以自由思考一下，就会懂得。 ###低维嵌入 引入的原因：由于学习方法很多都存在距离计算，但是高维空间会给这方面带来很大的麻烦。同时，在高维情形下出现的数据样本稀疏，距离计算困难时所有机器学习方法所面临的的困难，被称为“维数灾难”。 缓解维数灾难的一个重要途径就是“降维”(dimension reduction).即为通过一定的数学变换把高维空间变成一个低维的子空间，而这个子空间样本密度大幅度提高，距离计算也变得更容易。 能够降维的原因在于人们观察的高维样本，或许学习任务密切的却是某个低维分布，即高维空间中一个低维“嵌入”.  其中涉及到的维MDS算法进行降维：MDS算法的目的是使高维空间样本之间的距离在低维空间中得以保持。 假定m个样本在原始空间中任意两两样本之间的距离矩阵为D∈R(m*m)，我们的目标便是获得样本在低维空间中的表示Z∈R(d’*m , d’< d)，且任意两个样本在低维空间中的欧式距离等于原始空间中的距离，即||zi-zj||=Dist(ij)。因此接下来我们要做的就是根据已有的距离矩阵D来求解出降维后的坐标矩阵Z。   这时根据(1)–(4)式我们便可以计算出bij，即bij=(1)-(2)(1/m)-(3)(1/m)+(4)*(1/(m^2))，再逐一地计算每个b(ij)，就得到了降维后低维空间中的内积矩阵B(B=Z’*Z)，只需对B进行特征值分解便可以得到Z。MDS的算法流程如下图所示：  ###主成分分析(PCA) 主成分分析法(Principal Componet Analysis,简称PCA)是通过构建一个超平面，来将样本点映射到这个平面之上。但是这个平面需要满足两个条件：

• 最近重构性：样本点到这个超平面的距离尽量近;
• 最大可分性：样本点在超平面上的投影尽可能分开。

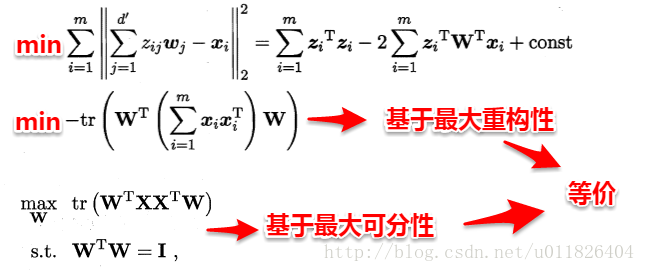
 使用拉格朗日乘子对式子进行优化：  最后，只需要对协方差矩阵进行特征值分解，即可得到解。PCA算法描述如下图所示：  在使用PCA方法进行降维之后，但是我们可能丢掉了一些特征值的特征值的特征向量，但是这是必须的，一方面，舍弃这方面信息增大了样本的密度；另一方面，也能达到去噪的效果。 PCA的应用： - Reduce memory/disk needed to store data.减少内存和磁盘需要储存的数据 - Speed up learning algorithm.加速学习的算法 - Visualization 可视化 ###核化线性降维 通常，线性降维方法假设是从高维空间到低维空间的函数映射是线性的，但是现实生活中仍然存在不少非线性映射。  基于这种情况的出现，我们使用非线性降维。非线性降维的一种常用方法，是基于核技巧 对线性降维方法进行“核化”。下面以核主成分分析(Kernelized PCA,简称KPCA)为例：   ###流形学习 流形学习(manifold learning)是一种借鉴了拓扑流形概念的降维方法。 ####等度量映射 等度量映射(Isometric Mapping,简称Isomap)主要是保持近邻样本距离不同。 基本出发点：高维空间中的直线距离具有误导性，因为有时高维空间中的直线距离在低维空间中是不可达的。因此利用流形在局部上与欧式空间同胚的性质，可以使用近邻距离来逼近测地线距离，即对于一个样本点，它与近邻内的样本点之间是可达的，且距离使用欧式距离计算，这样整个样本空间就形成了一张近邻图，高维空间中两个样本之间的距离就转为最短路径问题。可采用著名的Dijkstra算法或Floyd算法计算最短距离，得到高维空间中任意两点之间的距离后便可以使用MDS算法来其计算低维空间中的坐标。下图是Isomap算法描述：  对近邻图的构建的两种方法： 一、指定近邻点个数、如欧氏距离最近的k个点为近邻点，称之为k近邻图。 二、指定距离阈值。通过距离判断近邻点，即可得到近邻图。 但是两种方式存在着问题，分别会出现“断路”和“短路”问题。至于什么时候会出现问题，大家可以思考下。 #####局部线性嵌入 局部现象嵌入(Locally Linear Embedding,简称LLE)试图保持近邻样本的线性关系。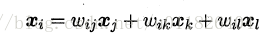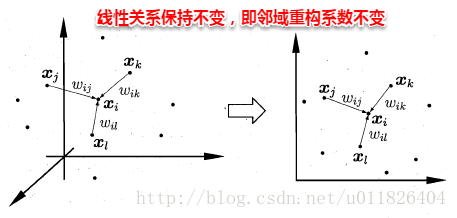 假定样本xi的坐标可以通过它的邻域样本线性表出：   LLE算法分为两步走，首先第一步根据近邻关系计算出所有样本的邻域重构系数w  接着根据邻域重构系数不变，去求解低维坐标,   这样利用矩阵M，优化问题可以重写为：  M特征值分解后最小的d’个特征值对应的特征向量组成Z，LLE算法的具体流程如下图所示：  ###度量学习 度量学习(metric learning)的基本动机：尝试“学习”得出一个合适的距离度量。这样就能减少找一个合适距离向量的时间开销。 首先要学习出距离度量必须先定义一个合适的距离度量形式。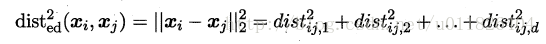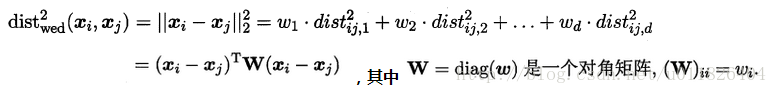对两个样本xi与xj，它们之间的平方欧式距离为：  若各个属性重要程度不一样即都有一个权重，则得到加权的平方欧式距离：  此时各个属性之间都是相互独立无关的，但现实中往往会存在属性之间有关联的情形，例如：身高和体重，一般人越高，体重也会重一些，他们之间存在较大的相关性。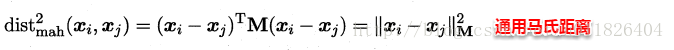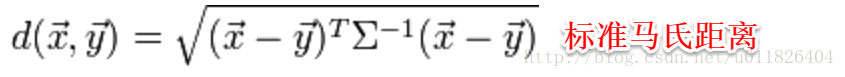这样计算距离就不能分属性单独计算，于是就引入经典的马氏距离(Mahalanobis distance):  标准的马氏距离中M是协方差矩阵的逆，马氏距离是一种考虑属性之间相关性且尺度无关（即无须去量纲）的距离度量:  矩阵M也称为“度量矩阵”，为保证距离度量的非负性与对称性，M必须为(半)正定对称矩阵，这样就为度量学习定义好了距离度量的形式，换句话说：度量学习便是对度量矩阵进行学习。现在来回想一下前面我们接触的机器学习不难发现：机器学习算法几乎都是在优化目标函数，从而求解目标函数中的参数. 总结：懒惰学习方法主要是k近邻学习器、懒惰决策树等。主成分分析是一种无监督的线性降维方法，监督线性降维方法就是线性判别分析(LDA)。 除了Isomap和LLE，常见的流形学习方法还有拉普拉斯特征映射、局部切空间对齐等。