问题描述:
给定n种物品和一个背包。物品i的重量是wi,其价值位vi ,背包的容量为C。问应该如何选择装入背包的物品,使得转入背包的物品的总价值为最大?
在选择物品的时候,对每种物品i只有两种选择,即装入背包或不装入背包。不能讲物品i装入多次,也不能只装入物品的一部分。因此,该问题被称为0-1背包问题。
把这个过程理解下,在前i件物品放进容量C的背包时,它有两种情况:
第一种是第i件不放进去,这时所得价值为:V[i-1][j]
第二种是第i件放进去,这时所得价值为:V[i-1][j-w[i]]+v[i] (容量j-w[i]里就要放进前i-1件物品)
状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。在上面的例子中状态就是前i件物品放入容量j的背包
定义了状态后,下面就是定义状态的转移
可以得出状态转移方程
V[i][j]=max{V[i-1][j],V[i-1][j-w[i]]+v[i]}
在这里使用一个(n+1)*(C+1)的表来计算V[i,j]的值
假设3个物品容量为5
w分别 1 ,2 ,3
v分别 6,10,12
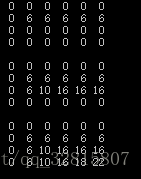
动态规划的过程如下
算法实现
#include <iostream>
#include <iomanip>
using namespace std;
int V[4][6];
int KNAPSACK(int n,int C,int w[],int v[]) {
for(int i=0; i<=n; i++) V[i][0]=0;
for(int j=0; j<=C; j++) V[0][j]=0;
for(int i=1; i<=n; i++){
for(int j=1; j<=C; j++) {
V[i][j]=V[i-1][j];
if(w[i-1]<=j)
V[i][j]=max(V[i][j],V[i-1][j-w[i-1]]+v[i-1]);
}
//(非必须)输出V数组显示动态规划的过程
for(int x=0; x<=n; x++){
for(int y=0; y<=C; y++){
cout<<setw(3)<<V[x][y];
}
cout<<endl;
}
cout<<endl;
}
//输出放入背包的物品
int k=C;
for(int i=n; i>=0; i--) {
if(V[i][k]>V[i-1][k]) {
cout<<v[i-1]<<" "<<w[i-1]<<endl;
k-=w[i-1];
}
}
//返回能装下的最大价值
return V[n][C];
}
int main() {
int n=4,C=6;
int w[3]={1,2,3};
int v[3]={6,10,12};
cout<<KNAPSACK(3,5,w,v);
return 0;
}优化
上面使用了二维数组来保存中间状态,我们也可以使用一维数组得到结果,也就是滚动数组
现在使用f[v]保存中间状态,我们想要达到的效果是,第i次循环后,f[v]中存储的是前i个物体放到容量v时的最大价值
f数组是从上到下,从右往左计算的。在计算f(i,j)之前,f[i]里保存的是上一个循环,也就是f(i-1,j)的值,而f[j-w]里保存的是f(i-1,j-w)的值。这里的重点是容量是逆序枚举的!
假设容量按照顺序枚举,来检测第 i 件物品是否能放。此时在执行第i次循环此时f[j-w]存储的是f(i,j-w)因为,v > v - w,第i次循环中f[j-w]中存储的实际是f(i,j-w)而非f(i-1,j-w)重点内容
int KNAPSACK()
{
memset(f,0,sizeof(f));
for (int i = 1;i <= n;i++)
{
for (int j = C;j >= w[i];j--) //逆序枚举容量!!
{
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
return f[C];
} 在递推法中,如果计算顺序很特殊,而且计算新状态所用到的原状态不多。可以尝试使用滚动数组减少内存开销,但滚动数组也有局限,例如打印方案较困难,当动态规划结束后,只有最后一个状态的值,而没有前面的值。
总结一下
根据上例分析和动态规划的基本概念,可以得到动态规划的基本模型如下:
(1)确定问题的决策对象。
(2)对决策过程划分阶段。
(3)对各阶段确定状态变量。
(4)根据状态变量确定费用函数和目标函数。
(5)建立各阶段状态变量的转移过程,确定状态转移方程。适用条件
任何思想方法都有一定的局限性,超出了特定条件,它就失去了作用。同样,动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和无后效性。
1.最优化原理(最优子结构性质) 最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。








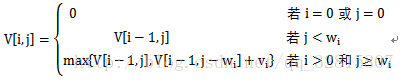














 349
349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








