动态规划——线性DP

所谓线性DP，就是递推方程是有一个明显的线性关系的，一维线性和二维线性甚至多维都有可能。
动态规划里的每一个状态都是一个多维(1-n维)的状态。
比如说背包问题就是一个二维的问题，如果我们把它画出来的话会是一个二维矩阵的形式。
而我们在求的时候，有一个明显的求的顺序：即一行一行地来求。这样的有线性顺序的叫做线性DP

题目1：数字三角形

AW898. 数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

这是一道DP初学者必接触的一道题，下面将通过陈列各种方法来说明DP的优越性。

方法一：简单递归，复杂度O(2^n)

方法二：记忆递归，复杂度O(n^2)

方法三：优化为递推，复杂度O(n^2)

优化思路：递归需要使用大量堆栈上的空间，容易造成栈溢出，所以换成递推

（主函数中的循环）：

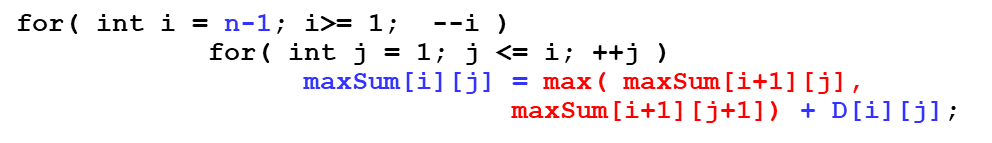
方法四：优化空间，复杂度O(n^2)

没必要用二维maxSum数组存储每一个MaxSum(r, j)。
只要从底层一行行向上递推，那么只要一维数组maxSum[500]即可,即只要存储一行的MaxSum值就可以。

int main(){    
	int i,j;    
	cin >> n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++)        
			cin >> D[i][j];   
			
	maxSum = D[n];   //maxSum指向第n行，是一个数组    
	for( int i = n-1; i>= 1;  --i )     
		for( int j = 1; j <= i; ++j )       
			maxSum[j] = max( maxSum[j],maxSum[j+1]) + D[i][j];    
			
	cout << maxSum[1] << endl;  
}

方法五：最终的DP代码，复杂度O(n^2)

yxc的分析方式如下图：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;

int n;
int a[N][N];
int dp[N][N];

int main()
{
    cin>>n;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            cin>>a[i][j];		
						//从1,1开始输入。0行和0列均被初始化为负无穷
    for (int i = 0; i <= n; i ++ )
        for (int j = 0; j <= i + 1; j ++ )
            dp[i][j] = -INF;

    dp[1][1] = a[1][1];		//确定初始状态的值
    for (int i = 2; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            dp[i][j] = max(dp[i - 1][j - 1] + a[i][j], dp[i - 1][j] + a[i][j]);//状态转移

    int res = -INF;
    for (int i = 1; i <= n; i ++ ) res = max(res, dp[n][i]); //遍历最后一层找最大

    cout<<res;
    return 0;
}

题目2：最长上升子序列

AW896. 最长上升子序列 II

本题可用DP做法解，但是时间复杂度是O(n²)，这复杂度挺高的，故略。
另外一种时间复杂度O(nlogn)的解法可供参考。

题目3：最长公共子序列

AW897. 最长公共子序列

动态规划问题分析：

集合的划分是按照 选或者不选a[i] , b[j] 为标准进行的状态划分

可以看到划分出来之后的表示方法仅仅只用 f 数组表示的话是会有交集的，但由于是求MAX，有交集不会受到影响。

还有值得注意的一点是初始状态的确定：
i==0时，A串为空，所以f[ 0 , j ]=0 即这一行都是0
同理，j==0时，f[ j , 0 ]=0 即这一列都是0
综上，输入字符串是由字符数组的1下标开始输入

AC代码如下

#include <iostream>
using namespace std;

const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    cin>>n>>m;
    cin>>a + 1>>b + 1;  //首地址

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);	//这两种情况的最大值的确定，是无论什么时候都存在的情况
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);	
            //此处的判断：当且仅当a[i] == b[j] 即它们对应位上相等的时候才有可能出现【a[i]和b[j]都选，长度加一】的可能
        }
        
    cout<<f[n][m]<<endl;
    return 0;
}

题目4：最短编辑距离

AW902. 最短编辑距离

动态规划问题分析：

依题意共有三种操作：删、增、改
分别用f 数组表示为：
删除的情况下：a串需要经过删最后一位来与b串相等，那就说明a的前i-1位可以与b完全匹配。即f[ i - 1 ][ j ]+1
增的情况下：a串需要经过增最后一位来与b串相等，那就说明b的前j-1位可以与a完全匹配。即f[ i ][ j - 1 ]+1
改的情况下：a串需要经过删最后一位来与b串相等，那就说明a的前i-1位可以与b-1位完全匹配。即f[ i - 1 ][ j - 1] + 1
但是改这种情况有特殊情况。因为f[ i - 1 ][ j - 1 ]分为a[ i ]与b[ j ]是否相等两种情况。如果相等则不用经过改步骤本身就是相匹配的，不需要+1。否则要进行“改”操作

AC代码如下

#include<iostream>
using namespace std;

const int N=1005;
int f[N][N];
int n,m;
char a[N],b[N];

int main()
{
    cin>>n>>a+1;
    cin>>m>>b+1;
    
    for(int i=0;i<=n;i++) f[i][0]=i;	//初始化（一个串为0的时候要增另一个串的长度次）
    for(int j=0;j<=m;j++) f[0][j]=j;
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            f[i][j]=min(f[i-1][j]+1,f[i][j-1]+1);
            if(a[i]==b[j]) f[i][j]=min(f[i][j],f[i-1][j-1]);
            else f[i][j]=min(f[i][j],f[i-1][j-1]+1);
        }
    cout<<f[n][m];
    
    return 0;
}

dp部分简写：

for (int i = 1; i <= n; i ++ )
	for (int j = 1; j <= m; j ++ )
    {
		f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
		f[i][j] = min(f[i][j], f[i - 1][j - 1]+(a[i]!=b[j]));
	}