//转自:http://www.oschina.net/code/snippet_203297_11313
组合数
组合数求模
组合数求模
问题:求解组合数C(n,m),即从n个相同物品中取出m个的方案数,由于结果可能非常大,对结果模10007即可。
方案1: 暴力求解,C(n,m)=n*(n-1)…(n-m+1)/m!,n<=15
方案2: 打表,C(n,m)=C(n-1,m-1)+C(n-1,m),n<=1,000
方案3: 质因数分解,C(n,m)=n!/(m!*(n-m)!),C(n,m)=p1a1-b1-c1p2a2-b2-c2…pkak-bk-ck,n<=10,000,000
方案4: Lucas定理,将m,n化为p进制,有:C(n,m)=C(n0,m0)*C(n1,m1)…(mod p),算一个不是很大的C(n,m)%p,p为素数,化为线性同余方程,用扩展的欧几里德定理求解,n在int范围内,修改一下可以满足long long范围内。
方案1
int Combination(int n, int m)
{
const int M = 10007;
int ans = 1;
for(int i=n; i>=(n-m+1); --i)
ans *= i;
while(m)
ans /= m--;
return ans % M;
}方案2
const int M = 10007;
const int MAXN = 1000;
int C[MAXN+1][MAXN+1];
void Initial()
{
int i,j;
for(i=0; i<=MAXN; ++i)
{
C[0][i] = 0;
C[i][0] = 1;
}
for(i=1; i<=MAXN; ++i)
{
for(j=1; j<=MAXN; ++j)
C[i][j] = (C[i-1][j] + C[i-1][j-1]) % M;
}
}
int Combination(int n, int m)
{
return C[n][m];
}方案3
//用筛法生成素数
const int MAXN = 1000000;
bool arr[MAXN+1] = {false};
vector<int> produce_prim_number()
{
vector<int> prim;
prim.push_back(2);
int i,j;
for(i=3; i*i<=MAXN; i+=2)
{
if(!arr[i])
{
prim.push_back(i);
for(j=i*i; j<=MAXN; j+=i)
arr[j] = true;
}
}
while(i<=MAXN)
{
if(!arr[i])
prim.push_back(i);
i+=2;
}
return prim;
}
//计算n!中素因子p的指数
int Cal(int x, int p)
{
int ans = 0;
long long rec = p;
while(x>=rec)
{
ans += x/rec;
rec *= p;
}
return ans;
}
//计算n的k次方对M取模,二分法
int Pow(long long n, int k, int M)
{
long long ans = 1;
while(k)
{
if(k&1)
{
ans = (ans * n) % M;
}
n = (n * n) % M;
k >>= 1;
}
return ans;
}
//计算C(n,m)
int Combination(int n, int m)
{
const int M = 10007;
vector<int> prim = produce_prim_number();
long long ans = 1;
int num;
for(int i=0; i<prim.size() && prim[i]<=n; ++i)
{
num = Cal(n, prim[i]) - Cal(m, prim[i]) - Cal(n-m, prim[i]);
ans = (ans * Pow(prim[i], num, M)) % M;
}
return ans;
}方案4
#include <stdio.h>
const int M = 10007;
int ff[M+5]; //打表,记录n!,避免重复计算
//求最大公因数
int gcd(int a,int b)
{
if(b==0)
return a;
else
return gcd(b,a%b);
}
//解线性同余方程,扩展欧几里德定理
int x,y;
void Extended_gcd(int a,int b)
{
if(b==0)
{
x=1;
y=0;
}
else
{
Extended_gcd(b,a%b);
long t=x;
x=y;
y=t-(a/b)*y;
}
}
//计算不大的C(n,m)
int C(int a,int b)
{
if(b>a)
return 0;
b=(ff[a-b]*ff[b])%M;
a=ff[a];
int c=gcd(a,b);
a/=c;
b/=c;
Extended_gcd(b,M);
x=(x+M)%M;
x=(x*a)%M;
return x;
}
//Lucas定理
int Combination(int n, int m)
{
int ans=1;
int a,b;
while(m||n)
{
a=n%M;
b=m%M;
n/=M;
m/=M;
ans=(ans*C(a,b))%M;
}
return ans;
}
int main(void)
{
int i,m,n;
ff[0]=1;
for(i=1;i<=M;i++) //预计算n!
ff[i]=(ff[i-1]*i)%M;
scanf("%d%d",&n, &m);
printf("%d\n",func(n,m));
return 0;
}容斥原理
LL solve (LL n, LL r)
{
vector<int> p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0)
{
p.push_back (i);
while (n % i == 0)
n /= i;
}
if (n > 1) p.push_back (n);
LL sum = 0;
for (int msk=1; msk<(1<<p.size()); ++msk)
{
LL mult = 1,
bits = 0;
for (int i=0; i<(LL)p.size(); ++i)
if (msk & (1<<i))
{
++bits;
mult *= p[i];
}
LL cur = r / mult;
if (bits % 2 == 1)
sum += cur;
else
sum -= cur;
}
return r - sum;
}
/*****************************************/
/**容斥原理过程**/
LL per;
void dfs(LL a,LL b,LL c)//a在数组中的起始位置,b含的个数,c公共质因子的个数
{
if(b==c)
{
LL t=m;
for(int i=0;i<c;i++) t/=s[i];
per+=qmod(t,n,1);
//per+=balabala; 这里就是求选取这么多个元素的情况数有多少种
}
else
{
for(int i=a;i<total;i++)
{
s[b]=num[i];
dfs(i+1,b+1,c);
}
}
}
LL DeMorgan()
{
LL ans = 0;//看具体情况
for(int i=1;i<=total;i++)
{
per=0;
dfs(0,0,i);
if(i&1) ans-=per;
else ans+=per;
}
return ans;
}莫比乌斯反演
设f为算术函数,f的和函数F为F(n)=∑d|nf(d),它是依据f的值决定的.是否存在一种用F求f的简单方法?这就是 莫比乌斯反演公式
莫比乌斯函数
μ(n)=⎧⎩⎨⎪⎪1(−1)r0,n=1,n=p1∗p2∗...∗pr,other
莫比乌斯函数是一个乘性函数
莫比乌斯函数的和函数
F(n)=∑d|nμ(d)
满足
F(n)=∑d|nμ(d)={10,n=1,n>1
莫比乌斯反演公式
对于
f与其和函数F(F(n)=∑d|nf(d))
形式一:
f(n)=∑d|nμ(d)F(n/d)
形式二:
f(n)=∑n|dμ(d/n)F(d)
注意有这样的两种形式,
int mobius(int n){
int m = 1;
for(int i=2;i*i<=n;i++){
if(n%i==0){
m*=-1;
int k = 0;
n/=i;
if(n%i==0) {m=0;break;}//某个素因子的幂大于1
}
}
if(n>1) m *= -1;
return m;
}
/*******************************************/
线性筛法预处理mobius函数
int prime[N],kp;
int Is_or[N],mu[N];
void Prime(){
int x;
mu[1]=1;
memset(Is_or,true,sizeof(Is_or));
for(int i=2;i<=n;i++){
if(Is_or[i]) prime[kp++]=i,mu[i]=-1;
for(int j=0;j<kp&&i*prime[j]<=n;j++){
x = i*prime[j];
Is_or[x]=false;
if(0==i%prime[j]) break;
mu[x] = -mu[i];
}
}
return ;
}一些特殊的数
卡特兰数
stirling数
默慈金数
就是从(0,0)到(n,0)中 只能向左/左上/左下走的方案数
(x,y)其中y>0
两种公式










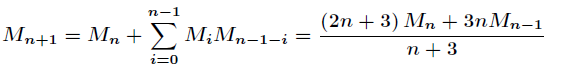
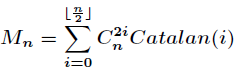














 266
266











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








