【概述】
容斥原理是一种较常用的计数方法,其基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复。
容斥原理核心的计数规则可以记为一句话:奇加偶减
假设被计数的有 A、B、C 三类,那么,A、B、C 类元素个数总和 = A 类元素个数 + B类元素个数 + C类元素个数 - 既是 A 又是 B 的元素个数 - 既是 A 又是 C 的元素个数 - 既是 B 又是 C 的元素个数 + 既是 A 又是 B 且是 C 的元素个数
即:A∪B∪C = A+B+C - AB - BC - AC + ABC

当被计数的种类被推到 n 类时,其统计规则即遵循奇加偶减。
容斥定理最常用于求 [a,b] 区间与 n 互质的数的个数,该问题可视为求 [1,b] 区间与 n 互质的个数减去 [1,a-1] 区间内与 n 互质的个数,故而可先对 n 进行因子分解,然后从 [1,b]、[1,a-1] 区间中减去存在 n 的因子的个数,再根据容斥定理,奇加偶减,对 n 的因子的最小公倍数的个数进行处理即可。
【实例】
一个班级有50名学生,进行一次语数英考试,有9人语文满分,12人数学满分,14人英语满分,又知有6人语文、数学同时满分,3人语文、英语同时满分、8人英语、数学同时满分,还有2人三门课全部满分,求:没有一门课满分的有几人?至少一门课满分的有几人?
由题意知: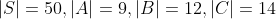 ,且:
,且: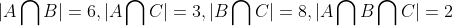
没有一门课满分的学生集合为: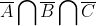 ,至少有一门课满分的学生集合为:
,至少有一门课满分的学生集合为: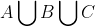
使用容斥原理:
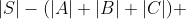
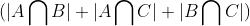
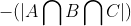
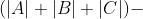
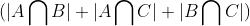
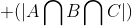
即:
【常见应用】
1.求[a,b]中与n互素的个数
问题可转换为区间 [1,b] 中与 n 互素的数的个数减去区间 [1,a-1]中与 n 互素的数的个数,那么问题就是转化为对于 n,求 1~k 中与 n 互质的数有多少个,因此可以先反着来求 1~k 中与 n 不互质的数有多少个。
故对n进行因子分解,然后从1~k中减去不能与n整除的数的个数,然后根据容斥定理奇加偶减,最后答案就是:1~b的元素个数减去1~a-1的元素个数再减去1~b中与n不互质的数的个数加上1~a-1中与n互质的数的个数。
即:b-(a-1)-calculate(b)+calculate(a-1)
bool bprime[N];
LL prime[N],cnt, factor[N],num;
void isprime() {//筛素数
cnt=0;
memset(bprime,false,sizeof(bprime));
for(LL i=2; i<N; i++) {
if(!bprime[i]) {
prime[cnt++]=i;
for(LL j=i*i; j<N; j+=i)
bprime[i]=true;
}
}
}
void getFactor(int n){
num=0;
for(LL i=0; prime[i]*prime[i]<=n&&i<cnt; i++) {
if(n%prime[i]==0) {//记录n的因子
factor[num++]=prime[i];
while(n%prime[i]==0)
n/=prime[i];
}
}
if(n!=1)//1既不是素数也不是合数
factor[num++]=n;
}
LL calculate(LL m,LL num) {
LL res=0;
for(LL i=1; i<(1<<num); i++) {
LL sum=0;
LL temp=1;
for(LL j=0; j<num; j++) {
if(i&(1<<j)) {
sum++;
temp*=factor[j];
}
}
if(sum%2)
res+=m/temp;
else
res-=m/temp;
}
return res;
}
int main() {
isprime();
LL a,b,n;
scanf("%lld%lld%lld",&a,&b,&n);
getFactor(n)
//容斥定理,奇加偶减,
LL res=(b-(a-1)-calculate(b,num))+calculate(a-1,num);
printf("%lld\n",res);
return 0;
}2.求[1,n]中能/不能被m个数整除的个数
对于任意一个数 a[i] 来说,我们能知道在 1-n 中有 n/a[i] 个数是 a[i] 的倍数,但这样将 m 个数扫一遍一定会用重复的数,因此需要用到容斥原理
根据容斥定理的奇加偶减,对于 m 个数来说,其中的任意 2、4、...、2k 个数就要减去他们最小公倍数能组成的数,1、3、...、2k+1 个数就要加上他们的最小公倍数,因此 m 个数就有 2^m 种情况,对于每种状态,依次判断由多少种数组成,然后再进行奇加偶减即可
根据容斥原理有:sum=从 m 中选 1 个数得到的倍数的个数-从 m 中选 2 个数得到的倍数的个数 + 从 m 中选 3 个数得到的倍数的个数 - 从 m 中选 4 个数得到的倍数的个数……
那么能被整除的个数就是 sum,不能被整除的个数就是 n-sum
LL GCD(LL a,LL b){
return !b?a:GCD(b,a%b);
}
LL LCM(LL a,LL b){
return a/GCD(a,b)*b;
}
LL a[N];
int main(){
LL n;
int m;
scanf("%lld%d",&n,&m);
for(int i=0;i<m;i++)
scanf("%lld",&a[i]);
LL sum=0;
for(int i=0;i<(1<<m);i++){//2^m种状态
LL lcm=1;
LL cnt=0;
for(int j=0;j<m;j++){
if(i&(1<<j)){//从m中选出j个数
lcm=LCM(lcm,a[j]);
cnt++;
}
}
if(cnt!=0){
if(cnt&1)//奇加
sum+=n/lcm;
else//偶减
sum-=n/lcm;
}
}
printf(%lld "%lld\n",sum,n-sum);
return 0;
}

























 952
952

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








