贝叶斯分析之利用逻辑回归对数据进行分类

最新推荐文章于 2024-04-06 00:00:00 发布

好运来2333

最新推荐文章于 2024-04-06 00:00:00 发布

阅读量2.2k

点赞数 1

分类专栏： MachineLearning

本文链接：https://blog.csdn.net/qq_33254870/article/details/100739640

版权

MachineLearning 专栏收录该内容

12 篇文章 7 订阅

订阅专栏

这一节主要将逻辑回归模型应用到莺尾花数据集进行分类

our features were measured from each sample: the length and the width of the sepals and petals, in centimeters.
数据集包含 Setosa、Versicolor 和 Virginica 3 个种类，这三个类别标签就是我们想要预测的量，即因变量。其中每个种类包含有 50 个数据，每个数据包含 4 种变量（特征），这 4 种变量就是我们要分析的自变量，分别是：花瓣长度、花瓣宽度、花萼长度和花萼宽度。

1. 从单变量说起

先看一个简单的问题：请利用花萼长度这一特征（自变量）来对 setosa 和 versicolor 两类（因变量）进行分类。

（1）读取两类数据

df = iris.query("species == ('setosa', 'versicolor')")
y_0 = pd.Categorical(df['species']).codes
x_n = 'sepal_length' 
x_0 = df[x_n].values

（2）查看一下数据格式
在这里插入图片描述
（3）建立逻辑回归模型

with pm.Model() as model_0:
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta = pm.Normal('beta', mu=0, sd=10)
    
    mu = alpha + pm.math.dot(x_0, beta)
    theta = pm.Deterministic('theta', 1 / (1 + pm.math.exp(-mu)))
    
    bd = pm.Deterministic('bd', -alpha/beta)
    
    yl = pm.Bernoulli('yl', p=theta, observed=y_0)

    start = pm.find_MAP()
    step = pm.NUTS()
    trace_0 = pm.sample(5000, step, start, nchains=1)

varnames = ['alpha', 'beta', 'bd']
pm.traceplot(trace_0, varnames)
plt.savefig('B04958_05_05.png', dpi=300, figsize=(5.5, 5.5))

这里需要注意两点：

变量 theta 表示什么？变量 theta 是对 mu 应用逻辑函数之后的值，表示 $p (y = 1 ∣ x)$ ;
变量 bd 表示什么？变量 bd 表示决策边界，位于决策左侧的 x 值属于类别0，位于决策右侧的 x 值属于类别1。
接下来证明为什么 bd = $-\frac{\alpha}{\beta}$ ?
假设分类出错的代价是对称的，即 p=0.5 决定着区分 0类与 1类，所以有：
$logistic(\alpha + \beta x_i) => 0 = \alpha + \beta x_i => x_i-\frac{\alpha}{\beta}$

在这里插入图片描述

（4）将后验的总结打印出来，然后将 bd 与通过另外一种方式得到的值进行比较
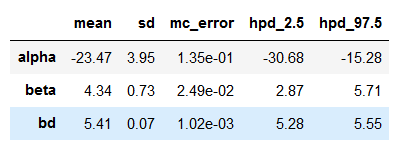
在这里插入图片描述

（5）现在我们将数据及拟合的Sigmoid曲线画出来
在这里插入图片描述

注意：这里的曲线是 $\frac{1}{1+e^{-(\alpha+\beta X)}}$ ，并不是 $\frac{1}{1+e^{-x}}$ 。
另外，上述模型找的决策边界95%HPD区间（红色区域）并不能很好地区分数据集。可能是模型不够好，也可能是只根据这一个特征很难区分这两个类别，显然这里应该是后者。

（6）使用模型做预测
给定若干个花萼长度返回他们分类结果为versicolor（1类）的概率值

def classify(n, threshold):
    """
    A simple classifying function
    """
    n = np.array(n)
    mu = trace_0['alpha'].mean() + trace_0['beta'].mean() * n
    prob = 1 / (1 + np.exp(-mu))
    return prob, prob >= threshold

classify([5, 5.5, 6], 0.5)

在这里插入图片描述
可以看到，三个样本点属于 1类的概率分别是（0.14， 0.59， 0.93）。

2. 多元逻辑回归

与多变量线性回归类似，多元逻辑回归使用了多个自变量。这里讲根据花萼长度与花萼宽度结合在一起对 setosa 与 versicolor 进行分类。
（1）读取两类数据

df = iris.query("species == ('setosa', 'versicolor')")
y_1 = pd.Categorical(df['species']).codes
x_n = ['sepal_length', 'sepal_width']
x_1 = df[x_n].values

#x_1 = (x_1 - x_1.mean(axis=0))/x_1.std(axis=0) 
#x_1 = (x_1 - x_1.mean(axis=0))

（2）查看一下数据格式
在这里插入图片描述
（3）建立逻辑回归模型

with pm.Model() as model_1:
    # We define the prioris
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta = pm.Normal('beta', mu=0, sd=2, shape=len(x_n))
    
    mu = alpha + pm.math.dot(x_1, beta)
    # Aplly the logistic linking function
    theta = 1 / (1 + pm.math.exp(-mu))
    # Compute the boundary decision
    bd = pm.Deterministic('bd', -alpha/beta[1] - beta[0]/beta[1] * x_1[:,0])
    
    # Define the likelihood
    yl = pm.Bernoulli('yl', p=theta, observed=y_1)
    # Sampling
    #start = pm.find_MAP()
    #step = pm.NUTS()
    #trace_1 = pm.sample(5000, step, start)
    trace_1 = pm.sample(5000, nchains=1)

chain_1 = trace_1[100:]
pm.traceplot(chain_1)
plt.savefig('B04958_05_07.png', dpi=300, figsize=(5.5, 5.5))

现在我们看看二元逻辑回归的决策边界（一条直线）：
$logistic(\alpha + \beta_0 x_0 + \beta_1 x_1) => 0 = \alpha + \beta_0 x_0 + \beta_1 x_1$ $x_1 = -\frac{\alpha}{\beta_1} + (-\frac{\beta_0}{\beta_1}) *x_0$