GNN基础知识

天狼啸月1990

已于 2024-06-09 17:31:36 修改

阅读量2k

点赞数 3

分类专栏： GNN algorithms 文章标签： GNN基础知识拉普拉斯矩阵切比雪夫多项式 attention 图傅里叶变换

于 2022-12-27 18:45:13 首次发布

本文链接：https://blog.csdn.net/qq_33419476/article/details/128458037

版权

GNN algorithms 专栏收录该内容

17 篇文章 1 订阅

订阅专栏

2. Jacobian Matrix雅克比矩阵

3. Laplacian matrix拉普拉斯矩阵

4. 图傅里叶变换 Graph Fourier Transformation

4.1 傅里叶变换 Fourier Transformation

4.2 谱分解 spectral decomposition (特征分解)

4.3 图傅里叶变换 Graph Fourier

5. 图卷积graph convolution

6. 切比雪夫多项式 Chebyshev polynomials

切比雪夫多项式

7. Attention Mechanism注意力机制

attention algorithm

attention 分类

torch self-attention

torch multi-head attention

8. Encoder-Decoder机制

9. Monte Carlo Approximation 蒙特卡洛近似

Examples of under-sampling and down-sampling

11. 交叉熵

12. 马尔科夫链Markov Chain和随机游走Random Walk

Markov Chain马尔科夫链

Random Walk on Graph图上随机游走

13. 高斯核函数(径向基RBF函数)

径向基神经元模型

高斯核函数codes

14. 欧式距离Euclidean Distance

1. 泰勒公式

背景background

有一个很复杂的方程，我们直接计算方程本身的值可能非常麻烦。

所以我们希望能够找到一个近似的方法来获得一个足够近似的值

本质: 近似，求一个函数的近似值

one point is 近似的方法
another point is 近似的精度
不断用线性方程相加：求导求斜率k， $\Sigma k*x$

泰勒公式原理

通过斜率逼近

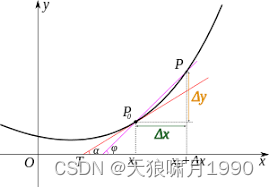
原理：经典的导数图，从上图可以看到，随着△x减小，间p0和点p也会越来越接近，这就带来了△y越来越接近△x·f'(x0)。

当然，当△x比较大时误差就会比较大，为了缩小误差，我们可以引入二阶导数、三阶导数以及高阶导数。由于最终不知道究竟要有多少阶导数，不妨假设f(x)在区间内一直有n+1阶导数。

To 与原值误差越来越小

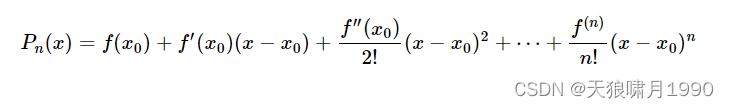
$p_{n}(x_{0}) \approx f(x_{0}) \\ p_{n}(x_{0}) \approx f(x_{0}) + f'(x_{0})(x-x_{0}) \\ p_{n}(x_{0}) \approx f(x_{0}) + f'(x_{0})(x-x_{0}) + f''(x_{0})\frac{(x-x_{0})^{2}}{2!}\\ .....$

分析

以导函数图为例，用f(x0)去近似f(x)，f(x0) + f'(x0)*(x-x0)，近似值与真实值之间仍然差着一小块误差e2: f(x) - f(x0) - f'(x0)(x-x0)，对于e2，继续用二阶导f''(x0)去加，去缩小f(x)-y'之间的误差。

2. Jacobian Matrix雅克比矩阵

假设F：Rn -> Rm是一个从n维欧式空间映射到m维欧式空间的函数，这个函数由m个实函数组成y1(x1,x2,...,xn),....,ym(x1,x2,...,xn)。这些函数的偏导数(如果存在)可组成一个m行n列的矩阵，即Jacobian matrix。

Meaning： $J_{F}(p)$ 这个线性映射即F在点p附近的最佳线性逼近。当x足够靠近p时，

$F(x) \approx F(p) + J_{F}(x-p)$

区别：

Jacobian matrix: 两个不同空间，点p逼近x
Taylor series approximation：同一空间中，点p逼近点x

3. Laplacian matrix拉普拉斯矩阵

本质：拉普拉斯矩阵 = Graph图拉普拉斯算子

拉普拉斯算子：n维欧式空间中的一个二阶微分算子，定义为梯度的散度。

$\Delta f = \sum_{i} \frac{\ni ^{2}f}{\ni^{2}xi}$

Meaning: 拉普拉斯算子计算了周围点与中心点的梯度差。

梯度gradient，矢量：该点处的导数沿该方向取得最大值，即变化率最大，可以简单理解为导数。
散度divergence，标量：表示空间中各点矢量场发散的强弱程度。

拉普拉斯矩阵L= 加权度矩阵D - 邻接矩阵A，对称矩阵

$L = \sum_{i\in Ni} \sum_{j\in Nj} W_{ij}f_{i} - \sum_{j\in Nj}W_{ij}f_{j}=D -A$

证明：用简单的一阶向量模拟矩阵去证明，不然展开计算太麻烦！

4. 图傅里叶变换 Graph Fourier Transformation

4.1 傅里叶变换 Fourier Transformation

Continuous 傅里叶变换：从空域spatial domain到谱域spectral domain；时域time到频域frequency

$F(w) = \frac{1}{2\pi } \int_{-\infty }^{\infty}f(t)e^{-iwt}dt$

Continuous 逆傅里叶变换：谱域到空域；从频域到时域

$f(x) = \int_{-\infty }^{\infty}F(w)e^{iwx}dw$

离散傅立叶变换 Discrete Fourier Transformation：

$\hat{x}(w) = \sum_{t=1}^{n}x(t) e^{-i\frac{2\pi}{n}wt}$

离散傅立叶逆变换 Inverse Discrete Fourier Transformation:

$x(t) = \frac{1}{n} \sum_{w=1}^n \hat{x}(w)e^{i\frac{2\pi}{n}wt}$

Meaning：

傅立叶变换的本质是：投影！求线性组合的系数。上面的傅里叶变换公式，将 $e^{-iwt}$ 看做一组(正交)基函数 base，则整个式子就是在算f(t)在 $e^{-iwt}$ 这个基上的投影坐标/系数 F(w)。
傅里叶逆变换本质是：线性组合！把任意一个函数表示成若干个正交基函数的线性组合！将函数f(t)拆解成无数个不同频率正弦波之和的过程，F(w)表示角频率为w的波的系数。

基base，类似x,y,z单位向量，组成的一个坐标系coordinate system，则对于任意一个3维向量，它都可以在改坐标系中写成坐标的形式(4,5,6)。

同理，傅里叶变换也是基于构建的基函数，通常是一组正交基，通过矩阵分解求得，f(t)在基坐标轴上的投影坐标，就是要求的F(w)，这里赋予他们特殊的物理学意义：角频率函数。

函数f(t)可以想象成一个长度为无穷的向量，函数空间中的内积定义为积分，上面的傅里叶变换公式，所有的w都要算一次，就可以得到f(t)在 $e^{-iwt}$ 这组基上的完整坐标，即F(w)。

理解内积定义为积分的操作：假设傅里叶变换可以写成[ $f_{t_1}*e^{-iwt_1} + f_{t_2}*e^{-iwt_2} +...+ f_{t_n}*e^{-iwt_n}$ ]，将无穷积分空间拆分成无数个细小的离散数值，t=-n...0,1,2,...n，而上面[0,n]区间的积分部分正好是matrix multiplication形式，即[ $f_{t_1}, f_{t_2},..., f_{t_n}$ ] * [ $e^{-iwt_1}, e^{-iwt_2},..., e^{-iwt_n}$ ]，即向量内积。

那如何将Fourier傅里叶变换与拉普拉斯算子联系起来？而这个基 $e^{-iwt}$ 恰好是拉普拉斯算子的特征向量。
那拉普拉斯算子如何与graph中的拉普拉斯矩阵联系起来呢？拉普拉斯算子和对于图信号而言，拉普拉斯矩阵是对于图Graph而言的，这两者有吸纳沟通的作用。-> 即拉普拉斯矩阵可以被认为是图上的拉普拉斯算子！ -》可以用拉普拉斯矩阵的特征向量作为图傅里叶投影的正交基！

4.2 谱分解 spectral decomposition (特征分解)

如何去求拉普拉斯矩阵Laplace Matrix L 的特征值 eigenvalues 和特征向量eigenvectors呢？

谱分解 spectral decomposition，即矩阵分解 Matrix Decomposition,求特征值和特征向量。基于特征向量的聚类称为谱聚类 spectral clustering，可以用于降维。

矩阵: $Ax = \lambda x -> (A-\lambda) x = 0$

- A是一个nxn实对阵矩阵；λ是矩阵A的特征值，x是特征值λ对应的特征向量。

Laplacian eigenvalues 特征值--担任了类似frequency的位置。
Laplacian eigenvectors 特征向量--担任了类似基函数的位置。

意义：特征值和特征向量可以用于表示原有复杂矩阵A，化简。这个过程称为特征分解Eigendecomposition，将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。

如果n个特征向量线性无关，那矩阵A就可以表示特征分表表示：

$A = W\Lambda W^{-1}$

其中， $\Lambda$ 为n个特征值λ为主对角线的对角矩阵nxn 对角矩阵diagonal matrix；W是n个特征列向量组成的nxn矩阵W={w1,w2,...,wn}。

一般来说，我们会把特征向量归一化||wi||2=1，即L2范数，正交化后的n个特征向量W变为标准正交基U，满足： $U^{T} U= I, -> U^{T}=U^{-1}$

正交矩阵： $U^{T}U = UU^{T} = I$
可逆矩阵： $U^{-1}U = UU^{-1} = I$
=》定理：正交矩阵的逆矩阵等于其转置矩阵。
=》拉普拉斯矩阵L可以写成特征分解形式: $L= U\Lambda U^{T}$ ，U是定义为n个正交化的特征列向量ui组成的一组正交基U=[ $u_1, u_2,...,u_n$ ]， $\Lambda$ 是n个特征值λi构成的对角矩阵，L是对称矩阵。

矩阵特征值和特征向量详细计算过程_矩阵特征向量怎么求_JunzeZhang的博客-CSDN博客

是不是matrix decomposition得到的特征向量可以直接用于图傅里叶变换了？

不，还需要矩阵正交化！通常只有正交化后的特征向量，才会被用作傅里叶变换的基。

方阵-QR正交分解: Q is the orthogonal matrix 正交矩阵, and R is an upper triangular matrix，斯密特正交化！酉矩阵即复数正交矩阵。
非方阵-奇异值分解: https://www.cnblogs.com/pinard/p/6251584.html

4.3 图傅里叶变换 Graph Fourier

傅里叶变换是以拉普拉斯算子的特征向量为基进行投影。

图傅里叶变换就是以拉普拉斯矩阵的特征向量正交基U进行投影，投影结果为向量x在正交空间中的坐标，或称为系数 $\hat{x}$ 。

图傅里叶变换：空间域 spatial domain-> 谱域 spectral domain；时域信号 signal x -> 频域frequency表示。可以定义为：

Graph Fourier Definition： $\hat{x} = U^{T}x$ ，

U表示拉普拉斯特征向量组成的正交基， $\hat{x}$ 中任一元素 $\hat{x}(\lambda_{i}) = \sum_{i=1}^{n}x(i)u_{l}(i)$

图傅里叶逆变换：谱域 -> 空间域；频域 -> 时域。可以定义为：

Inverse Graph Fourier Definition： $x=U\hat{x}$

为什么图傅立叶变换被定义为 $U^T x$ ，而不是 $xU$ ？

离散傅立叶变换： $\hat{x}(w) = \sum_{t=1}^{n}x(t) e^{-i\frac{2\pi}{n}wt}$ ，对比着看下面公式

我们定义一个列向量xi组成的图信号 $x=[x_1,x_2,...,x_n]$ ，则它的傅立叶变换为：

$F(\lambda_i) = \left \langle x, v_i \right \rangle = \sum_{j=1}^n x_j v_i(j)$ ，其中 $v_i(j)$ 表示第j个特征向量的第j个分量。

上式把拉普拉斯矩阵的特征值λi看成了频率，将图信号x投影到了该频率对应的特征向量上。这里的频率意义很难理解吧！反正我也没弄懂。

根据Fourier transformation变换定义，图信号x投影到一组特征向量(傅立叶正交基)上，得到一组傅立叶系数(即傅立叶正交基空间坐标)。而这个投影过程，就是傅立叶变换。

$\hat{x} = \left \langle x,v_k \right \rangle$ ，k=1,2,...,n

将傅立叶计算表示成矩阵形式：

$\hat{x} = \sum_{j=1}^n x_j v_i(j) = x_1v_1+x_2v_2+...+x_nv_n= (x_{1,1}v_{1,1}+x_{1,2}v_{1,2}+x_{1,3}v_{1,3}+..) + x_2v_2+...+x_nv_n=\begin{bmatrix} -v_1^T- \\ -v_2^T- \\ -...- \\ -v_n^T- \end{bmatrix} [x_1, x_2,...,x_n] = \begin{bmatrix} v_{1,1}^T, v_{1,2}^T,v_{1,3}^T,... \\ -v_2^T- \\ -...- \\ -v_n^T- \end{bmatrix}[\begin{vmatrix} x_{1,1} \\ x_{1,2} \\ x_{1,3} \\ ... \end{vmatrix}, x_2,...,x_n] = U^Tx$

当然，从纯计算的角度，DFT可以写成 $x^TU$ ，但谁让大家约定俗成用x表示呢！还把x写成列向量！

参考：图谱卷积预备知识2：图傅里叶变换-CSDN博客

为什么特征值λi能表示图信号的频率frequency呢？

图总变差total variation TV和拉普拉斯矩阵有非常直接的线性关系，权重是傅立叶系数的平方。

将所有特征值从小到大排列λ1,λ2,...,λn. 然后将上面问题转化为一个最优化问题：

$\left\{\begin{matrix} \lambda_1 = min xLx \\ s.t.x \in R^n, ||x||_2 = 1 \end{matrix}\right.$

因为总变差TV刻画的是图信号的全局平滑度，所以上式说明：更小的特征值对应的特征向量更平滑。所有特征值排列在一起，对图信号的平滑度做出了一种刻画。

=》因此我们可以将拉普拉斯的特征值等价成频率frequency！

=》特征值λi越小，其表示的频率就越低，对应的特征向量vi各个分量的变化就越缓慢，相近元素趋于一致。

参考：

图卷积网络原来是这么回事（二）——图傅里叶变换及案例分析 - 知乎

5. 图卷积graph convolution

Definition：图卷积跟数学中的卷积定义、CNN中的卷积本质上不是一个东西，它只是根据定义把频域乘积再变换回来的过程叫图卷积，它是一个直接定义的概念，而不是严格推导出来的。

图卷积

$f *_Gg=U(U^{T}f\odot U^{T}g)$

f,g都是向量，f表示input 图信号x，g表示卷积核，或叫做滤波器函数filter；U是拉普拉斯特征向量组成的正交基矩阵。 $\odot$ 表示element-wise product逐元素乘法，表示频域信号 $U^Tf$ 与滤波器filter函数逐元素乘法。

为什么将图卷积核/滤波器 graph filter g假设为一个对角矩阵？

就是将element-wise product逐元素乘法的操作 -》转换成矩阵乘积的形式！

因为信号的频域表示 $U^Tf$ 结果是一组傅立叶系数 $[\hat{f}_1,\hat{f}_2,...,\hat{f}_n]$ ，即信号f在正交基空间中的坐标。

element-wise product逐元素乘法的效果 = 对角矩阵 $(g_\theta(\Lambda) = diag(\lambda_i)) * U^Tf$

目的是对频域信号的每个频率成分进行独立的调整！

所以，我们定义graph filter $g_\theta = diag(U^{T}g) = g_\theta(\Lambda) = g_\theta(\lambda_i)$ 为一个对角矩阵。

谱域图卷积spectral graph convolution

$f *_Gg = Ug_\theta U^{T}f$

谱域图卷积层spectral convolutional layer

$H_{:,j}^{(k)} = \delta(\sum_{i=1}^{f_{k-1}}U\theta _{i,j}^{(k)}U^{T}H_{:,i}^{(k-1)})$

上式图卷积层表示

第k层有多个卷积核 $\theta _{i,j}^{(k)}$

第k层j channel的输入 = 第k-1层j channel的输出

第k-1层j channel的输出 = 第k-1层 i~fk-1 channel的输入 $H_{:,i}^{(k-1)}$ * 对应的第k层i -> j channel卷积核，求和 + 激活函数后，得到j channel输出。

参考：GNN Algorithms(2): GCN, Graph Convolutional Network_天狼啸月1990的博客-CSDN博客

6. 切比雪夫多项式 Chebyshev polynomials

逼近原理：直接计算太难，用比较简单的函数来近似代替原函数，且所产生的误差可以有量化的表征。
对任意n≥1的整数，有

$1 + C_{n}^{2} + C_{n}^{4} + ... = 2 ^{n-1}$

cos(nθ)

$cos 2\theta = 2cos\theta ^{2}-1 \\ cos4\theta = 2cos 2\theta ^{2} - 1 \\$

...

cos(nθ) = g(cosθ)，可以表示为cosθ的n次多项式，首项系数为 $2^{n-1}$

证明：利用棣莫弗公式(伏地魔公式)

$(cos \theta + isin\theta)^{n} = cos n\theta + isin n\theta$

切比雪夫多项式

$g(x) = cos(n\theta) = cos(narccosx)$ ，其中x=cosθ

所以，对于第一类切比雪夫多项式Tn(x)=cos(n·arccosx):

当n=0时，Tn(x)=1

当n=1时，Tn(x)=x

当n=2时，Tn(x)= $2x^{2}-1$

当n=3时，Tn(x)= $4x^{3}-3x$

当n=4时，Tn(x)= $8x^{4}-8x^{2}+1$

当n=5时，Tn(x)= $16x^{5}-48x^{4}+18x^{2}-1$

…

Tn+1(x)=2xTn(x)-Tn-1(x)

Meaning: 求函数在指定区间上最大值的最小值问题->最佳逼近！

7. Attention Mechanism注意力机制

background：RNN(50词)、LSTM(200词)长序列依赖问题、无法做并行计算

理论基础：类似于CNN中"感受野"receptive field的思想，attention mechanism从全部到只关注重点。

solution：self-attention，突破RNNs等序列sequence模型的固有缺陷，捕获长距离信息依赖，生成具有句法特征和语义特征的新向量。

句法特征。
语义特征。

优点：

解决了长距离依赖
可以并行。

缺点：

计算成本太高，有seq model O(n)的复杂度-> $O(n^{n})$ 计算复杂度。一般设置embedding维度在50左右。
既然可以并行，词与词之间不存在顺序关系，即无位置关系。-> 位置编码positional encoding

本质：加权求和。

权重矩阵Wq * Q = q1; Wk * K = k1; Wv * V = v1，这才是attention计算中的qkv。

q1通过与k1计算相似度，softmax后得到相似概率a1，也可以称为注意力概率，即k1代表的单词在q1单词新的向量表示中的占比，最后实现是通过加权就和，q1新的向量表示z1=a1*v1 + a2*v2。即长距离强相关的单词信息融入到q1新向量表示中，克服了RNN长距离相关单词在q1新向量表示中信息丢失的问题。

self-attention: QKV相乘(QKV同源)，QK相乘得到相似度A，AV相乘得到注意力值Z。

10 Transformer 之 Self-Attention（自注意力机制）_哔哩哔哩_bilibili

advantages：

参数少，less parameters。比CNN、RNN参数少复杂度低，算例要求低。
速度快，faster。可以并行处理。
效果好，more efficient。解决了长距离信息被弱化的问题。

缩放scale，避免未来做softmax的时候出现极端情况。

attention algorithm

Attention = (query, key, value)

1) Query和key进行相似度计算，得到权值weight

2) 将权值进行归一化，类似softmax，得到直接可用的归一化权重。

3) 将权重weight和value进行加权求和。

attention 分类

1) Soft-attention和Hard-attention: 是否将低概率weights重置为0，因为使用全部的weights纳入太多noise噪音数据，影响attention关注重点。

2) General-attention和Local-attention: 是否使用外部知识库或外部embedding。

-> self-attention: 当query=key=value时，即没有外部信息，那么在原文中的每个词可以跟该句子中的所有词进行Attention计算，相当于寻找原文内部的关系。

-> 通常情况下，self-attention在获取内部关系后，后面继续跟一个attention operation，与另外的句子执行attention操作。

3) Single-layer attention, multi-layer attention和multi-head attention: stacking multiple single-layer attention forms a multi-layer attention.

multi-head attention是采用多个query对同一段原文执行多次attention操作。

torch self-attention

import torch
import torch.nn as nn

class SelfAttention(nn.Module):
    def __init__(self, d_model, nhead):
        super(SelfAttention, self).__init__()
        self.d_model = d_model
        self.nhead = nhead
        self.query_linear = nn.Linear(d_model, d_model)
        self.key_linear = nn.Linear(d_model, d_model)
        self.value_linear = nn.Linear(d_model, d_model)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, input):
        # input: (batch_size, sequence_length, d_model)
        query = self.query_linear(input)
        key = self.key_linear(input)
        value = self.value_linear(input)
        
        # compute attention scores
        attention_scores = torch.matmul(query, key.transpose(-2, -1))
        attention_scores = attention_scores / torch.sqrt(torch.tensor(self.d_model, dtype=attention_scores.dtype))
        
        # apply softmax to get attention weights
        attention_weights = self.softmax(attention_scores)
        
        # compute the final attention output
        attention_output = torch.matmul(attention_weights, value)
        return attention_output

torch multi-head attention

8. Encoder-Decoder机制

编码器Encoder：顾名思义就是对输入句子X进行编码，将输入句子通过非线性变换转化为中间词义表示C：

C=F(x1, x2,...,xm)

解码器Decoder：其任务是根据句子X的中间词义表示C和之前已经生成的历史信息y1, y2,...,yi-1来生成i时刻要生成的单词yi：

Yi = g(c, Y1, Y2,...,Yi-1)

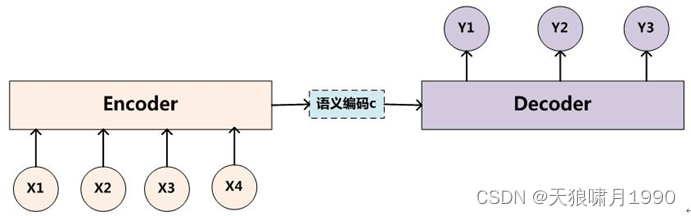
problems: 句子X中任意单词对生成某个目标单词yi来说影响力都是相同的，没有任何区别(其实如果Encoder是RNN的话，理论上越是后输入的单词影响越大，并非等权的，估计这也是为何Google提取Sequence to Sequence模型时发现把输入句子逆序输入做翻译效果更好的小trick原因)

solution: 在Encoder和Decoder之间引入Attention mechanism。原先都是通融的中间词义表示C会替换成根据当前生成单词而不断变化的Ci，即由固定的中间语义表示C换成了根据当前输出单词来调整成加入注意力模型的变化的Ci。

$C_{i} = \sum_{i=1}^{Tx}\alpha _{ij}h_{j}$

9. Monte Carlo Approximation 蒙特卡洛近似

本质：蒙特卡洛方法 -> 用近似来计算积分 -> 近似是通过采用sampling实现的，采样样本越多，就越逼近真实的积分效果。

background

大数定理：对于一个已知分布的随机序列，当取样数趋于无穷时，其均值趋向于期望。

$\frac{1}{n}\sum_{i=1}^{n}x_{i} \overset{p}{\rightarrow} u$ ，弱大数定律

当p=1时，强大数定律

中心极限定理：大量独立随机变量的和近似服从正态分布。其标准化：

$\frac{Y-E(Y)}{\sqrt{var(Y)}} = \frac{Y-nu}{\sqrt{n}u} ~ N(0,1) as n \rightarrow \infty$

期望：每次可能的结果*其结果概率的总和

pmf：probability mass function 离散概率分布

pdf：probability distribution function 连续概率分布

离散函数X的期望：

$E(X) = \sum_{i=1}^{n}pmf(x_{i}) * x_{i}$

连续变量X的期望：

$E(X) = \int _{-\infty }^{\infty}pdf(x_{i})*xdx$

估计连续变量的积分

$F(x) = \int_{a}^{b}f(x)dx$ 约等于f的蒙特卡洛积分 $F^{N} = \frac{1}{N}\sum_{i=1}^{N}\frac{f(x_{i})}{pdf(x_{i})}$

连续概率分布pdf(xi)=1/(b-a), 则1/pdf(xi)=(b-a)

证明：假设随机采样四个点x1,x2,x3,x4，并得到四个样本值f(x1), f(x2), f(x3), f(x4)

-> 有了这四个样本后，可以针对每一个样本求一个近似面积值f(xi)(b-a)来近似该函数在[a,b]段的积分。

因为每一个单独样本是原函数f(x)的近似，则每个样本f(xi)(b-a)让原函数曲线简化成一个矩形

$Area = \frac{1}{4}(b-a)\sum_{i=1}^{4}f(xi)$

-> 对于连续函数f，f每个可能的取值x的出现概率等于x的取值范围[a,b]的倒数1/(b-a)。

-> 蒙特卡洛积分≈连续函数的积分

-> 蒙特卡洛积分的期望 = 连续函数的积分

Monte Carlo Methods in Practice

10. pooling池化

Background

理论上，网络可以不对原始输入图像执行降采样操作，通过堆叠多个卷积层来构建深度神经网络，如此一来便可以在保留更多空间细节信息的同时提取到更具有判断力的抽象特征discriminative features。

注意Notice

池化层没有参数；一般在卷积过程后

作用

1) 保留主要特征的同时，减少参数和计算量，防止过拟合。

2) 扩大网络感受野

3) 抑制噪声，降低信息冗余，增强鲁棒性

up-sampling 上采样

旨在增加图像数据分辨率，多采样、高采样率

最近邻插值，nearest neighbor interpolation，复制最近像素填充新的像素位置
双线性插值，Bilinear interpolation，使用周围四个像素的加权平均来计算新的像素值，比最近邻插值更平滑。
双三次插值、亚像素卷积、转置卷积

down-sampling 下采样

即通常意义上的pooling池化操作！旨在降低图像数据分辨率，即减少数据、低采样率

top-k in the order of similarity.
最大池化，max pooling，取多个像素的最大值来代替，更关注局部特征，Max pooling with 2*2 filters and stride 步长2对一个4*4的featuremap进行扫描，选择最大值输出到下一层。
平均池化，average pooling，取多个像素的平均值来代替，更关注全局特征，将上述取某个区域的最大值改为求这个区域的平均值。
抽样，sampling，定期采样，每隔一个数据点采样一个数据。
overlapping pooling， stride < frame size ->提升预测精度，防止过拟合
低通滤波，low-pass filtering

over-sampling 过采样

over-sampling 过采样，For minority class, 插补 interpolation/伪造样本数据

over-sampling是增强少数类的样本，比如：SMOTE插值少数类样本来创建新的samples；采样概率与label number成反比，主要处理分类任务中的类别不平衡问题！能增加少数类样本数量，平衡数据集，改善模型对少数类的识别能力！可能因为增加了重复的数据导致过拟合，生成的数据可能引入noise，影响模型的性能。
区别 up-sampling：up-sampling是指时间序列或信号处理中的一个术语，指增加数据采样频率，从而在数据集中插入更多点，主要处理数据细化问题！可以使时间序列或信号更加精细，有助于捕捉数据的细节变化，提高模型性能！如果插值方法不当，可能会引入noise。

under-sampling 欠采样

under-sampling 欠采样，For majority class，删减多数类

under-sampling，采样概率与label number成反比，用于解决类别不平衡问题，减少多数类class的数量，使其与少样类样本数量更接近，如集成学习bagging，在多个欠采样集合上train model来提高模型性能。能有效平衡类别分布，减少model对多数类的偏见！可能会丢失重要信息，影响model performance。
区别 down-sampling：down-sampling是指减少数据采样率来降低数据的分辨率，常用于时间序列、图像或音频处理中。--》filtering noisy data，提高数据处理效率！可能丢失细节信息和重要特征，导致数据失真。

Examples of under-sampling and down-sampling

under-sampling example：假如我们有一个不平衡数据集，其中包含1000个多数类样本和100个少数类样本。通过随机欠采样，我们可以加少多数类样本，比如减少到100个，这样数据就变得平衡了。
down-sampling example：假如我们有一段每秒采样100次的时间序列数据，长度为10秒，总共有1000个数据点。通过下采样，我们可以减少采样率，绿如每秒采样10次，这样数据点总数减少到100.

11. 交叉熵

熵(entropy): 来源于热力学热量表征，现用于系统混乱程度的表征，越无序，熵越大。

熵增定律：科学家发现，一个东西放在那，不管它自己怎么运动，只会变得越来越混乱、无序，也就是说，熵只会越来越大。

孤立系统总是趋向于熵增，最终达到熵的最大状态，也就是系统的最混乱无序状态。但是，对开放系统而言，由于它可以将内部能量交换产生的熵增通过向环境释放热量的方式转移，所以开放系统有可能趋向熵减而达到有序状态。

二分类：

$L=\frac{1}{N}\sum_{i}L_{i}=\frac{1}{N}\sum_{i}-[yi*log(pi) + (1-yi)*log(1-pi)]$

Yi ->标志样本label，正类为1，负类为0

多分类

$L = \frac{1}{N}\sum_{i}Li=\frac{1}{N}\sum_{i}\sum_{c=1}^{M}y_{ic}log(p_{ic})$

12. 马尔科夫链Markov Chain和随机游走Random Walk

Markov Chain马尔科夫链

NP问题：Non-deterministic Polynomial非确定性多项式问题

Convergence：收敛

马尔科夫链：为状态空间经过从一个状态到另一个状态转换的随机过程。
马尔科夫性质：该过程具备"无记忆"性质，下一个状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。
在马尔科夫链的每一步，系统根据概率分布，可以从一个状态转变到另一个状态，也可以保持当前状态。

状态的改变叫转移，与不同的状态改变相关的概率叫转移概率transition probability

随机游走random walk是马尔科夫链的一个特殊例子
马尔科夫链是满足马尔科夫性质的随机变量x1, x2,...,即给出当前状态，将来状态和过去状态是相互独立的，从形式上看：

$p(X_{n+1}=x|X_{1}=x_{1}, X_{2}=x_{2},...,X_{n}=x_{n})=P(X_{n+1}=x|X_{n}=x_{n})$

Random Walk on Graph图上随机游走

concept：Given a graph and a starting point, we select a neighbor of it at random, and move to this neighbor; then we select a neighbor of this point at random, and move to it etc.

-> The random sequence of points selected this way is a Random Walk on the graph.

-> A random walk is a finite Markov chain that is time-reversible

-> 稳态向量 steady-state vector

$X = null(M-eye(6),'r') \\ Xs = X/sum(X)$

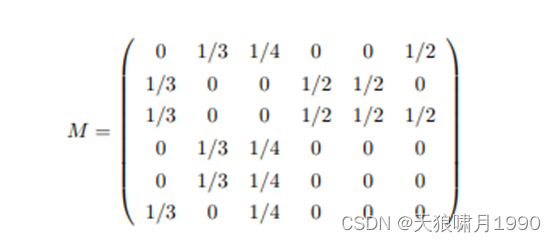
Null表示矩阵A的零空间，方程Ax=0的所有解V的集合，也叫A的核空间

eye(6)表示6阶单位矩阵，'r'表示特征值/实数向量

M表示随机游走的概率转移矩阵

13. 高斯核函数(径向基RBF函数)

本质是一个距离函数。

高斯核函数： $K(u)=\frac{1}{\sqrt{2\pi}} exp(- \frac{u^{2}}{2})$

核函数NWKernelRegression中的w参数是控制窗口大小的，用于控制核函数平滑度。

background: 非线性可分样本的分类？

用RBF作为隐单元的“基”构成隐藏层空间，隐藏层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。

高斯核函数(Gaussian kernel) ，最常用的径向基RBF函数(Radical Basis Function Kernel)

本质：高斯核本质是在衡量样本和样本之间的“相似度”，在一个刻画“相似度”的空间中，让同类样本更好的聚在一起，进而线性可分。

高斯核函数，用于将有限维数据映射到高维空间。通常定义为空间中任意一点x到某一中心点x'之间的欧氏距离的单调函数。

$k(x, x')=e^{- \frac{||x-x'||^{2}}{2\delta^{2}}}$

x'为核函数中心， $||x-x'||^{2}$ 为向量x和向量x'的欧式距离(L2范数)，随着两个向量的距离增大，高斯核函数单调递减。

δ用于控制高斯核函数的作用范围，其值越大，高斯核函数的局部影响范围就越大。(δ不要选太小，否则在分类任务中容易过拟合)

径向基神经元模型

单个神经元

在这里插入图片描述

神经网络模型

在这里插入图片描述

Reference：RBF神经网络理论与实现_风翼冰舟的博客-CSDN博客_rbf神经网络原理

高斯核函数codes

def RBF(x, L, sigma):
    '''
    x: 待分类的点的坐标 
    x': 中心点，通过计算x到x'的距离的和来判断类别
    sigma：有效半径
    '''
    return np.exp(-(np.sum((x - x') ** 2)) / (2 * sigma**2))