旋转矩阵
- 复数 z = a + b i z = a+bi z=a+bi可以看成一个向量 [ a b ] \begin{bmatrix} a \\ b \end{bmatrix} [ab],反过来,一个二维向量也可以看成一个复数。
- 复数
z
=
a
+
b
i
z=a+bi
z=a+bi也可以看成复平面上的一个点,在极坐标系下,
( a = r cos θ , b = r cos θ ) (a=r\cos \theta, b=r\cos\theta) (a=rcosθ,b=rcosθ),其中 θ \theta θ为幅角, r r r为模长,等于 ( a 2 + b 2 ) \sqrt{(a^2+b^2)} (a2+b2) - 现在我们考虑将一个向量
[
x
y
]
\begin{bmatrix} x \\ y \end{bmatrix}
[xy]旋转
θ
\theta
θ,怎么计算旋转之后的向量?
旋转之前的向量,用极坐标可以这么表示, α \alpha α为起始的幅角
{ x = r cos α y = r sin α \begin{cases} x = r\cos\alpha \\ y = r\sin\alpha \end{cases} {x=rcosαy=rsinα
旋转之后的向量,同样可以这么表示
{ x ′ = r cos ( α + θ ) y ′ = r sin ( α + θ ) \begin{cases} x' = r\cos(\alpha+\theta) \\ y' = r\sin(\alpha+\theta) \end{cases} {x′=rcos(α+θ)y′=rsin(α+θ)
把上述公式用和差化积展开
x ′ = r cos ( α + θ ) = r ( cos α cos θ − sin θ sin α ) = x cos θ − y sin θ \begin{equation} \begin{split} x' &= r\cos(\alpha+\theta)\\ &=r(\cos\alpha\cos\theta-\sin\theta\sin\alpha)\\ &=x\cos\theta-y\sin\theta \end{split} \end{equation} x′=rcos(α+θ)=r(cosαcosθ−sinθsinα)=xcosθ−ysinθ
y ′ = r sin ( α + θ ) = r ( sin α cos θ + cos α sin θ ) = x sin θ + y cos θ \begin{equation} \begin{split} y' &= r\sin(\alpha+\theta)\\ &=r(\sin\alpha\cos\theta+\cos\alpha\sin\theta)\\ &=x\sin\theta+y\cos\theta \end{split} \end{equation} y′=rsin(α+θ)=r(sinαcosθ+cosαsinθ)=xsinθ+ycosθ
整理一下,写成矩阵形式,
[ x ′ y ′ ] = [ cos θ − sin θ sin θ cos θ ] [ x y ] \begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} [x′y′]=[cosθsinθ−sinθcosθ][xy]
上述公式的 [ cos θ − sin θ sin θ cos θ ] \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} [cosθsinθ−sinθcosθ]就是我们所说的旋转矩阵
复数乘以复数
对于两个复数, z 1 = a + b i z_1=a+bi z1=a+bi和 z 2 = c + d i z_2=c+di z2=c+di,计算 z 1 z 2 z_1z_2 z1z2
- 矩阵视角
z 1 z 2 = ( a + b i ) ( c + d i ) = ( a c − b d ) + ( a d + b c ) i \begin{equation} \begin{split} z_1z_2 &=(a+bi)(c+di) \\ &=(ac-bd)+(ad+bc)i\\ \end{split} \end{equation} z1z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i
可以看成矩阵与向量的乘积,即
[ a − b b a ] [ c d ] \begin{bmatrix} a & -b\\ b & a \end{bmatrix} \begin{bmatrix} c\\ d \end{bmatrix} [ab−ba][cd] - 极坐标系视角
z 1 = r 1 ( cos θ 1 + i sin θ 1 ) z_1=r_1(\cos\theta_1+i\sin\theta_1) z1=r1(cosθ1+isinθ1)
z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z_2=r_2(\cos\theta_2+i\sin\theta_2) z2=r2(cosθ2+isinθ2)
z 1 z 2 = r 1 r 2 ( cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ) z_1z_2=r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)) z1z2=r1r2(cos(θ1+θ2)+isin(θ1+θ2))
可以看成将复数 z 1 z_1 z1旋转 θ 2 \theta_2 θ2,并且将模长缩放 r 2 r_2 r2。或者是将 z 2 z_2 z2旋转 θ 1 \theta_1 θ1,模长缩放 r 1 r_1 r1
旋转位置编码
目标:对q和k分别添加绝对位置信息,在做完点乘之后,具有相对位置信息。即q和k的位置分别是m,n,点乘之后,位置信息只与m-n有关
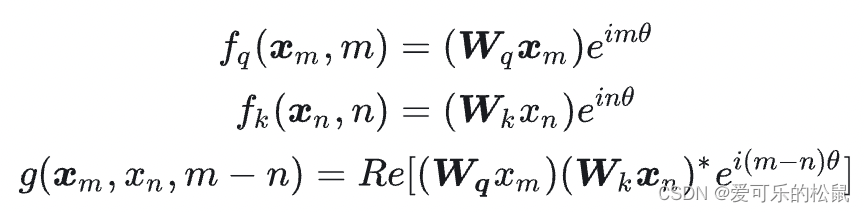
其中,
e
i
x
=
cos
x
+
i
sin
x
e^{ix}=\cos x+i\sin x
eix=cosx+isinx
W
q
,
W
k
W_q,W_k
Wq,Wk是quey和key对应的可学习矩阵,假设输入的query和key是
d
m
d_m
dm维的,那么
x
m
,
x
n
∈
R
d
m
×
1
x_m,x_n\in\mathcal{R}^{d_m\times1}
xm,xn∈Rdm×1,使用
W
q
,
W
k
W_q,W_k
Wq,Wk进行变换,变换之后的结果是
R
d
m
×
1
\mathcal{R}^{d_m\times1}
Rdm×1,这里我们只考虑2维的情况。
记
x
m
,
x
n
x_m,x_n
xm,xn变换之后的向量是
q
m
,
k
n
∈
R
2
×
1
q_m,k_n\in\mathcal{R}^{2\times1}
qm,kn∈R2×1。
q
m
e
i
m
θ
q_me^{im\theta}
qmeimθ是一个向量乘以一个复数,二维向量可以看成一个复数,那么上式可以看成两个复数相乘,那么根据第二部分的知识,两个复数的乘积等于:幅角相加,模长相乘。而
e
i
m
θ
e^{im\theta}
eimθ的模长是1,即相乘之后的模长不变,只进行了旋转,即把
q
m
q_m
qm向量旋转了
m
θ
m\theta
mθ角度。根据第一部分的知识,旋转就是乘上一个旋转矩阵,即
f
q
(
x
m
,
m
)
=
[
cos
m
θ
−
sin
m
θ
sin
m
θ
cos
m
θ
]
[
q
m
1
q
m
2
]
f_q(x_m,m)= \begin{bmatrix} \cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta \end{bmatrix} \begin{bmatrix} q_m^1 \\ q_m^2 \end{bmatrix}
fq(xm,m)=[cosmθsinmθ−sinmθcosmθ][qm1qm2]
f
k
(
x
n
,
n
)
=
[
cos
n
θ
−
sin
n
θ
sin
n
θ
cos
n
θ
]
[
k
n
1
k
n
2
]
f_k(x_n,n)= \begin{bmatrix} \cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta \end{bmatrix} \begin{bmatrix} k_n^1 \\ k_n^2 \end{bmatrix}
fk(xn,n)=[cosnθsinnθ−sinnθcosnθ][kn1kn2]
对于
q
m
k
n
∗
e
i
(
m
−
n
)
θ
q_mk_n^*e^{i(m-n)\theta}
qmkn∗ei(m−n)θ,前面的
q
m
k
n
∗
q_mk_n^*
qmkn∗可以看成两个复数相乘,可以转化为复数的矩阵形式,即
q
m
k
n
∗
=
[
q
m
1
−
q
m
2
q
m
2
q
m
1
]
[
k
n
1
−
k
n
2
]
=
[
q
m
1
k
n
1
+
q
m
2
k
n
2
q
m
2
k
n
1
−
q
m
1
k
n
2
]
\begin{equation} \begin{split} q_mk_n^*&= \begin{bmatrix} q_m^1 & -q_m^2\\ q_m^2 & q_m^1 \end{bmatrix} \begin{bmatrix} k_n^1 \\ -k_n^2 \end{bmatrix}\\ &= \begin{bmatrix} q_m^1k_n^1+q_m^2k_n^2 \\ q_m^2k_n1-q_m^1k_n^2 \end{bmatrix}\\ \end{split} \end{equation}
qmkn∗=[qm1qm2−qm2qm1][kn1−kn2]=[qm1kn1+qm2kn2qm2kn1−qm1kn2]
再乘上
e
i
(
m
−
n
)
θ
e^{i(m-n)\theta}
ei(m−n)θ,相当于把上述的2维向量旋转了
(
m
−
n
)
θ
(m-n)\theta
(m−n)θ,乘上一个旋转矩阵即可,即
q
m
k
n
∗
e
i
(
m
−
n
)
θ
=
[
cos
(
m
−
n
)
θ
−
sin
(
m
−
n
)
θ
sin
(
m
−
n
)
θ
cos
(
m
−
n
)
θ
]
[
q
m
1
k
n
1
+
q
m
2
k
n
2
q
m
2
k
n
1
−
q
m
1
k
n
2
]
\begin{equation} \begin{split} q_mk_n^*e^{i(m-n)\theta} &= \begin{bmatrix} \cos (m-n)\theta & -\sin (m-n)\theta \\ \sin (m-n)\theta & \cos (m-n)\theta \end{bmatrix} \begin{bmatrix} q_m^1k_n^1+q_m^2k_n^2 \\ q_m^2k_n1-q_m^1k_n^2 \end{bmatrix} \\ \end{split} \end{equation}
qmkn∗ei(m−n)θ=[cos(m−n)θsin(m−n)θ−sin(m−n)θcos(m−n)θ][qm1kn1+qm2kn2qm2kn1−qm1kn2]
只取实数部分,即
g
(
x
m
,
x
n
,
m
−
n
)
=
(
q
m
1
k
n
1
+
q
m
2
k
n
2
)
(
cos
(
m
−
n
)
θ
)
−
(
q
m
2
k
n
1
−
q
m
1
k
n
2
)
(
sin
(
m
−
n
)
θ
)
\begin{equation} \begin{split} g(x_m,x_n,m-n) &=(q_m^1k_n^1+q_m^2k_n^2) (\cos (m-n)\theta) - ( q_m^2k_n^1-q_m^1k_n^2)(\sin(m-n)\theta)\\ \end{split} \end{equation}
g(xm,xn,m−n)=(qm1kn1+qm2kn2)(cos(m−n)θ)−(qm2kn1−qm1kn2)(sin(m−n)θ)
对于
<
f
q
(
x
m
,
m
)
,
f
k
(
x
n
,
n
)
>
<f_q(x_m,m), f_k(x_n,n)>
<fq(xm,m),fk(xn,n)>,可以计算:
<
f
q
(
x
m
,
m
)
,
f
k
(
x
n
,
n
)
>
=
(
[
cos
m
θ
−
sin
m
θ
sin
m
θ
cos
m
θ
]
[
q
m
1
q
m
2
]
)
T
(
[
cos
n
θ
−
sin
n
θ
sin
n
θ
cos
n
θ
]
[
k
n
1
k
n
2
]
)
=
g
(
x
m
,
x
n
,
m
−
n
)
\begin{equation} \begin{split} <f_q(x_m,m), f_k(x_n,n)> &= \bigg( \begin{bmatrix} \cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta \end{bmatrix} \begin{bmatrix} q_m^1 \\ q_m^2 \end{bmatrix}\bigg)^T\bigg(\begin{bmatrix} \cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta \end{bmatrix} \begin{bmatrix} k_n^1 \\ k_n^2 \end{bmatrix}\bigg)\\ &=g(x_m,x_n,m-n) \end{split} \end{equation}
<fq(xm,m),fk(xn,n)>=([cosmθsinmθ−sinmθcosmθ][qm1qm2])T([cosnθsinnθ−sinnθcosnθ][kn1kn2])=g(xm,xn,m−n)
实现
根据上述的内容,我们可以发现,实现很容易,对query和key分别乘以一个旋转矩阵就可以了。对于多维的情况,两两分组即可。
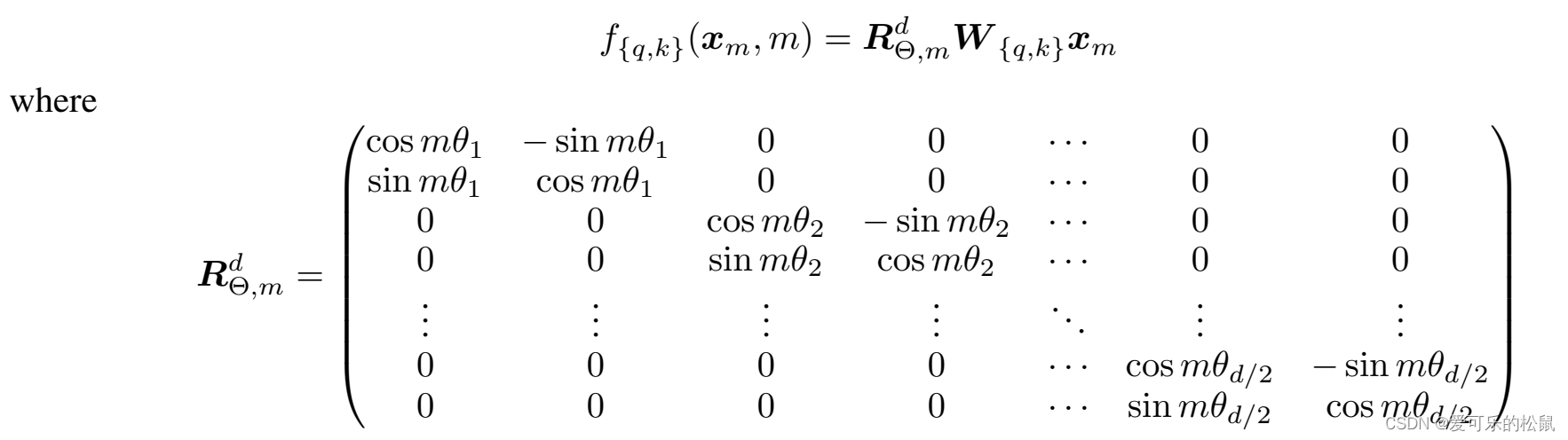
上述的矩阵过于稀疏,计算效率不高。因此有如下的高效实现
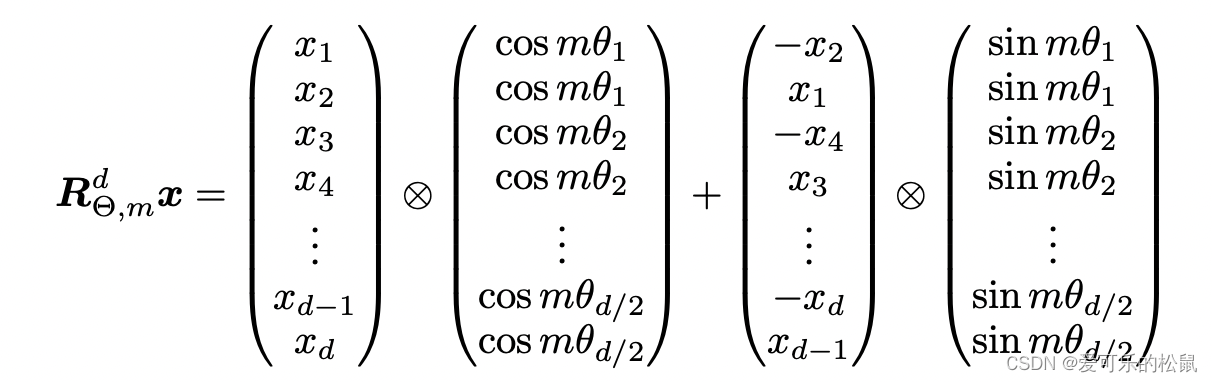
另外,transformers库中的实现与论文有点区别,高维的情况,不是相邻两个一组。





















 1128
1128

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








