t-SNE 降维可视化方法探索——如何保证相同输入每次得到的图像基本相同？

最新推荐文章于 2025-04-06 22:24:20 发布

Zy Fan

最新推荐文章于 2025-04-06 22:24:20 发布

阅读量7.3k

点赞数 7

分类专栏：神经网络踩坑记录文章标签：计算机视觉人工智能深度学习

本文链接：https://blog.csdn.net/qq_33548059/article/details/124835939

版权

神经网络踩坑记录专栏收录该内容

4 篇文章

订阅专栏

一、介绍

t-SNE是一种机器学习领域用的比较多的经典降维方法，通常主要是为了将高维数据降维到二维或三维以用于可视化。

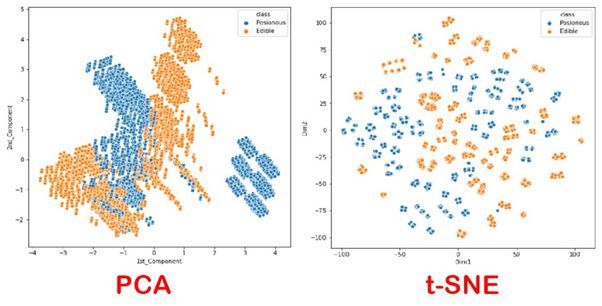
PCA 固然能够满足可视化的要求，但是人们发现，如果用 PCA 降维进行可视化，会出现所谓的“拥挤现象”。如下图所示，对于橙、蓝两类数据，如果我们用 PCA 降维后呈现在二维平面上，那么两类数据的边界并不明显，仿佛蓝色的数据“嵌入”了橙色数据一般。而反观右图，蓝色与橙色两类数据明显没有了交集。

How to Use t-SNE Effectivelyhttps://distill.pub/2016/misread-tsne/#perplexity=10&epsilon=5&demo=1&demoParams=50,2

二、t-SNE方法使用

需要提前install好一些依赖库，包括sklearn和matplotlib，都是很常用的库此处不再介绍安装和使用。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE


data = np.random.rand(64, 10)  # 64个样本，每个样本维度为10
target = np.arange(8).repeat(8)  # 生成64个标签，用于区分样本目标
t_sne_features = TSNE(n_components=2, learning_rate='auto', init='pca').fit_transform(data)
plt.scatter(x=t_sne_features[:, 0], y=t_sne_features[:, 1], c=target, cmap='jet')
plt.show()

data = np.random.rand(64, 10)  # 64个样本，每个样本维度为10
target = np.arange(8).repeat(8)  # 生成64个标签，用于区分样本目标
t_sne_features = TSNE(n_components=2, learning_rate='auto', init='pca').fit_transform(data)
plt.scatter(x=t_sne_features[:, 0], y=t_sne_features[:, 1], c=target, cmap='jet')
plt.show()

运行后得到下图：

由于这里原始数据分布就是random出来的，因此t-SNE后也是随机分布的。这里仅用于说明sklearn库中TSNE方法的使用和图像生成。

对于一些高维有聚类的数据（如神经网络的fc层特征）

可以看到一些聚类效果

三、参数说明

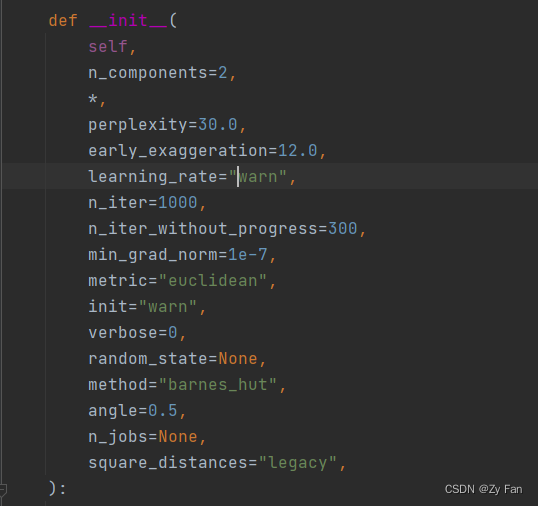
参数名称	参数含义
n_components	嵌入空间的维度
perpexity	混乱度，表示t-SNE优化过程当中考虑邻近点的多少，默认为30，建议取值在5到50之间
early_exaggeration	表示嵌入空间簇间距的大小，默认为12，该值越大，可视化后的簇间距越大
learning_rate	学习率，表示梯度降低的快慢，默认为200，建议取值在10到1000之间
n_iter	迭代次数，默认为1000，自定义设置时应保证大于250
min_grad_norm	若是梯度小于该值，则中止优化。默认为1e-7
metric	表示向量间距离度量的方式，默认是欧氏距离。若是是`precomputed`，则输入X是计算好的距离矩阵。也能够是自定义的距离度量函数。
init	初始化，默认为`random`。取值为`random`为随机初始化，取值为`pca`为利用PCA进行初始化（经常使用），取值为numpy数组时必须shape=(n_samples, n_components)
verbose	是否打印优化信息，取值0或1，默认为0=>不打印信息。打印的信息为：近邻点数量、耗时、 σ σ 、KL散度、偏差等
random_state	随机数种子，整数或`RandomState`对象
method	两种优化方法：`barnets_hut`和`exact`。第一种耗时O(NlogN)，第二种耗时O(N^2)可是偏差小，同时第二种方法不能用于百万级样本
angle	当method=`barnets_hut`时，该参数有用，用于均衡效率与偏差，默认值为0.5，该值越大，效率越高&偏差越大，不然反之。当该值在0.2-0.8之间时，无变化。

四、确保对于相同输入得到的图像相同方法

这也是记录本篇博客的核心原因。

由于需要在多次生成TSNE中对比效果，就需要保证对于相同输入tSNE生成的图像也基本分布一致。按照大部分网上资源的方法，最后的图虽然整体有序，但 对于同样的数据输入tSNE结果存在较大差异 ，比如相邻关系不变，但位置或者角度存在差异，大概情况如下图（举个例子说明）：

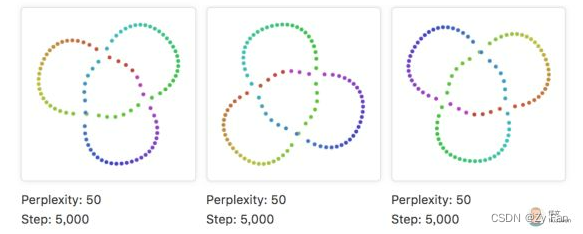
经过查阅官方文档参数意义以及多次尝试，发现最影响t-SNE图像的是随机数种子（也可以将其理解为是t-SNE训练的初始化情况，事实上t-SNE也是一种迭代训练的过程），对应接口函数中的参数为

random_state

随机数种子，整数或RandomState对象

因此，只需要在代码中指定random_state的值（如设定成2022）即可保证对于相同数据的降维情况一致，用于后续实验效果对比。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE


data = np.random.rand(64, 10)  # 64个样本，每个样本维度为10
target = np.arange(8).repeat(8)  # 生成64个标签，用于区分样本目标
t_sne_features = TSNE(n_components=2, learning_rate='auto', init='pca', random_state=2022).fit_transform(data)
plt.scatter(x=t_sne_features[:, 0], y=t_sne_features[:, 1], c=target, cmap='jet')
plt.show()

t_sne_features = TSNE(n_components=2, learning_rate='auto', init='pca', random_state=2022).fit_transform(data)
plt.scatter(x=t_sne_features[:, 0], y=t_sne_features[:, 1], c=target, cmap='jet')
plt.show()