S
x
S_x
Sx标准偏差=》作为标准误差是σ的估计值
因为我们无法知道真实的值A,所以我们是用的
x
ˉ
\bar{x}
xˉ近似A,然后
S
x
S_x
Sx所以分母从n调成了n-1,作为修正吧,使这个式子更近似。

S
x
ˉ
S_{\bar{x}}
Sxˉ 平均值的标准偏差 =》
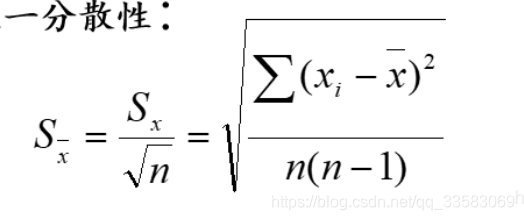
A类不确定度
u
A
(
x
ˉ
)
=
S
x
ˉ
=
1
n
∗
(
n
−
1
)
∑
i
=
1
n
(
X
i
−
x
ˉ
)
2
u_A(\bar{x})=S_{\bar{x}}=\sqrt{\frac{1}{n*(n-1)}\sum_{i=1}^n(X_i-\bar{x})^2}
uA(xˉ)=Sxˉ=n∗(n−1)1i=1∑n(Xi−xˉ)2
仪器的最大允许误差
Δ
m
\Delta_m
Δm = 置信区间的半宽度,(比方说分度值最小为0.1mm,则
Δ
m
=
0.05
m
m
\Delta_m = 0.05 mm
Δm=0.05mm)
包含因子k的取值:
| 正态分布 | 均匀分布 | 三角分布 |
|---|---|---|
| 3 | 3 \sqrt{3} 3 | 6 \sqrt{6} 6 |
B类不确定度
u
B
(
x
)
=
Δ
m
(
x
)
k
u_B(x) = \frac{\Delta_m(x)}{k}
uB(x)=kΔm(x)
标准不确定度的合成
u
C
(
x
)
=
u
a
2
(
x
ˉ
)
+
u
b
2
(
x
ˉ
)
u_C(x)=\sqrt{u_a^2(\bar{x})+u_b^2{(\bar{x})}}
uC(x)=ua2(xˉ)+ub2(xˉ)
最终结果写为
x
=
x
ˉ
±
u
c
(
x
)
x=\bar{x}\pm u_c(x)
x=xˉ±uc(x)
如果上述为正态分布,置信概率为68.3%
关于误差传递,我们把不确定度视为偏导数。
扩展不确定度:
u
A
(
x
ˉ
)
=
t
p
∗
S
x
ˉ
=
t
p
∗
1
n
∗
(
n
−
1
)
∑
i
=
1
n
(
X
i
−
x
ˉ
)
2
u_A(\bar{x})=t_p*S_{\bar{x}}=t_p*\sqrt{\frac{1}{n*(n-1)}\sum_{i=1}^n(X_i-\bar{x})^2}
uA(xˉ)=tp∗Sxˉ=tp∗n∗(n−1)1i=1∑n(Xi−xˉ)2
取值查下表:

数据处理规范:
一、平均值和实验标准差
无需列公式、带入原始数据求解。
平均值为所计算物理量的中间结果,可多保留1位有效数字。
实验标准差为不确定度的中间结果,保留3位有效数字。
二、计算
写出公式、带入原始数据、逐步计算(包含中间过程)
三、常数
常数的选取位数应当比中间过程或中间结果的数据有效数字多1位。
四、有效数字的运算
中间过程多保留1位有效数字。
五、不确定度
扩展不确定度最终保留1位有效数字;相对保留2位,中间过程保留三位。
六、科学计数法(必须用)
首位是个位。






















 268
268

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










