Chapter 5 Velocity Kinematics and Statics

最新推荐文章于 2024-05-11 22:02:28 发布

好悬给我拽开线

最新推荐文章于 2024-05-11 22:02:28 发布

阅读量63

点赞数

文章标签：算法

本文链接：https://blog.csdn.net/qq_33673253/article/details/132779814

版权

在前一章中，我们看到了如何计算给定一组关节位置的机器人末端执行器框架的位置和方向。在这一章中，我们研究了从一组给定的关节位置和速度计算开链末端执行器 twist 的相关问题。

在我们将末端执行器扭转表示为V∈R6之前，从5.1节开始，让我们考虑这样一种情况，即末端执行器的构型由坐标 $x\in\mathbb{R}^m$ 的最小集合表示，速度由 $\dot{x}=dx/dt\in\mathbb{R}^m$ 给出。在这种情况下，正运动学可以写成

$x(t)=f(\theta(t)),$

其中θ∈Rn是关节变量的集合。根据链式法则，t时刻的时间导数是

$\begin{aligned}\dot{x}&=\frac{\partial f(\theta)}{\partial\theta}\frac{d\theta(t)}{dt}=\frac{\partial f(\theta)}{\partial\theta}\dot{\theta}\\&=J(\theta)\dot{\theta},\end{aligned}$

其中J(θ)∈Rm×n称为雅可比矩阵。雅可比矩阵表示末端执行器速度 $\dot{x}$ 对关节速度 $\dot{\theta}$ 的线性灵敏度linear sensitivity，它是关节变量θ的函数。

为了提供一个具体的例子，考虑一个2R平面开链（图5.1左），正运动学为

$\begin{array}{rcl}x_1&=&L_1\cos\theta_1+L_2\cos(\theta_1+\theta_2)\\x_2&=&L_1\sin\theta_1+L_2\sin(\theta_1+\theta_2).\end{array}$

两边对时间求导会得到

$\begin{matrix}\dot{x}_1&=&-L_1\dot{\theta}_1\sin\theta_1-L_2(\dot{\theta}_1+\dot{\theta}_2)\sin(\theta_1+\theta_2)\\\dot{x}_2&=&L_1\dot{\theta}_1\cos\theta_1+L_2(\dot{\theta}_1+\dot{\theta}_2)\cos(\theta_1+\theta_2),\end{matrix}$

它可以重新排列成一个形式为 $\dot{x}=J(\theta)\dot{\theta}$ 的方程:

$\left[\begin{array}{c}\dot{x}_1\\\dot{x}_2\end{array}\right]=\left[\begin{array}{cc}-L_1\sin\theta_1-L_2\sin(\theta_1+\theta_2)&-L_2\sin(\theta_1+\theta_2)\\L_1\cos\theta_1+L_2\cos(\theta_1+\theta_2)&L_2\cos(\theta_1+\theta_2)\end{array}\right]\left[\begin{array}{c}\dot{\theta}_1\\\dot{\theta}_2\end{array}\right].\quad(5.1)$

将J(θ)的两列分别写成J1(θ)和J2(θ)，末端速度(x)作为 $v_{tip}$ ，式(5.1)变为

$v_{\mathrm{tip}}=J_1(\theta)\dot{\theta}_1+J_2(\theta)\dot{\theta}_2.\quad\quad\quad\quad\quad(5.2)$

只要J1(θ)和J2(θ)不共线，通过选择适当的关节速度 $\dot{\theta}_1$ 和 $\dot{\theta}_2$ ，就可以在x1 - x2平面上产生任意方向的末端速度 $v_{tip}$ 。由于J1(θ)和J2(θ)依赖于关节值θ1和θ2，有人可能会问是否存在某种构型使得J1(θ)和J2(θ)共线。对于我们的例子，答案是肯定的:如果θ2是0◦或180◦那么，不管θ1的值是多少，J1(θ)和J2(θ)将共线，雅可比矩阵J(θ)成为一个奇异矩阵。因此，这样的构型被称为奇点 singularities ;它们的特点是机器人尖端无法在某些方向上产生速度。

现在让我们代入L1 = L2 = 1，并考虑机器人在两种不同的非奇异姿态:θ = (0,π/4)和θ = (0,3 π/4)。这两种构型下的雅可比矩阵J(θ)是

$J\left(\left[\begin{array}{c}0\\\pi/4\end{array}\right]\right)=\left[\begin{array}{cc}-0.71&-0.71\\1.71&0.71\end{array}\right]\quad\text{and}\quad J\left(\left[\begin{array}{c}0\\3\pi/4\end{array}\right]\right)=\left[\begin{array}{cc}-0.71&-0.71\\0.29&-0.71\end{array}\right].$

图5.1的右侧显示了θ2 = π/4构型的机器人。

雅可比矩阵的第i列 $J_i(\theta)$ 对应于当θi = 1且另一个关节速度为0时的尖端速度。这些末端速度(以及雅可比矩阵的列)如图5.1所示。

雅可比矩阵可以用来将关节的转速边界映射到 $v_{tip}$ 边界，如图5.2所示。

我们可以在θ1 - θ2平面上映射关节速度的单位圆，而不是像图5.2那样通过雅可比矩阵来映射关节速度的多边形。这个圆表示关节速度空间中的“等功”轮廓，其中执行器的总功被认为是关节速度的平方和。这个圆通过雅可比矩阵映射到叶尖速度空间中的一个椭圆，这个椭圆被称为可操纵性椭球体 manipulability ellipsoid(在我们的例子中，二维椭球体通常被称为椭圆。).图5.3显示了2R臂两种不同姿势的映射示例。当机械臂结构接近奇点时，由于尖端在一个方向上移动的能力丧失，椭圆坍缩为线段。

利用可操纵性椭球可以量化给定姿态与奇点的接近程度。例如，我们可以比较可操纵性椭球的主半轴和副半轴的长度，分别表示为 $l_{max}$ 和 $l_{min}$ 。椭球体越接近圆形，即比值 $l_{max}/l_{min}$ 越接近1，尖端越容易向任意方向移动，从而越远离奇点。

雅可比矩阵在静态分析中也起着核心作用。假设一个外力作用于机器人的尖端。需要多大的关节力矩来抵抗这个外力?

这个问题可以通过能量守恒 a conservation of power 来回答。假设用于移动机器人的功率可以忽略不计，则机器人尖端处测量到的功率必须等于关节处产生的功率。将机器人产生的尖端力矢量记为 $f_{tip}$ ，关节力矩矢量记为 $\tau$ ，则能量守恒需要:

$f_\mathrm{tip}^\mathrm{T}v_\mathrm{tip}=\tau^\mathrm{T}\dot{\theta},$

对于所有任意关节速度 $\dot{\theta}$ 。由于 $v_{\mathrm{tip}}=J(\theta)\dot{\theta}$ ，等式：

$f_\mathrm{tip}^\mathrm{T}J(\theta)\dot{\theta}=\tau^\mathrm{T}\dot{\theta}$

对所有可能的 $\dot{\theta}$ 都成立。（由于机器人处于平衡状态，关节速度 $\dot{\theta}$ 为0。这可以看作是当 $\dot{\theta}$ 趋于零时的极限情况。更正式地说，我们可以引用“虚功原理”，它处理的是无穷小的关节位移，而不是关节速度。）

这只能在

$\tau=J^{\mathrm{T}}(\theta)f_{\mathrm{tip}}.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(5.3)$

时成立。产生尖端力 $f_{tip}$ 所需的关节扭矩 $\tau$ 由上述方程计算。

对于我们的两连杆平面链的例子，J(θ)是一个依赖于θ的方阵。如果位形θ不是奇点，则J(θ)及其转置都是可逆的，则式(5.3)可得

$f_{\mathrm{tip}}=((J(\theta))^{\mathrm{T}})^{-1}\tau=J^{-\mathrm{T}}(\theta)\tau. \quad(5.4)$

使用上面的方程，现在可以确定，在相同的静力平衡假设下，需要什么样的输入扭矩来产生所需的尖端力,例如，机器人尖端以一个给定的法向力 a specified normal force 推墙所需的关节扭矩。

对于机器人在平衡状态下的给定姿态θ和一组关节扭矩限制，如

$\begin{aligned}&-1\text{Nm}\le\tau_1\le1\text{Nm},\\&-1\text{Nm}\le\tau_2\le1\text{Nm},\end{aligned}$

则可以利用式(5.4)得到图5.4所示的所有可能的末端力集合。

对于可操纵性椭球体，可通过雅可比矩阵转置逆 $J^T(\theta)$ 将τ1 - τ2平面上的单位圆“等力”轮廓映射到f1 - f2末端力平面上的椭球体来绘制力椭球体 force ellipsoid(见图5.5)。

力椭球说明了机器人在不同方向上产生力的容易程度。从可操纵性和力椭球面可以明显看出，如果很容易在给定方向上产生尖端速度，那么很难在同一方向上产生力，反之亦然（图5.6）。

事实上，对于给定的机器人配置，可操纵性椭球体的主轴与力椭球的对齐，力椭球的主半轴的长度是可操纵性椭球的主半轴的长度的倒数。

在奇点处，可操纵性椭球体塌陷为线段。另一方面，力椭球在与可操纵性椭球线段正交的方向（即，对齐连杆的方向）上变得无限长，并且在正交方向上变薄。举个例子，用胳膊提一个沉重的手提箱。如果你的手臂在重力下笔直下垂（肘部在奇点处完全伸直），这会容易得多，因为你必须支撑的力直接通过你的关节，因此关节不需要扭矩。只有关节结构承受载荷，而不是产生力矩的肌肉。可操纵性椭球在奇点处失去尺寸，因此其面积降至零，但力椭球的面积变为无穷大（假设关节可以支撑载荷！）。

在本章中，我们提出了导出一般开链的雅可比矩阵的方法，其中末端效应器的构型表示为T∈SE（3）并且其速度被表示为在固fixed base frame or the end effector body frame中的扭曲 twist V。我们还研究了Jacobian如何用于速度和静态分析，包括识别运动学奇点和确定可操纵性和力椭球。关于逆运动学、运动规划、动力学和控制的后面章节广泛使用了本章中介绍的雅可比和相关概念。

5.1 Manipulator Jacobian

在 2R 平面开放链示例中，我们看到，对于任何joint关节配置 θ，尖端速度向量 vtip 和关节速度向量 $\dot{\theta}$ 通过雅可比矩阵 J(θ) 线性相关，即 $v_{tip}=J(\theta)\dot{\theta}$ 。\

尖端速度vtip取决于尖端感兴趣的坐标，而这些坐标又决定了Jacobian的具体形式。例如，在最常见的情况下，vtip可以被视为六维twist，而对于纯定向设备（如手腕），vtip通常被视为末端执行器框架的角速度。对于vtip的其他选择导致雅可比矩阵的不同表述。我们从一般情况开始，把vtip取为六维扭转 twist V。

以下所有推导都是相同简单思想的数学表达式，具体体现在方程（5.2）中：给定机器人的配置θ，作为 $J(\theta)$ 第i列的6维向量 $J_i(\theta)$ 为 $\dot{\theta}_i=1$ 且所有其他关节速度为零时的扭曲 twist V。该扭曲的确定方式与上一章中确定的关节螺纹轴的方式相同，使用旋转关节的关节轴i上的点qi。唯一的区别是Jacobian的螺旋轴取决于关节变量θ，而第4章正向运动学的螺旋轴总是在θ=0的情况下。

我们将考虑的两种标准类型的雅可比矩阵：

满足 $\mathcal{V}_s=J_s(\theta)\dot{\theta},$ 的空间雅可比矩阵 $J_s(\theta)$ ，其中每列 $J_{si}(\theta)$ 对应于在固定空间框架{s}中表示的螺旋轴
满足 $\mathcal{V}_b=J_b(\theta)\dot{\theta},$ 的body雅可比 $J_b(\theta)$ ，其中每列 $J_bi(\theta)$ 对应于在末端执行器框架{b}中表达的螺杆轴。

5.1.1 Space Jacobian

在本节中，我们推导了开放链的关节速度矢 $\dot{\theta}$ 和末端执行器的空间扭曲Vs之间的关系。我们首先回顾线性代数和线性微分方程的一些基本性质：

考虑一个n连杆的开链，其正运动学表示为如下的指数积形式:

$T(\theta_1,\ldots,\theta_n)=e^{[\mathcal{S}_1]\theta_1}e^{[\mathcal{S}_2]\theta_2}\cdots e^{[\mathcal{S}_n]\theta_n}M.\quad(5.5)$

空间扭转Vs由 $[\mathcal{V}_s]=\dot{T}T^{-1}$ 给出，其中

计算 $\dot{T}T^{-1}$ 得到

$[\mathcal{V}_s]=[\mathcal{S}_1]\dot{\theta}_1+e^{[\mathcal{S}_1]\theta_1}[\mathcal{S}_2]e^{-[\mathcal{S}_1]\theta_1}\dot{\theta}_2+e^{[\mathcal{S}_1]\theta_1}e^{[\mathcal{S}_2]\theta_2}[\mathcal{S}_3]e^{-[\mathcal{S}_2]\theta_2}e^{-[\mathcal{S}_1]\theta_1}\dot{\theta}_3+\cdots.$

以上也可以用伴随映射表示为向量形式:

注意，v是n个空间扭曲 spatial twists 的总和

$\mathcal{V}_s=J_{s1}+J_{s2}(\theta)\dot{\theta}_1+\cdots+J_{sn}(\theta)\dot{\theta}_n,\quad\quad\quad(5.7)$

其中每个 $J_{si}(\theta)=(\omega_{si}(\theta),v_{si}(\theta))$ 显式依赖于关节值 $\theta\in\mathbb{R}^{n}$ ，i = 2，…， n。在矩阵形式中，

矩阵Js(θ)被称为固定(空间)坐标系中的雅可比矩阵，或者更简单地说是空间雅可比矩阵 space Jacobian。

Definition 5.1.

设n环开链的正运动学表示为指数积形式:

$T=e^{[\mathcal{S}_1]\theta_1}\cdots e^{[\mathcal{S}_n]\theta_n}M.\quad\quad\quad\quad(5.9)$

空间雅可比矩阵 $J_s(\theta)\in\mathbb{R}^{6\times n}$ 将关节速率向量 $\dot{\theta}\in\mathbb{R}^n$ 与空间扭转Vs联系起来，通过：

$\mathcal{V}_s=J_s(\theta)\dot{\theta}.\quad\quad\quad\quad\quad\quad(5.10)$

$J_s(\theta)\in\mathbb{R}^{6\times n}$ 的第i列是

$J_{si}(\theta)=\mathrm{Ad}_{e^{[\mathcal{S}_1]\theta_1}\cdots e^{[\mathcal{S}_{i-1}]\theta_{i-1}}}(\mathcal{S}_i) \quad(5.11)$

对于i = 2，…， n，第一列 $J_{s1}=\mathcal{S}_1.$

为了理解 $J_{s}(\theta)$ 列背后的物理意义，观察第i列的形式为 $\mathrm{Ad}_{T_{i-1}}(\mathcal{S}_{i})$ ，其中 $T_{i-1}=e^{[\mathcal{S}_{1}]\theta_{1}}\cdots e^{[\mathcal{S}_{i-1}]\theta_{i-1}}$ 。回想一下，Si是根据机器人处于零位置的固定框架描述第i个关节轴的螺杆轴。因此， $\mathrm{Ad}_{T_{i-1}}(\mathcal{S}_{i})$ 是描述刚体位移Ti−1后第i个关节轴的螺钉轴。

从物理上讲，这与将前i−1关节从它们的零位置移动到当前值θ1，…，θi-1是一样的。因此， $J_{s}(\theta)$ 的第i列 $J_{si}(\theta)$ 仅仅是描述关节轴i的螺旋向量，在固定坐标系中表示为关节变量θ1，…,θi−1的函数。

总之，确定 $J_{s}(\theta)$ 的列 $J_{si}(\theta)$ 的过程类似于在指数乘积公式 $e^{[\mathcal{S}_1]\theta_1}\cdots e^{[\mathcal{S}_n]\theta_n}M$ 中推导关节螺旋Si的过程:每列 $J_{si}(\theta)$ 是描述关节轴i的螺旋向量，用固定坐标系表示，但对于任意θ而不是θ = 0。

Example 5.2 (Space Jacobian for a spatial RRRP chain).

现在我们将演示为图5.7中的空间RRRP链寻找空间雅可比矩阵的过程。

用 $J_{si}=(\omega_{si},v_{si})$ 表示 $J_{s}(\theta)$ 的第i列。 $[\mathrm{Ad}_{T_{i-1}}]$ 矩阵隐含在我们对位移关节轴的螺旋轴的计算中。

观察到 $\omega_{s1}$ 是常数，并且在zs方向上： $\omega_{s1}=(0,0,1)$ 。选择q1作为原点， $v_{s1}=(0,0,0)$ 。
ωs2在zs方向上也是常数，因此ωs2=（0，0，1）。选择q2作为点（L1c1，L1s1，0），其中c1=cosθ1，s1=sinθ1。则vs2=-ω2×q2=（L1s1，−L1c1，0）。
ωs3的方向总是固定在ω z方向，无论θ1和θ2的值如何，因此ωs3 =(0,0,1)。选择q3 = (L1c1 +L2c12, L1s1 +L2s12, 0)，其中c12 = cos(θ1 + θ2)， s12 = sin(θ1 + θ2)，则vs3 = (L1s1 +L2s12，−L1c1−L2c12, 0)。
由于最后的关节是移动的，ωs4 =(0,0,0)，关节轴方向由vs4 =(0,0,1)给出。

空间雅可比矩阵是

$J_s(\theta)=\left[\begin{array}{cccc}0&0&0&0\\0&0&0&0\\1&1&1&0\\0&L_1\text{s}_1&L_1\text{s}_1+L_2\text{s}_{12}&0\\0&-L_1\text{c}_1&-L_1\text{c}_1-L_2\text{c}_{12}&0\\0&0&0&1\end{array}\right].$

Example 5.3 (Space Jacobian for a spatial RRPRRR chain).

现在我们推导图5.8空间RRPRRR链的空间雅可比矩阵。base frame 的选择如图所示。

第一个关节轴在ωs1 =(0,0,1)的方向上。选择q1 = (0,0, L1)，我们得到vs1 = - ω1 × q1 =(0,0,0)。
第二个关节轴在ωs2 =(−c1，−s1, 0)的方向，选择q2 = (0,0, L1)，我们得到vs2 =−ω2 × q2 = (L1s1，−L1c1, 0)。
第三个关节是移动关节，所以ωs3 =(0,0,0)，移动关节轴的方向由 $v_{s3}=\operatorname{Rot}(\hat{\mathrm{z}},\theta_1)\operatorname{Rot}(\hat{\mathrm{x}},-\theta_2)\left[\begin{array}{c}0\\1\\0\end{array}\right]=\left[\begin{array}{c}-\operatorname{s_1c_2}\\c_1c_2\\-\operatorname{s_2}\end{array}\right].$
现在考虑手腕 wrist 部分。手腕中心位于这一点上 $q_w=\left[\begin{array}{c}0\\0\\L_1\end{array}\right]+\operatorname{Rot}(\hat{\mathrm{z}},\theta_1)\operatorname{Rot}(\hat{\mathrm{x}},-\theta_2)\left[\begin{array}{c}0\\L_2+\theta_3\\0\end{array}\right]=\left[\begin{array}{c}-(L_2+\theta_3)\text{s}_1\text{c}_2\\(L_2+\theta_3)\text{c}_1\text{c}_2\\L_1-(L_2+\theta_3)\text{s}_2\end{array}\right].$
观察腕轴的方向取决于θ1 θ2和先前的腕关节轴，有： $\begin{array}{rcl}\omega_{s4}&=&\operatorname{Rot}(\hat{\mathrm{z}},\theta_1)\operatorname{Rot}(\hat{\mathrm{x}},-\theta_2)\left[\begin{array}{c}0\\0\\1\end{array}\right]=\left[\begin{array}{c}-s_1s_2\\c_1s_2\\c_2\end{array}\right],\end{array}$ $\omega_{s5}\quad=\quad\operatorname{Rot}(\hat{z},\theta_1)\operatorname{Rot}(\hat{x},-\theta_2)\operatorname{Rot}(\hat{z},\theta_4)\left[\begin{array}{c}-1\\0\\0\end{array}\right]=\left[\begin{array}{c}-c_1c_4+s_1c_2s_4\\-s_1c_4-c_1c_2s_4\\s_2s_4\end{array}\right],$ $\begin{array}{rcl}\omega_{s6}&=&\operatorname{Rot}(\hat{\mathrm{z}},\theta_1)\operatorname{Rot}(\hat{\mathrm{x}},-\theta_2)\operatorname{Rot}(\hat{\mathrm{z}},\theta_4)\operatorname{Rot}(\hat{\mathrm{x}},-\theta_5)\left[\begin{array}{c}0\\1\\0\end{array}\right]\\\\&=&\left[\begin{array}{c}-c_5(s_1c_2c_4+c_1s_4)+s_1s_2s_5\\c_5(c_1c_2c_4-s_1s_4)-c_1s_2s_5\\-s_2c_4c_5-c_2s_5\end{array}\right].\end{array}$
空间雅可比矩阵现在可以计算并写成如下的矩阵形式:

注意我们可以直接得到整个雅可比矩阵，而不需要显式地微分正运动学映射。

5.1.2 Body Jacobian

在前一节中，我们推导了关节速率与 $[\mathcal{V}_s]=\dot{T}T^{-1},$ 之间的关系，末端执行器的扭转twist用固定帧坐标表示。在这里，我们推导出关节速率与 $[\mathcal{V}_b]=\dot{T}T^{-1},$ 之间的关系，末端执行器的twist在末端执行器坐标系坐标中表示。为此，将正运动学表示为指数形式的替代乘积将更方便：

$T(\theta)=Me^{[\mathcal{B}_1]\theta_1}e^{[\mathcal{B}_2]\theta_2}\cdots e^{[\mathcal{B}_n]\theta_n}.\quad(5.12)$

计算 $\dot{T}$

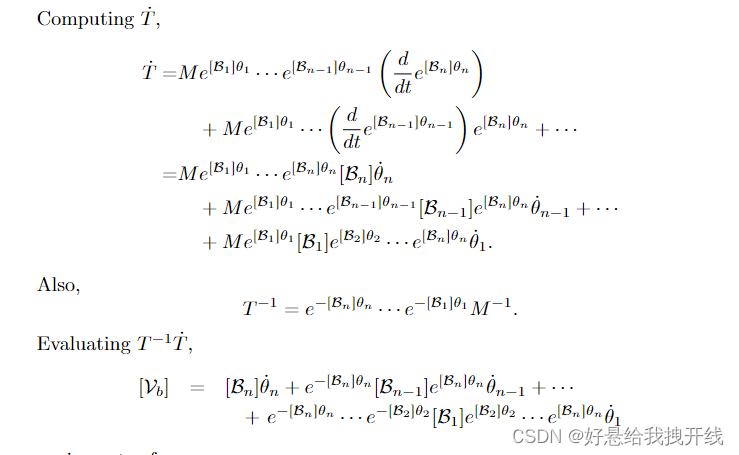
或者，以向量形式，

因此，扭转Vb可以表示为n个body twists的总和

$\mathcal{V}_b=J_{b1}(\theta)\dot{\theta}_1+\cdots+J_{bn-1}(\theta)\dot{\theta}_{n-1}+J_{bn}\dot{\theta}_n,\quad\quad(5.14)$

其中每个 $J_{bi}(\theta)=(\omega_{bi}(\theta),v_{bi}(\theta))$ 明确地依赖于 i = 1 ,..., n − 1的关节值 θ。在矩阵形式中，

$\mathcal{V}_b=\left[\begin{array}{cccc}J_{b1}(\theta)&\cdots&J_{bn-1}(\theta)&J_{bn}\end{array}\right]\left[\begin{array}{c}\dot{\theta}_1\\\vdots\\\dot{\theta}_n\end{array}\right]=J_b(\theta)\dot{\theta}.\quad(5.15)$

矩阵Jb(θ)是末端执行器(或身体)帧坐标中的雅可比矩阵，更具体地说，是身体雅可比矩阵 body Jacobian。

Definition 5.4.

设n连杆开放链的正向运动学用指数形式的下列乘积表示:

$T=Me^{[\mathcal{B}_1]\theta_1}\cdots e^{[\mathcal{B}_n]\theta_n}.\quad(5.16)$

身体雅可比矩阵 $J_b(\theta)\in\mathbb{R}^{6\times n}$ 将关节速率向量 $\dot{\theta}\in\mathbb{R}^{n}$ 与末端执行器扭转Vb = (ωb, vb)联系起来

$\mathcal{V}_b=J_b(\theta)\dot{\theta}.\quad(5.17)$

Jb(θ) 的第 i 列是

$J_{bi}(\theta)=\operatorname{Ad}_{e^{-(B_n)\theta_n}\ldots e^{-(B_{i+1})\theta_{i+1}}}(\mathcal{B}_i),\text{for}i=n-1,\ldots,1,\text{with}J_{bn}=\mathcal{B}_n.\quad(5.18)$

可以对Jb（θ）的列进行物理解释：

$J_b(\theta)$ 的每列 $J_{bi}(\theta)=(\omega_{bi}(\theta),v_{bi}(\theta))$ 是关节轴i的螺旋矢量，用末端执行器框架的坐标而不是固定框架的坐标表示。确定 $J_b(\theta)$ 列的程序类似于用指数乘积 $Me^{|\mathcal{B}_1|\theta_1}\cdots e^{|\mathcal{B}_n|{\theta}_n}$ 推导正向运动学的程序，唯一的区别是每个末端执行器框架关节螺钉 $J_{bi}(\theta)$ 表示为任意θ，而不是θ=0。

5.1.3 Visualizing the Space and Body Jacobian

另一种可能更简单的推导空间雅可比矩阵第i列（5.11）和身体雅可比矩阵第i列（5.18）公式的方法来自于图5.9中的5R机器人检查。让我们从空间Jacobian的第三列Js3开始，使用图5.9的左列。

当机器人处于其零配置时，对应于关节轴3的螺旋在{s}中被写成S3。显然，关节变量θ3、θ4和θ5对关节速度 $\dot{\theta}_3$ 产生的空间扭转 spatial twist 没有影响，因为它们没有使轴3相对于{s}发生位移。我们将关节变量固定为0，使从关节2向外的机器人为刚体B。如果θ1 = 0并且θ2是任意的，那么在 $T_{ss^{\prime}}=e^{[\mathcal{S}_{2}]\theta_{2}}$ 处的坐标系{s '}相对于B的位置和方向与在θ1 = θ2 = 0时的坐标系{s}相对B的相同。现在，如果θ1也是任意的，坐标系{s "}在 $T_{ss^{\prime\prime}}=e^{[\mathcal{S}_{1}]\theta_{1}}e^{[\mathcal{S}_{2}]\theta_{2}}$ 相对于B的位置和方向与坐标系{s}在θ1 = θ2 = 0时相对B的相同。因此，对于任意关节角θ1和θ2，S3表示相对于{s′′}的螺旋。然而，列Js3是相对于{s}的螺旋。将S3的表示帧从{s′′}改变为{s}的映射是 $[\mathrm{Ad}_{T_{ss^{\prime\prime}}}]=[\mathrm{Ad}_{e^{[\mathcal{S}_1]\theta_1}e^{[\mathcal{S}_2]\theta_2}}]$ ，即 $J_{s3}=[{\mathrm{Ad}}_{T_{ss}^{\prime\prime}}]\mathcal{S}_{3}$ ，精确地说，为关节i=3的等式（5.11）。式(5.11)是上述推理对任意关节i = 2，…，n的推广。

现在我们通过图5.9的右列来推导body Jacobian的第三列 $J_{b3}$ 。当机器人处于零位形时，关节3对应的螺旋记为{b}中的B3。变量θ1、θ2和θ3对关节速度 $\dot{\theta}_3$ 产生的身体扭转 body twist 没有影响，因为它们没有使轴3相对于{b}发生位移。我们将这些关节变量固定为0，使机器人从基座到关节4为刚体B。如果θ5 = 0并且θ4是任意的，那么在 $T_{bb^{\prime}}=e^{[\mathcal{B}_4]\theta_4}$ 处的坐标系{b '}是新的末端执行器坐标系。如果θ5也是任意的，那么坐标系{b "} 在 $T_{bb^{\prime\prime}}=e^{|\mathcal{B}_4|\theta_4}e^{|\mathcal{B}_5|\theta_5}$ 就是新的末端执行器坐标系。列Jb3是关节3的螺旋轴，用{b"}表示。由于B3用{b}表示，我们有

其中我们利用了 $(T_{1}T_{2})^{-1}=T_{2}^{-1}T_{1}^{-1}$ 。Jb3的这个公式正是关节joint i=3的方程（5.18）。方程（5.18）是上述推理对于任何 joint i=1，...，n-1的推广。

5.1.4 Relationship between the Space and Body Jacobian

用{s}表示固定框架，用{b}表示末端执行器框架，正向运动学可以写成 $T_{sb}(\theta)$ 。末端效应器框架的扭曲可以根据固定和末端效应器帧坐标写成

Vs和Vb由 $\mathcal{V}_s=\mathrm{Ad}_{T_{sb}}(\mathcal{V}_b)$ 和 $\mathcal{V}_b=\mathrm{Ad}_{T_{bs}}(\mathcal{V}_s)$ 相关。扭曲Vs和Vb也通过它们各自的雅可比矩阵相关:

因此式(5.19)可以写成

$\operatorname{Ad}_{T_{sb}}(\mathcal{V}_b)=J_s(\theta)\dot{\theta}.\quad\quad\quad\quad\quad(5.21)$

将 $[Ad_{T_{bs}}]$ 应用于式(5.21)的两边，利用伴随映射的一般性质 $[\mathrm{Ad}_X][\mathrm{Ad}_Y]=[\mathrm{Ad}_{XY}]$ ，得到

$\mathrm{Ad}_{T_{bs}}(\mathrm{Ad}_{T_{sb}}(\mathcal{V}_{b}))=\mathrm{Ad}_{T_{bs}T_{sb}}(\mathcal{V}_{b})=\mathcal{V}_{b}=\mathrm{Ad}_{T_{bs}}(J_{s}(q)\dot{\theta}).$

因为对于所有的 $\dot{\theta}$ ，我们也有 $\mathcal{V}_b=J_b(\theta)\dot{\theta}$ ，所以可以得出，Js(θ)和Jb(θ)是由

$J_{b}(\theta)=\mathrm{Ad}_{T_{bs}}\left(J_{s}(\theta)\right)=[\mathrm{Ad}_{T_{bs}}]J_{s}(\theta).\quad(5.22)$

空间雅可比矩阵又可由体雅可比矩阵通过

$J_{s}(\theta)=\operatorname{Ad}_{T_{sb}}(J_{b}(\theta))=[\operatorname{Ad}_{T_{sb}}]J_{b}(\theta).\quad(5.23)$

空间和体雅可比矩阵，以及空间和体扭曲，通过伴随映射类似地相关，这一事实并不奇怪，因为空间或体雅可比的每一列都对应于扭曲。

方程（5.22）和（5.23）的一个重要含义是Jb（θ）和Js（θ）总是具有相同的秩；这在关于奇异性分析的第5.3节中有明确的说明。

5.1.5 Alternative Notions of the Jacobian

上面导出的空间和身体雅可比矩阵是将关节速率与末端执行器的扭曲twist相关联的矩阵。存在基于使用坐标q的最小集合的末端执行器配置的表示的雅可比变换的替代概念。当任务空间被认为是SE（3）的子空间时，这种表示特别相关。例如，平面机器人末端执行器的配置可以被视为q=（x，y，θ）∈R3，而不是SE（2）的元素。

当使用最小坐标集时，末端执行器速度不是由扭曲V给出的，而是由坐标的时间导数 $\dot{q}$ 给出的，并且速度运动学 $\dot{q}=J_{a}(\theta)\dot{\theta}$ 中的Jacobian有时被称为解析Jacobian analytic Jacobian，而不是如上所述的空间和身体坐标系中的几何Jacobian geometric Jacobian

对于SE（3）任务空间，最小坐标q∈R6的典型选择包括固定帧中末端效应器帧的原点的三个坐标和固定帧中的末端效应器框架的方向的三个座标。方向的示例坐标包括欧拉角（见附录B）和旋转的指数坐标

Example 5.5 (Analytic Jacobian with exponential coordinates for rotation).

在这个例子中，我们发现了body frame中的几何Jacobian Jb和使用指数坐标 $r=\hat{\omega}\theta$ 来表示方向的解析Jacobian Ja之间的关系。（回想一下，θ∈[0，π]， $\|\hat{\omega}\|=1$ ）

首先，考虑一个具有n个关节的开链和体Jacobian

$\mathcal{V}_b=J_b(\theta)\dot{\theta},$

其中 $\begin{aligned}J_b(\theta)&\in\mathbb{R}^{6\times n}\end{aligned}$ 。Vb=（ωb，Vb）的角速度和线速度分量可以明确地写成

$\mathcal{V}_b=\left[\begin{array}{c}\omega_b\\v_b\end{array}\right]=J_b(\theta)\dot{\theta}=\left[\begin{array}{c}J_\omega(\theta)\\J_v(\theta)\end{array}\right]\dot{\theta},$

其中Jω是3 × n矩阵对应于Jb的上三行，Jv是3 × n矩阵对应于Jb的下三行。

现在假设我们的最小坐标集q∈R6由q = (r, x)给出，其中x∈R3是末端执行器坐标系原点的位置，r = ωθ∈R3是旋转的指数坐标表示。坐标时间导数 $\dot{x}$ 与vb的关系是通过旋转得到固定坐标下的vb:

$\dot{x}=R_{sb}(\theta)v_{b}=R_{sb}(\theta)J_{v}(\theta)\dot{\theta},$

其中 $R_{sb}(\theta)=e^{[r]}=e^{[\hat{\omega}]\theta}$

时间导数 $\dot{r}$ 与物体角速度ωb的关系如下 $\omega_b=A(r)\dot{r},$

其中 $A(r)=I-\frac{1-\cos\|r\|}{\|r\|^2}[r]+\frac{\|r\|-\sin\|r\|}{\|r\|^3}[r]^2.$

（这个公式的推导在练习5.10中进行了探索。）如果矩阵A（r）是可逆的，则可以从ωb得到 $\dot{r}$ ：

$\dot{r}=A^{-1}(r)\omega_b=A^{-1}(r)J_\omega(\theta)\dot{\theta}.$

把这些放在一起，我们得到

$\dot{q}=\left[\begin{array}{c}\dot{r}\\\dot{x}\end{array}\right]=\left[\begin{array}{cc}A^{-1}(r)&0\\0&R_{sb}\end{array}\right]\left[\begin{array}{c}\omega_b\\v_b\end{array}\right],\quad\quad(5.24)$

即解析雅可比 analytic Jacobian Ja与体雅可比body JacobianJb的关系如下

$J_a(\theta)=\left[\begin{array}{cc}A^{-1}(r)&0\\0&R_{sb}(\theta)\end{array}\right]\left[\begin{array}{cc}J_\omega(\theta)\\J_v(\theta)\end{array}\right]=\left[\begin{array}{cc}A^{-1}(r)&0\\0&R_{sb}(\theta)\end{array}\right]J_b(\theta).\quad(5.25)$

5.1.6 Looking Ahead to Inverse Velocity Kinematics

在上面的部分中，我们问了一个问题“给定的一组关节速度会产生什么扭曲？”答案是独立于扭曲所代表的框架而写的，由下式给出

$\mathcal{V}=J(\theta)\dot{\theta}.$

我们经常对相反的问题感兴趣：给定所需的扭曲V，需要什么样的关节速度 $\dot{\theta}$ ？这是一个逆速度运动学问题，第6.3节对此进行了更详细的讨论。简言之，如果J（θ）是平方的（因此关节的数量n等于六，即扭转的元素数量）并且是满秩的， $\dot{\theta}=J^{-1}(\theta)\mathcal{V}$ 。然而，如果 $n\neq 6$ 或机器人处于奇点，则J（θ）是不可逆的。在n<6的情况下，无法实现任意扭曲V——机器人没有足够的关节。如果n>6，则我们称机器人冗余 redundant 。在这种情况下，所需的扭曲V对关节速率施加了六个约束，剩余的n−6个自由度对应于机器人的内部运动，而这些运动在末端执行器的运动中并不明显。例如，如果你认为你的手臂从肩膀到手掌是一条七关节的开放链，当你将手掌放在空间中的固定配置（例如，在桌子表面）时，你仍然有一个与肘部位置相对应的内部自由度。

5.2 Statics of Open Chains

利用我们熟悉的功率守恒原理，我们有

关节处的功率 =（移动机器人的功率）+（末端执行器处的功率）、

并且，考虑到机器人处于静态平衡（没有使用动力来移动机器人），我们可以将关节处的动力等同于末端执行器处的动力（我们正在考虑当 $\dot{\theta}$ 变为零时的极限情况，这与我们假设机器人处于平衡状态一致。）: $\tau^\mathrm{T}\dot{\theta}=\mathcal{F}_{b}^\mathrm{T}\mathcal{V}_{b},$

其中τ是关节力矩的列矢量。利用恒等式 $\mathcal{V}_{b}=J_{b}(\theta)\dot{\theta}$ ，我们得到 $\tau=J_{b}^{\mathrm{T}}(\theta)\mathcal{F}_{b},$ 将关节扭矩与末端执行器坐标系中的wrench联系起来。同样在固定空间框架中： $\tau=J_{s}^{\mathrm{T}}(\theta)\mathcal{F}_{s}$

独立于框架的选择，我们可以简单地写

$\tau=J^{\mathrm{T}}(\theta)\mathcal{F}.\quad(5.26)$

当机器人与关节值θ处于平衡状态时，如果将外部wrench −F应用于末端执行器，则方程（5.26）计算产生反向wrench F所需的关节扭矩τ，从而使机器人保持平衡。例如，这在机器人的力控制中很重要。

还可以提出相反的问题，即由一组给定的关节力矩产生的末端执行器wrench 是什么。如果 JT 是一个 6 × 6 可逆矩阵，那么显然 $\mathcal{F}=J^{-T}(\theta)\tau$ 。如果关节的个数n不等于6，那么JT就不是可逆的，这个问题就没有很好地提出。如果机器人是冗余的(n > 6)，那么，即使末端执行器嵌入混凝土中，机器人也不会固定，关节扭矩可能会引起链接的内部运动。静力平衡假设不再被满足，我们需要包括动力学来知道机器人将会发生什么。

如果n≤6且JT∈Rn×6具有秩n，则将末端执行器嵌入混凝土中将使机器人固定。如果n<6，无论我们选择什么τ，机器人都不能在JT的零空间定义的6−n扳手方向上主动产生力，

$\mathrm{Null}(J^\mathrm{T}(\theta))=\{\mathcal{F}\mid J^\mathrm{T}(\theta)\mathcal{F}=0\},$ 因为没有致动器在这些方向上动作。然而，机器人可以在零空间（JT（θ））中抵抗任意外部施加的扳手而不移动，因为缺乏允许这些力产生运动的关节。

5.3 Singularity Analysis

Jacobian使我们能够识别机器人末端执行器失去在一个或多个方向上瞬间移动能力的姿势。这种姿态被称为运动学奇点 kinematic singularity ，或者简称为奇点。

在数学上，奇异姿态是雅可比阶J（θ）不具有最大秩的姿态。为了理解为什么，考虑体雅可比Jb（θ），其列表示为 $J_{bi},i=1,\ldots,n.$ .那么

因此，末端框架可以实现作为 $J_{bi}$ 的线性组合的扭曲。只要n≥6，Jb（θ）可以达到的最大秩为6。奇异姿势对应于Jb（θ）的秩下降到最大可能值以下的θ值；在这种姿势下，末端框架失去了在一个或多个维度上产生瞬时空间速度的能力。在奇点处丧失机动性伴随着抵抗与丧失机动性相对应方向的任意扭动的能力。

运动奇点的数学定义与物体或空间雅可比矩阵的选择无关。要知道为什么，回想一下Js(θ)和Jb(θ)之间的关系

$J_{s}(\theta)=\mathrm{Ad}_{T_{sb}}\left(J_{b}(\theta)\right)=[\mathrm{Ad}_{T_{sb}}]J_{b}(\theta)$ 或者更明确地

$J_s(\theta)=\left[\begin{array}{cc}R_{sb}&0\\\left[p_{sb}\right]R_{sb}&R_{sb}\end{array}\right]J_b(\theta).$

我们现在声称矩阵[AdTsb]总是可逆的。这可以通过检查线性方程来确定

$\left[\begin{array}{cc}R_{sb}&0\\\left[p_{sb}\right]R_{sb}&R_{sb}\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]=0.$

它的唯一解是x=y=0，这意味着矩阵[AdTsb]是可逆的。由于任何矩阵乘以可逆矩阵都不会改变其秩，因此如下

$\operatorname{rank}J_s(\theta)=\operatorname{rank}J_b(\theta),$

空间和物体雅可比矩阵的奇异点是相同的。

运动奇异性也与固定框架和末端执行器框架的选择无关。选择不同的固定框架相当于简单地重新定位机械臂，这对特定姿势是否奇异绝对没有影响。这一明显事实可以通过参考图5.10（a）来验证。相对于原始固定框架的正向运动学表示为T（θ），而相对于重新定位的固定框架的正运动学表示为T'（θ）=PT（θ）其中P∈SE（3）是常数。然后从（T′）−1̇T′得到了T′（θ）的体雅可比，记为J′b（θ）。一个简单的计算表明

$(T')^{-1}\dot{T'}=(T^{-1}P^{-1})(P\dot{T})=T^{-1}\dot{T},$

即J 'b (θ) = Jb(θ)，所以原机械臂和重新安置的机械臂的奇异点是相同的。

为了说明奇点与末端执行器坐标系无关，参考图5.10(b)，假设原末端执行器架的正运动学为T (θ)，而重新定位后的末端执行器架的正运动学为T ' (θ) = T (θ)Q，其中Q∈SE(3)为常数。这一次，看看空间雅可比矩阵回想一下Jb(θ)的奇异点与Js(θ)的奇异点重合，让J'(θ)表示T ' (θ)的空间雅可比矩阵。一个简单的计算就揭示了这一点

$\dot{T}'(T')^{-1}=(\dot{T}Q)(Q^{-1}T^{-1})=\dot{T}T^{-1}.$

也就是说，J 's (θ) = Js(θ)，使得运动奇异点对于末端执行器坐标系的选择是不变的。

在本节的剩余部分中，我们将考虑在具有转动关节和移动关节的六自由度开链中出现的一些常见的运动学奇点。现在我们知道空间雅可比矩阵和物体雅可比矩阵都可以用于我们的分析;我们在下面的例子中使用空间雅可比矩阵。

Case I: Two Collinear Revolute Joint Axes

我们考虑的第一种情况是两个旋转关节轴共线（见图5.11（a））。在不失一般性的情况下，这些关节轴可以标记为1和2。Jacobian的相应列为

$J_{s1}(\theta)=\left[\begin{array}{c}\omega_{s1}\\-\omega_{s1}\times q_{1}\end{array}\right]\quad\text{ and }\quad J_{s2}(\theta)=\left[\begin{array}{c}\omega_{s2}\\-\omega_{s2}\times q_{2}\end{array}\right].$

由于两个关节轴共线，我们必须具有ωs1=±ωs2；设正号， $\omega_{si}\times(q_1-q_2)=0\text{ for }i=1,2.$ 那么Js1＝Js2，集合{Js1，Js2，…，Js6}不能线性独立，并且Js（θ）的秩必须小于6。

Case II: Three Coplanar and Parallel Revolute Joint Axes 案例二：三个共面平行旋转关节轴

我们考虑的第二种情况是，三个旋转关节轴平行且位于同一平面上（三个共面轴：见图5.11（b））。在不失一般性的情况下，我们将其标记为关节轴1、2和3。在这种情况下，我们选择如图所示的固定坐标系；然后

$J_s(\theta)=\left[\begin{array}{cccc}\omega_{s1}&\omega_{s1}&\omega_{s1}&\cdots\\0&-\omega_{s1}\times q_2&-\omega_{s1}\times q_3&\cdots\end{array}\right].$

由于q2和q3是同一单位轴上的点，因此不难验证前三列不能线性独立。

Case III: Four Revolute Joint Axes Intersecting at a Common Point 四个旋转关节轴在一个公共点相交

在这里，我们考虑四个旋转关节轴在一个公共点相交的情况（图5.12）。同样，在不失一般性的情况下，将这些轴标记为从1到4。

在这种情况下，我们选择固定帧原点作为交点的公共点，使q1 =···= q4 = 0，因此

$\left.J_s(\theta)=\left[\begin{array}{ccccc}\omega_{s1}&\omega_{s2}&\omega_{s3}&\omega_{s4}&\cdots\\0&0&0&0&\cdots\end{array}\right.\right].$

前四列显然不能线性独立；一个可以写成其他三个的线性组合。例如，当肘型机械臂的手腕中心直接位于肩膀上方时，就会出现这种奇异性。

Case IV: Four Coplanar Revolute Joints 案例四：四个共面旋转关节

这里我们考虑四个旋转关节轴共面的情况。同样，在不失一般性的情况下，将这些轴标记为从1到4。选择一个固定框架，使关节轴都位于x–y平面上；在这种情况下，关节轴i方向上的单位向量ωsi∈R3的形式为

$\left.\omega_{si}=\left[\begin{array}{c}\omega_{six}\\\omega_{siy}\\0\end{array}\right.\right].$ 、

类似地，位于关节轴i上的任何参考点qi∈R3的形式

$\left.q_i=\left[\begin{array}{c}q_{ix}\\q_{iy}\\0\end{array}\right.\right],$ 以及随后 $\left.v_{si}=-\omega_{si}\times q_i=\left[\begin{array}{c}0\\0\\\omega_{siy}q_{ix}-\omega_{six}q_{iy}\end{array}\right.\right].$

空间Jacobian Js（θ）的前四列是

$\begin{bmatrix}\omega_{s1x}&\omega_{s2x}&\omega_{s3x}&\omega_{s4x}\\\omega_{s1y}&\omega_{s2y}&\omega_{s3y}&\omega_{s4y}\\0&0&0&0\\0&0&0&0\\0&0&0&0\\\omega_{s1y}q_{1x}-\omega_{s1x}q_{1y}&\omega_{s2y}q_{2x}-\omega_{s2x}q_{2y}&\omega_{s3y}q_{3x}-\omega_{s3x}q_{3y}&\omega_{s4y}q_{4x}-\omega_{s4x}q_{4y}\end{bmatrix}$

并且不能线性独立，因为它们只有三个非零分量。

Case V: Six Revolute Joints Intersecting a Common Line 案例五：六个旋转关节与一条公共线相交

我们考虑的最后一种情况是六个旋转关节轴与一条公共线相交。选择一个固定的框架，使公共线沿着z轴，并选择该公共线与关节轴i之间的交点作为轴i的参考点qi∈R3；因此，每个qi的形式为qi＝（0，0，qiz），并且

这显然是奇异的。

5.4 Manipulability

在上一节中，我们看到，在运动学奇点处，机器人的内效应器失去了在一个或多个方向上平移或旋转的能力。运动奇点呈现出一个二元命题——一个特定的构型要么是运动奇异的，要么不是——我们有理由问一个非奇异的构型是否“接近”奇异。事实上，人们甚至可以确定末端执行器的移动能力减弱的方向，以及减弱到什么程度。可操控性椭球允许从几何上可视化末端执行器以最小的effort或最大的effort运动的方向。2R平面机械臂的可操纵性椭球体如图5.3所示。雅可比矩阵由式(5.1)给出。

对于一般的n关节开链和坐标为q∈Rm的任务空间，其中m≤n，可操纵性椭球对应于关节速率为 $\dot{\theta}$ 的末端执行器速度，满足 $\|\dot{\theta}\|=1$ ，n维关节速度空间中的单位球面。假设J是可逆的，单位关节速度条件可以写成

如果J是满秩（即秩为m），则矩阵 $A=JJ^{\mathrm{T}}\in\mathbb{R}^{m\times m}$ 是方阵、对称的和正定的，如 $A^{-1}$ 。查阅线性代数教科书，我们发现对于任何对称正定 $A^{-1}\in\mathbb{R}^{m\times m}$ ，向量集 ${\dot{q}}\in\mathbb{R}^{m}$ 满足

$\dot{q}^\mathrm{T}A^{-1}\dot{q}=1$ 定义m维空间中的椭球体。设vi和λi为A的特征向量和特征值，椭球主轴方向为vi，主半轴长度为 $\sqrt{\lambda_{i}},$ ，如图5.13所示。此外，椭球体的体积V与半轴长度的乘积成比例：

对于几何Jacobian J（末端效应器框架中的Jb或固定框架中的Js），我们可以将6×n Jacobian表示为 $\left.J(\theta)=\left[\begin{array}{c}J_\omega(\theta)\\J_v(\theta)\end{array}\right.\right],$ 其中Jω包括J的顶部三行，Jv包括J的底部三行。将两者分开是有意义的，因为角速度和线速度的单位不同。这导致了两个三维可操纵性椭球，一个用于角速度，另一个用于线速度。这些可操纵性椭球具有与特征向量A对齐的主半轴，其长度由特征值的平方根给出，其中角速度可操纵性椭圆体为 $A=J_{\omega}J_{\omega}^{T}$ ，线速度可操纵率椭球体为 $A=J_{v}J_{v}^{T}$ 。

在计算线速度可操纵性椭球体时，通常使用体雅可比Jb而不是空间雅可比Js，因为我们通常感兴趣的是末端执行器框架原点处的点的线速度，而不是固定空间框架原点处点的线速度。

除了可操纵性椭球的几何结构外，指定一个标量测量值来定义机器人在给定姿势下移动的容易程度也是有用的。一个度量是可操纵性椭球的最长半轴和最短半轴的比率：

$\mu_1(A)=\frac{\sqrt{\lambda_{\max}(A)}}{\sqrt{\lambda_{\min}(A)}}=\sqrt{\frac{\lambda_{\max}(A)}{\lambda_{\min}(A)}}\geq1,$ 其中A＝JJT。

当μ1（A）较低（即接近1）时，可操纵性椭球几乎是球形或各向同性 isotropic 的，这意味着向任何方向移动都同样容易。这种情况通常是可取的。然而，当机器人接近奇点时，μ1（a）会变为无穷大。类似的度量μ2（A）只是μ1（A）的平方，称为矩阵A＝JJT的条件数 condition number ， $\mu_2(A)=\frac{\lambda_{\max}(A)}{\lambda_{\min}(A)}\geq1.$

同样，较小的值（接近1）是优选的。矩阵的条件数通常用于表征将该矩阵乘以向量的结果对向量中的小误差的敏感性。

最后一个度量是简单地与可操纵性椭球体的体积成正比：

$\mu_3(A)=\sqrt{\lambda_1\lambda_2\cdots}=\sqrt{\det(A)}.$ 在这种情况下，与前两个度量不同，值越大越好。

正如可操纵性椭球一样，对于满足‖τ‖=1的关节力矩τ，可以绘制力椭球。从 $\tau=J^{\mathrm{T}}(\theta)\mathcal{F}$ 开始，我们得到了与上面类似的结果，只是现在椭球满足

$1=f^\mathrm{T}JJ^\mathrm{T}f=f^\mathrm{T}B^{-1}f,$

其中 $B=(JJ^{\mathrm{T}})^{-1}=A^{-1}$ 。定义力椭球形状的是B的特征向量和特征值的平方根。

由于任何可逆矩阵A的特征向量也是 $B=A^{-1}$ 的特征向量，因此力椭球的主轴与可操纵性椭球的主轴对齐。此外，由于与每个主轴相关的 $B=A^{-1}$ 的特征值是A的相应特征值的倒数，因此力椭球的主半轴的长度由1/√λi给出，其中λi是A的特征值。因此，通过将操纵性椭球体沿每个主轴i拉伸因子1/λi，即可从操纵性椭球获得力椭球体。

此外，由于可操纵性椭球体的体积VA与半轴的乘积 $\sqrt{\lambda_{1}\lambda_{2}\cdots}$ 成比例，并且力椭球体的容积VB与 $1/\sqrt{\lambda_{1}\lambda_{2}\cdots}$ 成正比，因此两个体积VAVB的乘积是常数，与关节变量θ无关。

因此，定位机器人以增加可操纵性椭球体积测量μ3（A），同时减少力椭球体积测量值μ3（B）。这也解释了本章开头的观察结果，即当机器人接近奇点时，VA变为零，而VB变为无穷大。

5.5 Summary

让n链开链的正向运动学表示为以下指数形式的乘积：空间雅可比矩阵Js(θ)∈R6×n通过将关节速率向量与空间扭转Vs联系起来。Js(θ)的第i列由
- $J_{si}(\theta)=\mathrm{Ad}_{e^{(\mathcal{S}_1)\theta_1}\cdots e^{(\mathcal{S}_{i-1})\theta_{i-1}}}(\mathcal{S}_i),\text{for }i=2,\ldots,n,\mathrm{with~the~first~column~}J_{s1}=\mathcal{S}_{1}.$ 关节i的螺旋矢量 $J_{si}$ 在空间坐标系中表示，假设关节值θ是任意的而不是零
设n环开链的正运动学表示为指数积形式: $T(\theta)=Me^{|\mathcal{B}_1|\theta_1}\cdots e^{|\mathcal{B}_n|\theta_n}.$ 体雅可比矩阵Jb(θ)∈R6×n通过 ${\mathcal{V}_{b}}=J_{b}(\theta)\dot{\theta}$ 将关节速率向量 $\dot{\theta}\in\mathbb{R}^n$ 与末端执行器体扭转 body twist Vb = (ωb, Vb)联系起来。Jb(θ)的第i列由 $J_{bi}(\theta)=\operatorname{Ad}_{e^{-[\mathcal{B}_n]\theta_n\dots e^{-[\mathcal{B}_{i+1}]\theta_{i+1}}}(\mathcal{B}_i),}$ $\text{for}\ i=n-1,\ldots,1,\text{with}J_{bn}=\mathcal{B}_n.$ 关节i的螺旋矢量Jbi在body-frame坐标中表示，关节值θ假设为任意而不是零。
物体和空间雅可比矩阵关系为
考虑一个具有n个单自由度关节的空间开链，假设其处于静力平衡状态。设τ∈Rn为关节力矩和力的矢量，F∈R6为作用于末端执行器的扳手，在空间或体-架坐标系中均可。那么τ和F的关系是 $\tau=J_{b}^{\mathrm{T}}(\theta)\mathcal{F}_{b}=J_{s}^{\mathrm{T}}(\theta)\mathcal{F}_{s}.$
开链的运动学奇异构型，或者更简单地说，运动学奇异构型是雅可比阶不是最大的任何构型θ∈Rn。对于由转动关节和棱柱关节组成的六自由度空间开放链，一些常见的奇点包括（i）两个共线的转动关节轴；（ii）三个共面且平行的旋转关节轴；（iii）在公共点相交的四个转动关节轴；（iv）四个共面旋转接头；以及（v）与公共线相交的六个转动关节。
可操纵性椭球描述了机器人在不同方向上移动的容易程度。对于Jacobian J，可操作性椭球的主轴由JJT的特征向量定义，并且主半轴的相应长度是特征值的平方根。
力椭球描述了机器人在不同方向上产生力的容易程度。对于Jacobian J，力椭球的主轴由（JJT）−1的特征向量定义，并且主半轴的相应长度是特征值的平方根。
可操纵性和力椭球的度量包括最长的主半轴与最短的主轴的比率；此度量的平方；以及椭球体的体积。前两个度量值表明，如果它们很小（接近1），那么机器人就远不是奇异的。

5.7 Notes and References

PoE公式的一个关键优点是在Jacobian的推导中；Jacobian的列只是关节轴的（依赖于配置的 configuration-dependent）螺旋。由于对矩阵指数求导特别简单，我们还得到了雅可比矩阵列的Compact closed-form expressions 。

关于6R开链的奇点分析有大量的文献。除了本章介绍的三种情况外，在[122]和本章末尾的练习中还研究了其他情况，包括一些转动关节被移动关节取代的情况。开链奇点分析中使用的许多数学技术和分析方法也可用于确定并联机构的奇点，这是第7章的主题。机器人可操控性的概念首先由Yoshikawa以定量的方式提出[195]。现在有大量关于开链可操控性分析的文献，例如，[75,134]。

好悬给我拽开线

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
Chapter 5 Velocity Kinematics and Statics

在前一章中，我们看到了如何计算给定一组关节位置的机器人末端执行器框架的位置和方向。在这一章中，我们研究了从一组给定的关节位置和速度计算开链末端执行器 twist 的相关问题。在我们将末端执行器扭转表示为V∈R6之前，从5.1节开始，让我们考虑这样一种情况，即末端执行器的构型由坐标的最小集合表示，速度由给出。在这种情况下，正运动学可以写成其中θ∈Rn是关节变量的集合。根据链式法则，t时刻的时间导数是其中J(θ)∈Rm×n称为雅可比矩阵。雅可比矩阵表示末端执行器速度对关节速度的。
复制链接

扫一扫