[论文阅读] Learning Dexterous Manipulation Policies from Experience and Imitation

已于 2024-03-01 11:54:12 修改
阅读量1.9k 收藏 37
点赞数 42
文章标签： 论文阅读
于 2024-02-29 00:04:47 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_33673253/article/details/136357951
版权

时间：2016/11/15

作者相关：Vikash Kumar: Senior Research Scientist in Robotics and Embodied AI (vikashplus.github.io)

摘要

  • 基于学习的方法，用于对灵巧五指手进行非抓握操作的反馈控制
  • 学习得到能够从预定义的初始状态开始执行任务的本地控制器
  • 控制器是利用直接从传感器数据中学习到的局部线性时变模型locally-linear time-varying models 的轨迹优化 trajectory optimization 来构建的
    • 对于有一些初始条件的初始状态，可以在模拟和物理平台上稳健地执行任务
  • 还用两种插值 interpolation 方法来对更多的初始条件进行泛化：深度学习和最近邻 nearest neighbors
    • 发现最近邻可以获得更高的性能，最近邻方法基于通过运动捕捉感知的与初始对象状态的接近度，在时变的局部控制器之间切换
    • 神经网络可以只使用触觉和本体感觉反馈，而不使用关于对象的视觉反馈，并学习时不变策略
  • 我们的工作表明:
    • 基于局部轨迹的控制器可以从少量的训练数据中构建复杂的非抓握操作任务
    • 这些控制器的集合可以内插以形成更多的全局控制器

关键词

Reinforcement Learning, Dexterous Manipulation, Trajectory Optimization

Introduction
  • 不依赖于手动设计的控制器，通过优化高级成本函数，以及通过构建人类提供的专家演示来自动合成控制器
  • 学习每个控制器所需的少量数据(在物理硬件上大约60次试验)
  • 使用ADROIT平台，带有高性能气动执行器的shadowwhand骨架
    • 具有100维连续状态空间；40维连续控制空间
  • 我们的方法可以分类为基于模型的强化学习(RL)或自适应最优控制
    • 无模型和有模型的强化学习
    • 自适应控制主要侧重于学习具有预定义结构的模型的参数，本质上是将系统识别与控制交织在一起
  • 我们的方法介于两者之间，依赖于一个模型，但该模型没有任何信息预定义的结构，是从数据中学习的时变线性模型，使用通用先验进行正则化
    • 将先前研究的14维状态空间拓展到这里的100维状态空间
  • 学习的操作技巧最初表示为时变线性高斯控制器
  • 通过遥操作演示来初始化控制器来学习更复杂的操作技能
  • 通过两种方式进行泛化来适应任务的不同初始条件

Related Work

  • 机器人强化学习与灵巧手控制
  • 实验表明，我们的方法可以学习复杂精确抓取任务的策略，并可以推广到目标物体初始位置的变化
  • 通过数据手套远程操作，将从经验中学习与从人类演示中模仿学习相结合，克服了这一挑战
  • 通过演示初始化控制器是机器人强化学习中广泛使用的技术，简单的成本可能导致较差的局部最优，我们根据示例演示来定义成本

System

Hardware Platform

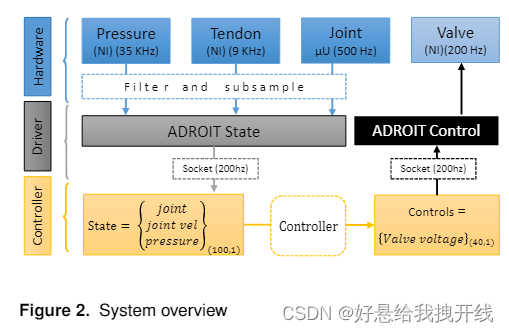
ADROIT平台，24自由度的手安装在固定的底座上，使系统仅适用于基于手指和基于手腕的操纵策略

抓握对象：装满咖啡豆的长管，每一端都装有PhaseSpace有源红外标记用于估计对象位置和速度（线速度和角速度），它们也作为状态变量提供

所有的传感器都具有相对较低的噪声，因此在将传感器数据发送到控制器之前，我们用最少的滤波

Simulation Platform

使用我们开发的MuJoCo模拟器

Reinforcement Learning with Local Linear Models

用于控制气动五指手的强化学习算法推导遵循先前的工作(Levine and Abbeel 2014)

  • 目的是学习形式为p(\mathbf{u}_t|\mathbf{x}_t)=\mathcal{N}(\mathbf{K}_t\mathbf{x}_t+\mathbf{k}_t,\mathbf{C}_t) 的时变线性高斯控制器
    • 其中xt和ut是时间步长t的状态和动作
    • 动作对应于气动阀的输入电压
  • 算法目的：最小化在轨迹 \tau=\{\mathbf{x}_{1},\mathbf{u}_{1},\ldots,\mathbf{x}_{T},\mathbf{u}_{T}\}上的期望E_{p(\tau)}[\ell(\tau)]
    • 其中\ell(\tau)=\sum_{t=1}^{T}\ell(\mathbf{x}_{t},\mathbf{u}_{t})是总成本
    • the expectation is under \begin{aligned}p(\tau)=p(\mathbf{x}_{1})\prod_{t=1}^{T}p(\mathbf{x}_{t+1}|\mathbf{x}_{t},\mathbf{u}_{t})p(\mathbf{u}_{t}|\mathbf{x}_{t}),\end{aligned}
      • 其中p(\mathbf{x}_{t+1}|\mathbf{x}_{t},\mathbf{u}_{t})是 the dynamics distribution
Optimizing Linear-Gaussian Controllers
  • 时变线性-高斯控制器结构简单，即使在未知动力学的情况下也能很好地进行优化
  • ，
  • 在机器人上运行当前控制器p(ut|xt)以收集N个样本，用这些样本拟合形式为p(\mathbf{x}_{t+1}|\mathbf{x}_t,\mathbf{u}_t)=\mathcal{N}(f_{\mathbf{x}t}\mathbf{x}_t+f_{\mathbf{u}t}\mathbf{u}_t+f_{ct},\mathbf{F}_t)的时变线性高斯动力学
    • 计算了成本函数在每个样本周围的二阶展开式并平均在一起，以获得局部近似成本函数
    • 形如
最低0.47元/天 解锁文章
【强化学习论文合集】二十九.2021国际机器学习大会论文(ICML2021)
计算机科研杂货铺
11-26 2943
强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题。
A Guide Resource for Deep Reinforcement Learning
AI拉呱，专注于人工智与网络安全方面的研究，关注一起学习。
12-24 872
A Guide Resource for Deep Reinforcement Learning 1. About this work: This deep intensive learning database was initiated by the 【 Deep Reinforcement Learning Laboratory(DeepRL-Lab) 】and was jointly c...
[论文阅读] Learning Complex Dexterous Manipulation with Deep Reinforcement Learning and Demonstrations
qq_33673253的博客
02-29 899
灵巧的多指手操作由于高维数和大量的潜在接触，有效地控制仍然具有挑战性。我们证明了无模型DRL可以有效地扩展到高维24自由度手的复杂操作任务通过使用少量的人工演示，可以显著降低样本复杂性，这使得学习的样本量相当于几个小时的机器人经验使用演示导致policy表现出非常自然的运动，和鲁棒性用行为克隆对策略进行预训练，然后用策略梯度进行微调，并增加损失以接近演示，大大降低了样本复杂性，使训练能够在相当于真实世界机器人几个小时的时间内进行。
推荐文章：DexMV —— 从人类视频中学习灵巧操作的革新之路
gitblog_00794的博客
08-26 525
推荐文章：DexMV —— 从人类视频中学习灵巧操作的革新之路 项目地址:https://gitcode.com/gh_mirrors/de/dexmv-sim 项目介绍 在机器人领域，模仿学习正逐渐成为连接人工智能与现实世界的桥梁。今天，我们要向大家推荐一个前沿的开源项目——DexMV（Dexterous Manipulation from Human Videos）。由Yuzhe Qin等学...
【强化学习与机器人控制论文 2】基于强化学习的五指灵巧手操作
Echooo的博客
11-01 2715
基于强化学习的五指灵巧手操作1. 引言2. 论文解读2.1 背景2.2 论文中所用到的强化学习方法2.3 实验任务和系统2.4 仿真到实物的迁移2.5 分布式RL训练——从状态中学到控制策略2.6 ResNet——从视觉中得到状态估计2.7 实验结果3. 总结 1. 引言 本文介绍一篇OpenAI团队出品，2018年挂在arXiv上，2020年被机器人领域顶刊 The International Journal of Robotics Research 接收的文章：Learning dexterous in
向人类学习如何抓取：数据驱动的架构 拟人软手自主抓握
10-20
软手是将顺应性元素嵌入其机械设计中的机器人系统。这样可以有效地适应物品和环境，并最终提高其抓握性能。如果与经典的刚性手相比，这些手在人性化操作方面具有明显的优势，即易于使用和坚固耐用。但是，由于缺乏合适的控制策略，它们在自主控制方面的潜力仍未得到开发。为了解决这个问题，在这项工作中，我们提出了一种方法，可以从观察人类策略开始，使软手能够自主地抓握物体。通过深度神经网络实现的分类器将要抓取的物体的视觉信息作为输入，并预测人类将执行哪些操作来实现目标。因此，此信息用于从一组人类启发的原语中选择一个，这些原语将软手姿势的演变定义为预期动作和基于触摸的反应性抓握的组合。该体系结构的硬件组件包括用于观察场景的RGB摄像头，7自由度操纵器和柔性手。柔性手在指甲处装有IMU，用于检测与物体的接触。我们使用20个对象对提出的体系结构进行了广泛的测试，在111个抓取过程中，成功率为81.1％。
如何去实现机械灵巧手玩魔方和弹钢琴_机械“影子手”上线！玩转魔方不在话下！...
weixin_39902875的博客
12-23 163
人形机器人伸出的手据国外媒体报道，人工智能研究人员让机器人来玩魔方，以此测试它的灵巧度。人类可以相对轻松地玩弄魔方，但对于机器人来说，这一直以来都非常困难。(常见的2x2x2魔方共有367.416万个内部组合。)这并不是说没有机器人能玩得转魔方——麻省理工学院的一项发明最近以破纪录的0.38秒内解出魔方——但这种机器人通常都涉及专门制造的马达和控制器。令人鼓舞的是，腾讯和香港中文大学的一组研究人员...
ALOHA论文翻译：Learning Fine-Grained Bimanual Manipulation with Low-Cost Hardware
机器学习实战
01-16 3442
斯坦福ALOHA、ACT算法
基于视觉的机器人抓取: 论文及代码(Vision-based Robotic Grasping: Papers and Codes)
热门推荐
dsoftware的博客
10-22 2万+
最近总结了基于视觉的机器人抓取的相关论文及代码，同步于github。根据抓取的类别，基于视觉的机器人抓取可以分为两类：2D平面抓取以及6D空间抓取。这个页面总结了近年来涉及到的各种各样的方法，其中大部分都使用了深度学习。总结的中文框架结构如下： 0.综述论文 1. 2D平面抓取 这类方法将抓取，用平面内旋转的矩形框表示； 1.1基于RGB或者RGB-D的方法 采用基于目标检测类的方法，直接得到2D...
开源Tacchi 视触觉传感器仿真器，为机器人与物体接触仿真提供高质量的Sim2Real性能！
weixin_44887311的博客
11-21 889
3）触觉图像生成Tacchi提供了基于表面形变生成触觉图像的功能：深度图生成：使用2D插值方法，将离散粒子的表面形变信息转化为连续的深度图。5、运行指南1）STL/PLY/PCD格式转换（0_stl2npy）此模块提供了将几何文件转换为Numpy格式的工具，便于加载并用于仿真：STL转PLY：stl2ply.pyPLY转PCD：ply2pcd.pyPCD转Numpy：pcd2npy.py注意：obj_1、obj_10和obj_100子目录包含预先转换的.npy文件，表示不同粒子密度下的几何对象模型。
深度强化学习mujoco平台搭建指南
08-21
详细总结了如何在ubuntu16.04的基础上搭建深度强化学习mujoco的环境，可按照Openai的gym针对mujoco-py进行深度强化学习训练，解决了mujoco安装后，Ubuntu重启键盘鼠标失灵的情况。
Adroit:ShadowHand ADROIT MuJoCo模型
05-28
熟练操作平台 Adroit操纵平台是由在此博士期间设计和开发的可重构，由腱驱动的气动平台。 （）研究动态灵巧操纵。 Adroit由骨架（由开发）和定制手臂组成，并由定制的致动系统提供动力。 这种定制的致动系统使Adroit能够比人手更快地移动ShadowHand骨骼（极限运动70毫秒，总反射潜伏期30毫秒），产生足够的力（每个手指腱40 N，每个腕腱125 N） ，并在机械水平上达到很高的顺应性（系统通电时指尖会产生6克的外力使手指移位。）这种速度，力和顺应性的结合是灵巧操纵的先决条件，但从未有过用肌腱驱动的系统实现，更不用说具有24个自由度和40个肌腱的系统了。 Mujoco模型 Adroit是28自由度系统，由24自由度ShadowHand和4自由度臂组成。 该存储库包含系统开发过程中的Mujoco模型，这些模型要格外小心并非常注意细节。 在项目中 Adroit已用于各种各样的项目中。
论文阅读笔记 [IEEE RAL] Tacchi: A Pluggable and Low Computational Cost Elastomer Deformation Simulator for
weixin_45693821的博客
02-13 455
论文阅读笔记 [IEEE RAL] Tacchi: A Pluggable and Low Computational Cost Elastomer Deformation Simulator for Optical Tactile Sensors 基于弹性体形变仿真的视触觉传感器仿真器 视触觉传感器是机器人研究的一个新型方向，这类传感器利用视觉图像作为传感信息提供触觉感知。 视触觉传感器的仿真主要利用光学仿真或基于数据驱动方法的图像处理，这些方法没有对传感器的弹性形变进行仿真，物理意义不强或效果不够好；
Mujoco基本情况介绍
逐日者
02-10 9989
基本情况 Mujoco是一个跨平台的机器人建模软件。 官方的介绍是这样的： MuJoCo is a physics engine that aims to facilitate research and development in robotics, biomechanics, graphics and animation, and other areas where fast and accurate simulation is needed. 不同于webots的1G多的大小，Mujoco windo
【强化学习纲要】8 模仿学习
qq_43058281的博客
03-13 3059
【强化学习纲要】8 模仿学习8.1 模仿学习概要8.2 Behavioral cloning and DAGGER8.3 Inverse RL and GAIL8.4 进一步改进模仿学习的模型8.5 模仿学习和强化学习结合8.6 Case studies 周博磊《强化学习纲要》 学习笔记 课程资料参见：https://github.com/zhoubolei/introRL. 教材：Sutton and Barton 《Reinforcement Learning: An Introduction》 8.1
【论文阅读】基于客户端数据子空间主角度的聚类联邦学习分布相似性高效识别
wzx_442011334的博客
05-09 869
PACFL的一个理想特性是它能够处理客户的部分参与。PACFL并不要求事先知道某些客户是否可以参与该联邦，客户端可以突然加入或离开网络。如果没有指定固定的聚类数，PACFL可以形成拟合的聚数。然而，在IFCA（Ghosh等人，2020）中，聚类数必须事先确定。PACFL可以在联邦之前为用客户端进行一次性客户端聚类，而不需要关于某些客户端的可用性和数量的先前信息。相反，IFCA通过在聚类识别估计和损失函数最小化之间替进行迭代构建聚类，这在通信上成本较高。
[论文笔记] 超详细解读DeepSeek v3全论文技术报告
心宝的博客
05-08 327
（可以理解为有多个专家，但每个token只会选择一部分专家进行推理，所以一个token的预测，只会用到37B参数），DeepSeek-V3 使用了。来实现高效的流水线并行（减少空泡情况，计算和通信同时进行，提升每张显卡的利用率）。对DeepSeek-V3进行了两阶段的上下文长度扩展。，在不使用采样loss帮助下，让每个专家访问次数接近）的。2、在第二阶段，进一步扩展到128K。阶段，以使其与人类偏好保持一致，并进一步释放其潜力。个不同的高质量token训练，然后进行监督微调和。，MoE）语言模型，总共。
【多模态】IMAGEBIND论文阅读
胡侃有料的博客
05-11 899
IMAGEBIND 多模态论文梗概IMAGEBIND是一种夸模态的神经网络，以图片为中心，联合六中模态的网络（图片、文字、音频、深度图、热力图、惯性测量单元）
多模态论文笔记——Coca
最新发布
haopinglianlian的博客
05-12 547
本文详细介绍多模态模型Coca，在DALL·E 3中使用其作为captioner基准模型的原因和优势。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值