关于pytorch中scatter_add_函数的分析、理解与实现

关于scatter_add_函数的分析、理解与实现

一、 pytorch中的定义和实现原理

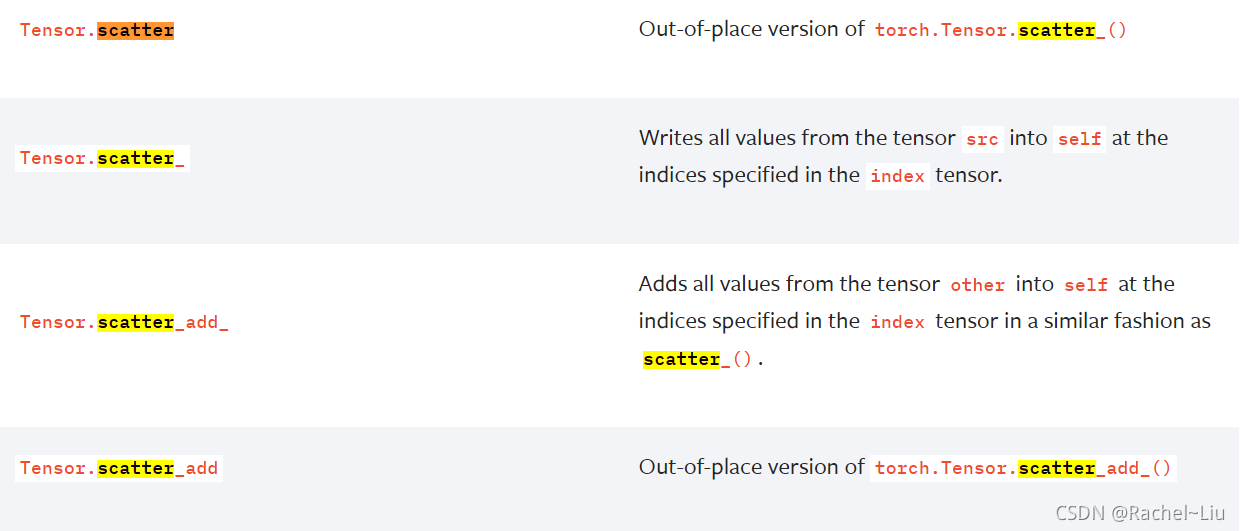
在torch._C._TensorBase.py中，定义了scatter_(self, dim, index, src, reduce=None) -> Tensor方法，作用是将src的值写入index指定的self相关位置中。用一个三维张量举例如下，将src在坐标(i,j,k)下的所有值，写入self的相应位置，而self的位置坐标除了dim维度用index[i,j,k]代替以外，都不变：

self[index[i][j][k]][j][k] = src[i][j][k]  # if dim == 0，用index[i][j][k]替换i坐标
self[i][index[i][j][k]][k] = src[i][j][k]  # if dim == 1，用index[i][j][k]替换j坐标
self[i][j][index[i][j][k]] = src[i][j][k]  # if dim == 2，用index[i][j][k]替换k坐标

要求：

• self，index，src必须有相同的维数；
• index在任意维度的size必须小于等于self和src对应维度的size
• self和index中元素的类型必须一致，dtype

>>> x = torch.rand(2, 5)
>>> x
tensor([[ 0.3992,  0.2908,  0.9044,  0.4850,  0.6004],
        [ 0.5735,  0.9006,  0.6797,  0.4152,  0.1732]])
>>> torch.zeros(3, 5).scatter_(0, torch.tensor([[0, 1, 2, 0, 0], [2, 0, 0, 1, 2]]), x)
tensor([[ 0.3992,  0.9006,  0.6797,  0.4850,  0.6004],
        [ 0.0000,  0.2908,  0.0000,  0.4152,  0.0000],
        [ 0.5735,  0.0000,  0.9044,  0.0000,  0.1732]])
"""
理解一下：
	self是一个shape为(3,5)的全零tensor；
	index是一个shape为(2,5)的tensor;
	x同index的shape相同，不相同也可。
	dim=0，意味着index需要修改第0维坐标；
	原始坐标为：00,01,02,03,04;10,11,12,13,14
	更新的横坐标依次为：01200;20012
	更新的纵坐标依次为：01234;01234
	对应组合，更新坐标为：00,11,22,03,04;20,01,02,13,24
	然后用x在原始坐标下的值填写到self更新后的坐标位置，将原始坐标和更新坐标对应来看。
	具体来看：
	x new_self
	00 00
	01 11
	02 22 
	03 03
	04 04
	10 20
	11 01
	12 02
	13 10
	14 24
"""

图示上述例子：

>>> z = torch.zeros(2, 4).scatter_(1, torch.tensor([[2], [3]]), 1.23)
>>> z
tensor([[ 0.0000,  0.0000,  1.2300,  0.0000],
        [ 0.0000,  0.0000,  0.0000,  1.2300]])
"""
理解一下：一个2*1的index_tensor（一个2维张量，两个维度的size分别是2和1，对应两个值为2和3）,dim=1,需要修改的就是1维。

原来的坐标是00,10;修改后的坐标是02,13。

然后用目标值1.23去替换self中坐标02,13的值，得到上述结果。
"""
>>> z = torch.ones(2, 4).scatter_(1, torch.tensor([[2], [3]]), 1.23, reduce='multiply')
>>> z
tensor([[1.0000, 1.0000, 1.2300, 1.0000],
        [1.0000, 1.0000, 1.0000, 1.2300]])
"""
同上：用目标值找到self在更新坐标位置的值，乘以目标值1.23得到更新后的矩阵。
"""

类似于上述方法，在python中还包括scatter_add(dim, index, src) -> Tensor用于实现将src按照index位置累加到self上。

python实现scatter_add_方法

分为以下几个步骤：

1. 获得坐标：将index所有的坐标按照从上到下，从左到右的顺序存储到数组raw_index中；

   此处我的思路是逐个获取每一位坐标值，再拼接起来，具体如下：获取index的shape和维数，从最高维度开始记录，计算每一维度的坐标值需要重复出现的次数（从0到该维度的shape-1重复的次数）。如shape=(2,2,1)，先看最高维的2，可以得到[[][][0][0][1][1]]，然后往列表中添加下一维的2，可以得到[[][][0,0][0,1][1,0][1,1]]，最后处理最后一维，可以得到[[][][0,0,0][0,1,0][1,0,0][1,1,0]]。这个思路避免了不确定维数的tensor多层循环shape的复杂。具体代码实现如下，计算需要出现的次数得到一个坐标矩阵，需要转置才能得到理想状态。

2. 转换坐标：按照dim和index修改原始坐标，得到新的坐标index_pos；

3. 累加值：self_tensor在index_pos位置的值要累加上other_tensor在raw_index位置的值

import torch
import numpy as np
from torch import Tensor
"""
@overload
def scatter_add(self, dim: _int, index: Tensor, src: Tensor) -> Tensor: ...
@overload
def scatter_add(self, dim: Union[str, ellipsis, None], index: Tensor, src: Tensor) -> Tensor: ...
def scatter_add_(self, dim: _int, index: Tensor, src: Tensor) -> Tensor: ...

对pytorch中的scatter_add函数的理解和简单测试：
# 参数：tensor,dim,index,tensor
# 返回：tensor
# 功能：将other_tensor的值累加到self_tensor的相应位置，用index_tensor对应位置的值替换掉self_tensor下标的dim维
# 举例：
    self_tensor  = [[1, 2], [3, 4]] shape=(2,2)
    other_tensor = [[5, 6], [7, 8]] shape=(2,2)
    index_tensor = [[0, 0], [1, 1]] shape=(2,2)
    dim = 1
    以上三个tensor的shape必须一致，下标为：[0,0] [0,1] [1,0] [1,1]
    dim=1，那么，self_tensor的第1维下标由index_tensor表示，[0,0] [0,0] [1,1] [1,1]
    则:
        self_tensor[0,0] = 1 + 5 + 6 = 12
        self_tensor[0,1] = 2
        self_tensor[1,0] = 3
        self_tensor[1,1] = 4 + 7 + 8 = 19
"""
def scatter_add(input_tensor: torch.Tensor, dim: int, index: torch., other: torch.Tensor) -> torch.Tensor:
    # tensor的维数是不确定的，因此无法用for循环的方式
    # 如果tensor是2维，那么dim=0或1，两层for循环，用other对self进行填充
    # 如果tensor是3维，那么dim=0、1、2，需要三层for循环来遍历other
    if input_tensor.dim() == 2:
        for i in range(index_tensor.size()[0]):
            for