Qiskit 学习笔记1

溴锑锑跃迁

已于 2022-04-25 08:14:31 修改

阅读量5.2k

点赞数 22

分类专栏： Qiskit学习文章标签： python 量子力学

于 2021-01-11 22:18:08 首次发布

本文链接：https://blog.csdn.net/qq_33943772/article/details/112407019

版权

Qiskit学习专栏收录该内容

12 篇文章 68 订阅

订阅专栏

预备工作：安装与简单测试

运行环境：Win10(64bits) + Anaconda 3 + Visual Studio Code（以下简称vscode）

用pip安装qiskit库（建议顺便安装 pylatexenc ,否则后期会出现某些错误）：命令行下输入pip install qiskit，如果条件允许可以考虑科学上网，否则会白浪费很多时间（前:4KB/s，后:700KB/s）
在vscode的插件市场里搜索qiskit（建议官方的相关插件都安装上）

Qiskit官方网站：Qiskit，学习资源和社区氛围都很不错

from qiskit import * #非必需，只是为了方便
circ = QuantumCircuit(3) #创建一个有三个量子比特的量子电路
circ.h(0)    #给第0个比特加一个H门
circ.cx(0, 1)    #给第0和1个比特加一个Cx门
circ.cx(0, 2)

#选择一个用于执行的后端，此处即态矢后端
backend = Aer.get_backend('statevector_simulator')
job = execute(circ, backend)    #execute()专门用于执行电路
result = job.result()

output = result.get_statevector(circ, decimals=3)
print(output)

其中的H门相当于创建一个 $\left|\0\right\rangle$ 和 $\left|\1\right\rangle$ 的叠加态，概率各为 $\frac{1}{2}$ ，而其中的Cx门（控制非门）本来有它自己的矩阵表述，这里可以暂且理解为根据第一个提供的量子比特（参考比特）决定是否反转第二个量子比特（被操作比特），比如说qubit_0处于0的量子态（state）时，就不会反转qubit_1，反之亦然

由上操作我们可以得到000或111的量子态

整体流程可以简化为：导入Qiskit库 → 编辑电路（进行操作如设置门）→ 选择后端并执行 → 获取结果

更多更深入了解可以参考官网的讲义或者阅读量子计算通识 - 简书中的有关部分

本篇内容参考：Circuit Tutorials — Qiskit 0.36.1 documentation

初识：后端

后端由Aer库提供

参考：Getting Started with Qiskit — Qiskit 0.36.1 documentation

酉后端（Unitary backend）：

Qiskit Aer also includes a unitary_simulator that works provided all the elements in the circuit are unitary operations. This backend calculates the $2^n \times 2^n$ matrix representing the gates in the quantum circuit.

当你用矢量的思想去思考量子态时，酉后端实际上就是计算当前电路的等效矩阵（本质上是计算每一个矩阵元）

# 默认已导入Aer库
# 由Aer库获取酉后端
backend = Aer.get_backend('unitary_simulator')
#---------------codes----------------#
# 获取结果
result.get_unitary(circ, decimals=3)

OpenQASM后端:

对一个量子电路，我们需要测量它来得到（理想的）实际结果，否则我们不能从量子态中得到任何信息。而测量这一行为则会导致量子比特坍缩到经典比特。

# 可以接续我们的测试代码
# 再创建一个量子电路以进行测量操作
# 绘图时会生成3 qubits + 3 bits = 6个道
meas = QuantumCircuit(3, 3)
# 在第0~2个量子比特道上加一个隔板以进行区分
meas.barrier(range(3))
# 建立从量子到经典的测量映射，相当于把测量结果移至经典道
meas.measure(range(3), range(3))

# 电路的可加性
qc = circ + meas

# 绘图（可选）
# qc.draw()

绘图时会生成如下电路图（更多绘图方面的知识会往后放，进行可视化操作时出于方便的考虑，建议使用Jupyter）：

     ┌───┐           ░ ┌─┐
q_0: ┤ H ├──■────■───░─┤M├──────
     └───┘┌─┴─┐  │   ░ └╥┘┌─┐
q_1: ─────┤ X ├──┼───░──╫─┤M├───
          └───┘┌─┴─┐ ░  ║ └╥┘┌─┐
q_2: ──────────┤ X ├─░──╫──╫─┤M├
               └───┘ ░  ║  ║ └╥┘
c: 3/═══════════════════╩══╩══╩═
                        0  1  2

（现在大概可以理解之前说的Cx门、隔板、道等概念了）

如果要模拟上述电路，我们就要使用OpenQASM后端。每一次运行都会生成一个000或111的经典比特串（classical bitstring）。之所以强调经典，是因为先前在量子道中，我们理论上在操作后（一次H门，两次Cx门）得到的其实是：

$\left|\psi\right\rangle=\frac{\left|000\right\rangle+\left|111\right\rangle}{\sqrt{2}}$

（注意，对每一个独立的态，其系数平方便等于测量它时相应的概率，显而易见，对 $/\psi>$ 的测量结果只有 $/000>$ 和 $/111>$ 两种，概率各为 $\frac{1}{2}$ ，其总和为 $1=100\%$ ）

现在我们想基于大量样本通过“频率来估计概率”，所以有如下代码：

# 导入OpenQASM后端
backend2 = Aer.get_backend('qasm_simulator')

# 基于OpenQASM后端运行我们的电路
# 这里用参数shots把样本数设定为1024（然而事实上是默认值）
job = execute(qc, backend2, shots=1024)

# 获得结果
result = job.result()

counts = result.get_counts(qc)
print(counts)

结果由于是随机事件因人、机而异，但理论上应只有两种经典比特串（后期我们会讨论凭借注册的IBM Q账号使用IBM提供的量子计算机进行实际的操作，由于实际环境影响，很可能会出现一些“意料之外”的结果）

可视化

直方图（Histogram）：

plot_histogram函数头：

def plot_histogram(data, figsize=(7, 5), color=None, number_to_keep=None,
                   sort='asc', target_string=None,
                   legend=None, bar_labels=True, title=None, ax=None)

同时出于练习的目的，此处采用一个和官网不同的例子：

import numpy as np
from qiskit import QuantumCircuit
from qiskit import Aer
from qiskit import execute
from qiskit.visualization import plot_histogram #绘制直方图

circ = QuantumCircuit(3)
meas = QuantumCircuit(3, 3)
# 根据测试部分中的描述，现在第0个和第2个量子比特都处于/0>和/1>的叠加态
# 每个单态的概率皆为50%=1/2
circ.h(0)
circ.h(2)
circ.cx(0, 1)

meas.barrier(range(3))
meas.measure(range(3), range(3))
qc = circ + meas

backend = Aer.get_backend('qasm_simulator')
result1 = execute(qc, backend).result()
result2 = execute(qc, backend).result()

counts1 = result1.get_counts(qc)
counts2 = result2.get_counts(qc)
legends = ['1st', '2nd'] # 加入图例
fig = plot_histogram([counts1, counts2], legend=legends, figsize=(10, 7))
# 有单独的开发环境者可以用如下方式查看可视化结果（其实就是图片）
# jupyter玩家可以自动注释掉下面一行
fig.savefig('out.png') # 路径一定要写清楚，不要自己都找不到！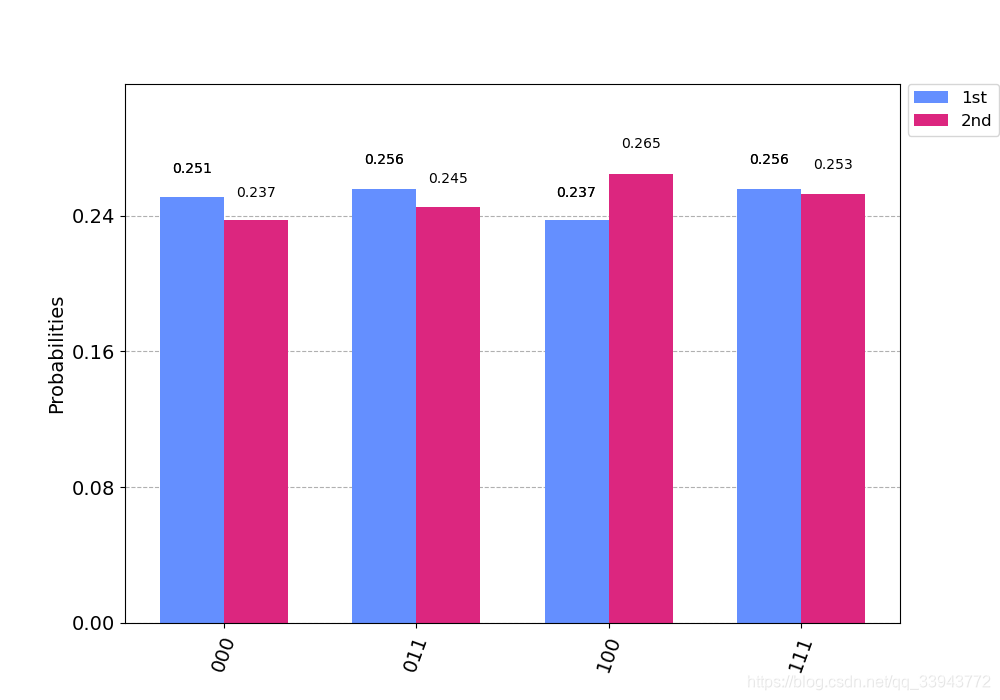

绘制直方图时可用的选项：

legend=：图例，类型为字符串列表
sort=：排序方式，可选值为'asc'或'dsc'，即升序或降序
number_to_keep：参数类型为整数，即需要分类展示的项目个数，余项合并作一组展示
color：类型为字符串或字符串列表
bar_labels：类型为布尔类型，即是否在每一个直方上打印标签
figsize：元组，即图片长宽

态的绘制：

背景知识：量子态

量子态可以是一个态矢量 $/\psi>$ 或一个态矩阵ρ：

$\rho=\left|\psi\right\rangle\left\langle\psi\right|$

更普遍地，对混合态而言：

$\rho=\sum_k \left|\psi_k\right\rangle\left\langle\psi_k\right|$

官方提供了如下函数以应对不同的绘制场景(注意，因为是态的绘制，故而需要使用态矢后端，即我们曾在测试中使用过的后端)：

plot_state_city：将量子态矩阵分成实部和虚部进行绘制，成图中态矩阵会形似城市中的高楼，下称“市图”
plot_state_qsphere：Qiskit中的特色菜，将某量子态的振幅和相位绘制在球体中，并分别用线条粗细和颜色区分.对混合态则会将每个分量的qsphere绘制出来，下称“Q球图”
plot_state_paulivec：相当于用泡利算符展开量子态
plot_state_hinton：和'city'基本相同，不同的是元素的大小表示的是矩阵元的值
plot_bloch_multivector：将量子态投影到一个qubit空间并绘制在一个bloch球上

下面按顺序给出实例代码：

import numpy as np
from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_state_city, plot_state_hinton

# 创建一个Bell态，试综合前文所学自作解释
bell = QuantumCircuit(2)
bell.h(0)
bell.cx(0, 1)

# 一定要用态矢后端！
backend = Aer.get_backend('statevector_simulator')
result = execute(bell, backend).result()

fig_city = plot_state_city(result.get_statevector(bell))
fig_hinton= plot_state_hinton(result.get_statevector(bell))

fig_city.savefig('city.png')
fig_hinton.savefig('hinton.png')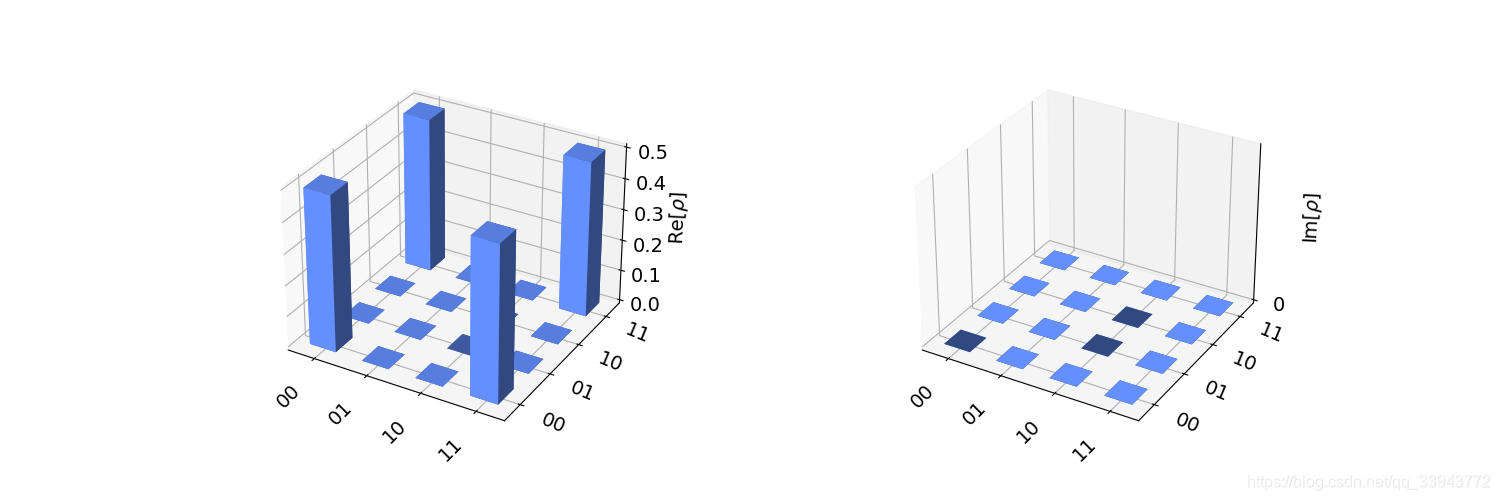

（就目前来看Hinton图无法提供更多帮助……）

要使Q球图给人更为深刻的印象，我们采用一个不同的例子：

import numpy as np
from qiskit import QuantumCircuit, Aer, execute
# 注意此处已经更换了绘制函数
from qiskit.visualization import plot_state_qsphere, plot_bloch_multivector

# 不是Bell态！
qc = QuantumCircuit(3)
qc.h(0)
qc.h(2)
qc.cx(0, 1)

backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
fig_qs = plot_state_qsphere(result.get_statevector(qc))
fig_bm = plot_bloch_multivector(result.get_statevector(qc))
fig_qs.savefig('qsphere.png')
fig_bm.savefig('bv.png')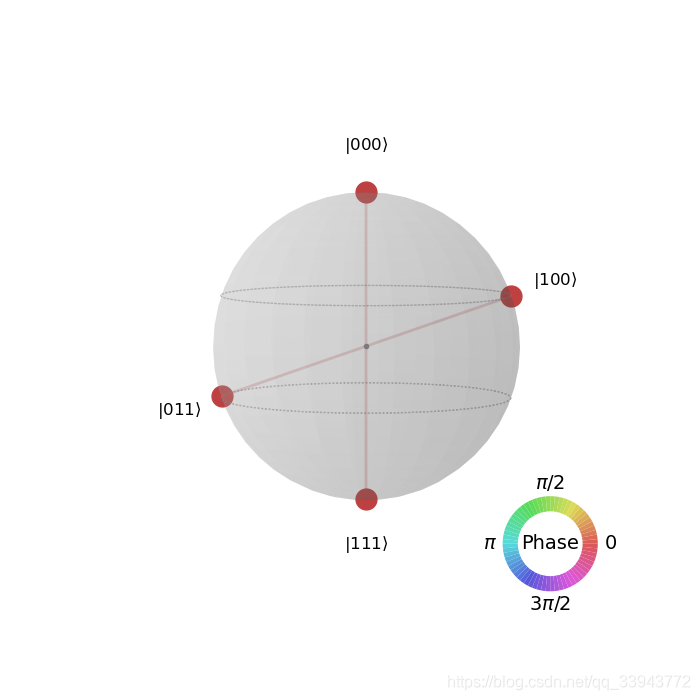

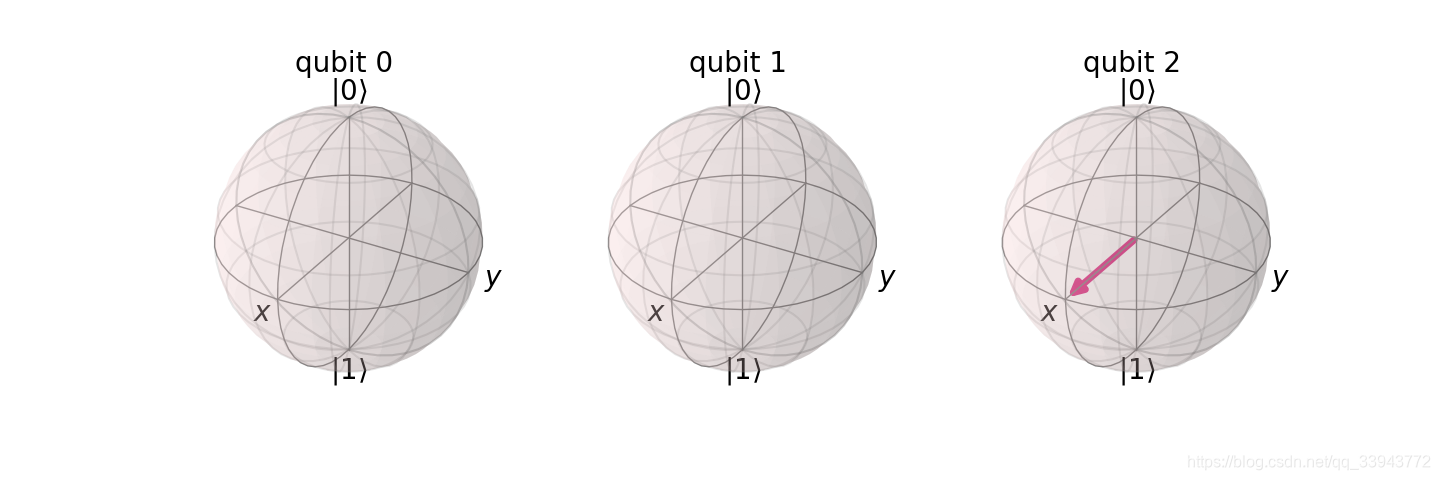
Pauli矢图只放两行关键代码吧：

from qiskit.visualization import plot_state_paulivec

fig_pv = plot_state_paulivec(result.get_statevector(qc),
        color=['pink','orange','yellow','red'])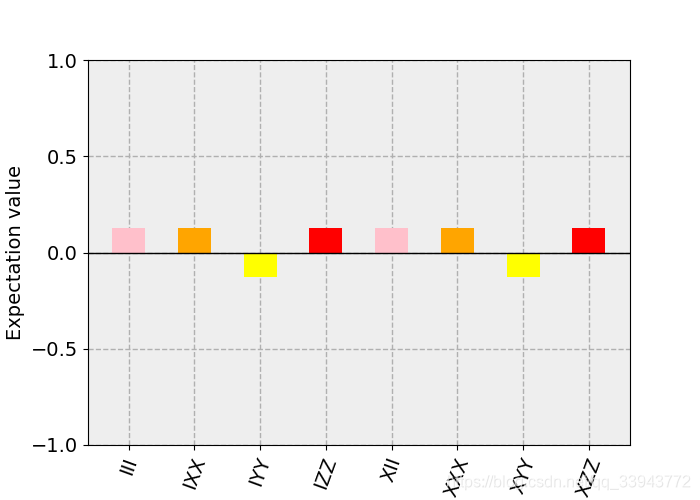

再绘制一个：Bloch矢量

Bloch矢量被定义为 $[x=Tr[X\rho],y=Tr[Y\rho],z=Tr[Z\rho]]$ ，其中ρ是态矩阵，[X，Y，Z]就是Pauli矩阵.

from qiskit.visualization import plot_bloch_vector

fig = plot_bloch_vector([0.77,-0.2,0.79])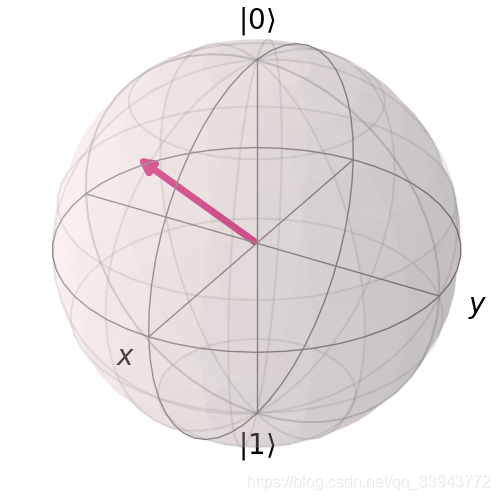

摘要：量子操作

内容提纲：

Qiskit Terra中的量子操作：单量子比特门、多量子比特门、测量、重置、条件、态初始化
三种后端的使用：酉后端、OpenQASM后端、态矢后端

预处理头：

import matplotlib.pyplot as plt
import numpy as np
from math import pi

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer

backend = BasicAer.get_backend('unitary_simulator')

单量子比特门：

背景知识：单量子比特态

任意单量子比特可写作（由于只有0和1两种状态）： $\left|\psi\right\rangle=\alpha\left|0\right\rangle+\beta\left|1\right\rangle$

或

$\left|\psi\right\rangle=\begin{pmatrix} \alpha\\ \beta \end{pmatrix}$

其中α和β为复数，但由于总概率守恒，必有 $|\alpha|^2+|\beta|^2=1$ .而又因为全局相因子是无法探测的 $\left|\psi\right\rangle := e^{i\delta} \left|\psi\right\rangle$ ，我们只需要两个实数来描述一个单量子比特态（注意我们使用 $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$ 来表示 $\left|0\right\rangle$ ， $\begin{pmatrix} 0 \\1 \end{pmatrix}$ 来表示 $\left|1\right\rangle$ ）.一种方便的表示方式是：

$\left|\psi\right\rangle=\cos\frac{\theta}{2}\left|0\right\rangle+\sin\frac{\theta}2 e^{i\phi}\left|1\right\rangle,0\leq \phi \leq 2\pi, 0 \leq \theta \leq \pi$

由上，我们就可以建立一个由 $\mathbb{C}^2$ 到 $\mathbb{R}^3$ 上一单位球面的一对一映射，这种表示方式就叫做Bloch球.

量子门（操作）通常用矩阵表示，对一个量子比特而言，门可以表示成2阶的酉矩阵U，如想让它起作用，我们只需要简单地让它通过矩阵乘法作用到一个量子态矢上： $\left|\psi'\right\rangle=U\left|\psi\right\rangle$ .

最普遍的单量子酉矩阵形式（下称广义酉矩阵）:

$U = \begin{pmatrix} \cos(\theta/2) & -e^{i\lambda}\sin(\theta/2) \\ e^{i\phi}\sin(\theta/2) & e^{i\lambda+i\phi}\cos(\theta/2) \end{pmatrix}$

除λ取值范围为[0,2π]外，其余参数取值范围不变，注意它满足 $U^{\dagger}U=I$ .它的各个矩阵元都可以经由酉后端计算出来.

q = QuantumRegister(1) # 创建一个量子寄存器

qc1 = QuantumCircuit(q)
qc1.u(pi/6,pi/2,pi/3,q) # 将普通酉矩阵中的三个参数填入
print(qc1.draw())
#       ┌────────────────┐
# q0_0: ┤ U(π/6,π/2,π/3) ├
#       └────────────────┘

# 注，如果你选择和官网一样使用u1、u2、u3，会得到警告;
# 看来官方后来是推荐使用u(θ,φ,λ)
# 另注:
#   u3(θ,ϕ,λ)=U(θ,ϕ,λ)
#   u2(ϕ,λ)=u3(π/2,ϕ,λ)
#   u1(λ)=u3(0,0,λ)
# 说有用也有道理……

job = execute(qc1, backend)
result = job.result()
print(result.get_unitary(qc1, decimals=3))
# [[ 9.65925826e-01+0.j         -1.29409523e-01-0.22414387j]
#  [ 1.58480958e-17+0.25881905j -8.36516304e-01+0.48296291j]]
# 上面的结果就是我们输入参数后的U门矩阵化表达,相当于算出了这个矩阵，或者
# 是等效了这个电路

读者可以自己推导单位矩阵的广义酉矩阵表达式.

泡利矩阵：X，Y，Z

$X=\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix},Y=\begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix},Z=\begin{pmatrix} 1 &0 \\ 0 & -1 \end{pmatrix}$

下面只给出X门的相关代码，包括其等价广义酉矩阵：

print('Output from Circuit1:')
qc1 = QuantumCircuit(q)
qc1.x(q)
print(qc1.draw())

job = execute(qc1, backend)
result = job.result()
print(result.get_unitary(qc1, decimals=3))

# Output from Circuit1:
#       ┌───┐
# q0_0: ┤ X ├
#       └───┘
# [[0.+0.0000000e+00j 1.-1.2246468e-16j]
#  [1.+0.0000000e+00j 0.+0.0000000e+00j]]

print('Output from Circuit2:')
qc2 = QuantumCircuit(q)
qc2.u(pi,0,pi,q)
print(qc2.draw())

job = execute(qc2, backend)
result = job.result()
print(result.get_unitary(qc2, decimals=3))

# Output from Circuit2:
#       ┌──────────┐
# q0_0: ┤ U(π,0,π) ├
#       └──────────┘
# [[0.+0.0000000e+00j 1.-1.2246468e-16j]
#  [1.+0.0000000e+00j 0.+0.0000000e+00j]]

官方又是这样介绍泡利矩阵的应用的：

X门：比特翻转，即 $u(\pi,0,\pi)$
Y门：比特-相位翻转，即 $u(\pi,\frac{\pi}2,\frac\pi2)$
Z门：相位翻转，即 $u(0,0,\pi)$

哈达玛德门（Hadamard gate）:

之前我们说过量子态的表达规则，经典情况下，一个比特不是0就是1，而基于前面的实践相信你也注意到了H门的不同，它可以使一个经典比特处于（事实上是最简单的）量子态：

$H=\frac{1}{\sqrt2}\begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}$

它的实例代码就不放了……

标准旋转门：

实际上就相当于复数里的SO(2)，标准旋转门被定义为绕泡利向量进行旋转操作：

$R_P(\theta) = \exp(-i \theta P/2) = \cos(\theta/2)I -i \sin(\theta/2)P$

绕X轴、Y轴、Z轴的旋转矩阵分别为：

$\\R_x(\theta) = \begin{pmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{pmatrix} = u(\theta, -\pi/2,\pi/2), \\R_y(\theta) = \begin{pmatrix} \cos(\theta/2) & - \sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2). \end{pmatrix} =u(\theta,0,0),\\ R_z(\phi) = \begin{pmatrix} e^{-i \phi/2} & 0 \\ 0 & e^{i \phi/2} \end{pmatrix}$

此处仅放Ry门实例代码：

print('Output from Circuit1:')
qc1 = QuantumCircuit(q)
qc1.ry(pi/5,q)
print(qc1.draw())

job = execute(qc1, backend)
result = job.result()
print(result.get_unitary(qc1, decimals=3))

# Output from Circuit1:
#       ┌─────────┐
# q0_0: ┤ RY(π/5) ├
#       └─────────┘
# [[ 0.95105652+0.j -0.30901699+0.j]
#  [ 0.30901699+0.j  0.95105652+0.j]]

print('Output from Circuit2:')
qc2 = QuantumCircuit(q)
qc2.u(pi/5,0,0,q)
print(qc2.draw())

job = execute(qc2, backend)
result = job.result()
print(result.get_unitary(qc2, decimals=3))

# Output from Circuit2:
#       ┌────────────┐
# q0_0: ┤ U(π/5,0,0) ├
#       └────────────┘
# [[ 0.95105652+0.j -0.30901699+0.j]
#  [ 0.30901699+0.j  0.95105652+0.j]]

单量子操作门还有Clifford门族的两个门、C3门族没有说，有足够基础的读者可以去官网进行扩展阅读.

多量子比特门：

背景知识：一点数学：这一部分可以看官方介绍，也可以浏览【科普】量子计算通识-2-四种操作与乘积态 - 简书.

额外需要提及的是：

Qiskit里乘积态的表示方法和通常的教材相反，按官方的话讲叫MSB(most significant bit)在左,LSB(less significant bit)在右，解释是便于与经典计算机中的比特串进行衔接.
在多量子比特门中，我们经常以某一个/些态作为条件来对其他态进行操作，这样的门我们称作可控门(controlled gates)

双量子比特门：

通常来说，可控双量子比特门都是根据其中一个量子比特来决定是否将一个单量子比特门施加到另一个量子比特上，对于一个单量子比特门 $U$ 和基于它生成的可控双量子比特门 $C_U$ 来说，若控制qubit 0而针对qubit 1(通常情况下是这样的，你也可以反过来，然而后面推出的表达式不尽相同)，则有：

$\begin{align*} C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle}\\ C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{U\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle}\\ C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle}\\ C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{U\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle}\\ \end{align*}$

(注意，Qiskit中比特串顺序可以理解为从右向左的，即‘⬅⬅⬅’)

要计算出完整的矩阵，我们需要如下的矩阵元计算式：

$C_{(jk), (lm)} = \left(\underset{\text{qubit}~1}{\left\langle j \right|} \otimes \underset{\text{qubit}~0}{\left\langle k \right|}\right) C_{U} \left(\underset{\text{qubit}~1}{\left| l \right\rangle} \otimes \underset{\text{qubit}~0}{\left| k \right\rangle}\right)$

有假设:

$U = \begin{pmatrix} u_{00} & u_{01} \\ u_{10} & u_{11}\end{pmatrix}$

当控制qubit 0而针对qubit 1时， $C_U = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & u_{00} & 0 & u_{01} \\ 0 & 0 & 1 & 0 \\ 0 & u_{10} &0 & u_{11} \end{pmatrix}$
反之， $C_U = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & u_{00} & u_{01} \\ 0 & 0 & u_{10} & u_{11} \end{pmatrix}$

验证：

q = QuantumRegister(2) # 创建 两 个量子寄存器！

print('Output from Circuit1:')
qc1 = QuantumCircuit(q)
qc1.cx(q[0],q[1])
print(qc1.draw())

job = execute(qc1, backend)
result = job.result()
print(result.get_unitary(qc1))

# Output from Circuit1:

# q0_0: ──■──
#       ┌─┴─┐
# q0_1: ┤ X ├
#       └───┘
# [[1.+0.j 0.+0.j 0.+0.j 0.+0.j]
#  [0.+0.j 0.+0.j 0.+0.j 1.+0.j]
#  [0.+0.j 0.+0.j 1.+0.j 0.+0.j]
#  [0.+0.j 1.+0.j 0.+0.j 0.+0.j]]

print('Output from Circuit2:')
qc2 = QuantumCircuit(q)
qc2.cx(q[1],q[0])
print(qc2.draw())

job = execute(qc2, backend)
result = job.result()
print(result.get_unitary(qc2))

# Output from Circuit2:
#       ┌───┐
# q0_0: ┤ X ├
#       └─┬─┘
# q0_1: ──■──

# [[1.+0.j 0.+0.j 0.+0.j 0.+0.j]
#  [0.+0.j 1.+0.j 0.+0.j 0.+0.j]
#  [0.+0.j 0.+0.j 0.+0.j 1.+0.j]
#  [0.+0.j 0.+0.j 1.+0.j 0.+0.j]]

官网之后的酉矩阵相关代码是100%的摘要，基本上只剩下介绍+编码用酉后端计算

非酉操作：

大部分内容都很简单而直接，比如说测量（Measurement）操作，此处酌情略过……

重置（Reset）：

重置操作允许你在计算中途将某一量子态重置到 $\left|0\right\rangle$

backend = BasicAer.get_backend('qasm_simulator') # 换用OpenQASM后端

q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.h(0)
qc.reset(q[0])
qc.measure(q,c)
print(qc.draw())

print(execute(qc,backend).result().get_counts(qc))
#       ┌───┐     ┌─┐
# q0_0: ┤ H ├─|0>─┤M├
#       └───┘     └╥┘
# c0: 1/═══════════╩═
#                  0
# {'0': 1024}

由前面所学，我们知道在施加了H门后理应是0和1概率各自近似于50%，而在重置后我们的结果是100%的0.

条件操作：

对经典道设定条件来决定是否对相应的量子道进行操作：

q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.h(0)
qc.measure(q, c)
qc.x(q[0]).c_if(c, 1)
qc.measure(q, c)
print(qc.draw())
print(execute(qc,backend).result().get_counts(qc))
#       ┌───┐┌─┐ ┌───┐ ┌─┐
# q0_0: ┤ H ├┤M├─┤ X ├─┤M├
#       └───┘└╥┘ └─┬─┘ └╥┘
#             ║ ┌──┴──┐ ║
# c0: 1/══════╩═╡ = 1 ╞═╩═
#             0 └─────┘ 0
# {'0': 1024}

第一次测量的结果应当是随机的，可结果表明只有0态，试解释其原因(分类讨论).

任意初始化（Arbitrary initialization）：

Qiskit也同样允许我们制备任意的量子态，要求很简单，总概率为100%=1.比如，现在我们想制备如下量子态：

$\left|\psi\right\rangle = \frac{i}{4}\left|000\right\rangle + \frac{1}{\sqrt{8}}\left|001\right\rangle + \frac{1+i}{4}\left|010\right\rangle + \frac{1+2i}{\sqrt{8}}\left|101\right\rangle + \frac{1}{4}\left|110\right\rangle$

代码如下：

import math
desired_vector = [
    1 / math.sqrt(16) * complex(0, 1),
    1 / math.sqrt(8) * complex(1, 0),
    1 / math.sqrt(16) * complex(1, 1),
    0,
    0,
    1 / math.sqrt(8) * complex(1, 2),
    1 / math.sqrt(16) * complex(1, 0),
    0]


q = QuantumRegister(3)

qc = QuantumCircuit(q)

qc.initialize(desired_vector, [q[0],q[1],q[2]])
print(qc.draw())

#       ┌───────────────────────────────────────────────────────────────────┐
# q0_0: ┤0                                                                  ├
#       │                                                                   │
# q0_1: ┤1 initialize(0.25j,0.35355,0.25+0.25j,0,0,0.35355+0.70711j,0.25,0) ├
#       │                                                                   │
# q0_2: ┤2                                                                  ├
#       └───────────────────────────────────────────────────────────────────┘

backend = BasicAer.get_backend('statevector_simulator')
job = execute(qc, backend)
qc_state = job.result().get_statevector(qc)
print(qc_state)
# [2.50000000e-01+0.j         0.00000000e+00-0.35355339j
#  2.50000000e-01-0.25j       0.00000000e+00+0.j
#  0.00000000e+00+0.j         7.07106781e-01-0.35355339j
#  2.77555756e-17-0.25j       0.00000000e+00+0.j        ]

真机测试：IBM Quantum Experience

这一部分是额外拓展的内容，为了我们的真机测试一切顺利，首先登陆IBM Quantum Experience并注册一个IBMid：

登陆成功后应当是如下界面：

之后在左侧选择Circuit Composer：

之后的操作就和我们平时调用draw()函数里看到的差不多了，绘制完电路后点右上角的Run on xxx执行你的电路.

具体效果因人、机而异，总之很酷！

整整码了三天，以前从没撑过摘要这一部分……

欢迎加入Qiskit交流群：498323428(误解散) 1064371332

溴锑锑跃迁

关注

22
点赞
踩
89

收藏

觉得还不错? 一键收藏
16
评论
Qiskit 学习笔记1

预备工作：安装与简单测试运行环境：Win10(64bits) + Anaconda3+ Visual Studio Code（以下简称vscode）用pip安装qiskit库（建议顺便安装 pylatexenc ,否则后期会出现某些错误）：命令行下输入pip install qiskit，如果条件允许可以考虑科学上网，否则会白浪费很多时间（前:4KB/s，后:700KB/s）在vscode的插件市场里搜索qiskit（建议官方的相关插件都安装上）Qiskit官方网站：https://qis..
复制链接

扫一扫