信号与系统 Matlab 利用DFT分析离散信号频谱

应用离散傅里叶变换(DFT)，分析离散信号x[k]。根据信号傅里叶变换建立的时域与频域之间的对应关系，可以得到有限长序列的离散傅里叶变换(DFT)与四种确定信号傅里叶变换的之间的关系，实现由DFT分析其频谱。

1. 利用FFT分析信号
   
   的频谱；

   (1) 确定DFT计算的参数；
   (2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。
   答：信号下x[k]基频，可以确定基波周期N=16，为显示k=0,1,…31，所以取N=32。

Matlab程序如下：

N=32; k=0:N-1;
x=cos(3*pi*k/8);
X=fft(x);
subplot(2,1,1);
stem(k-N/2,abs(fftshift(X)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
stem(k-N/2,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

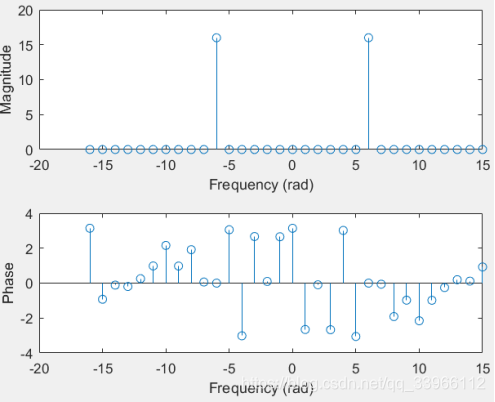
(2)由幅频特性，X[m]在m=6和-6处有值，幅度为16，可以算出基频，与理论值相符。若选取N不是16或16的整数倍，将发生频谱泄露现象。

2.利用FFT分析信号的频谱；
(1) 确定DFT计算的参数；
(2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。

答：(1)信号无限长，因此需要对其进行截短。该序列单调衰减，当k>=30时，序列已几乎衰减为0，因此只取序列在区间[0，30]上的数值进行分析。
Matlab程序如下：

k=0:30;
k1=-15:15;
x=0.5.^k;
X=fft(x);
subplot(2,1,1);
plot(k-15,abs(fftshift(X)),k1,(1+0.25-cos(k1*pi/15)).^(-0.5),'r');
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2