MATLAB中的DTFT与DFT实现及应用

本文还有配套的精品资源，点击获取

简介：DTFT是将离散时间信号转换到频率域的信号处理概念，而DFT是其在周期延拓下的离散版本，广泛用于数字信号处理。本简介探讨了在MATLAB环境下DTFT的自定义函数实现以及DFT的标准函数 fft ，并通过 testdata.mat 文件中的测试数据验证了这些函数的正确性。文章强调了DTFT与DFT的重要概念，包括DTFT公式、周期性、DFT与DTFT的关系、逆变换、傅里叶变换性质，以及在多个信号处理领域的应用实例。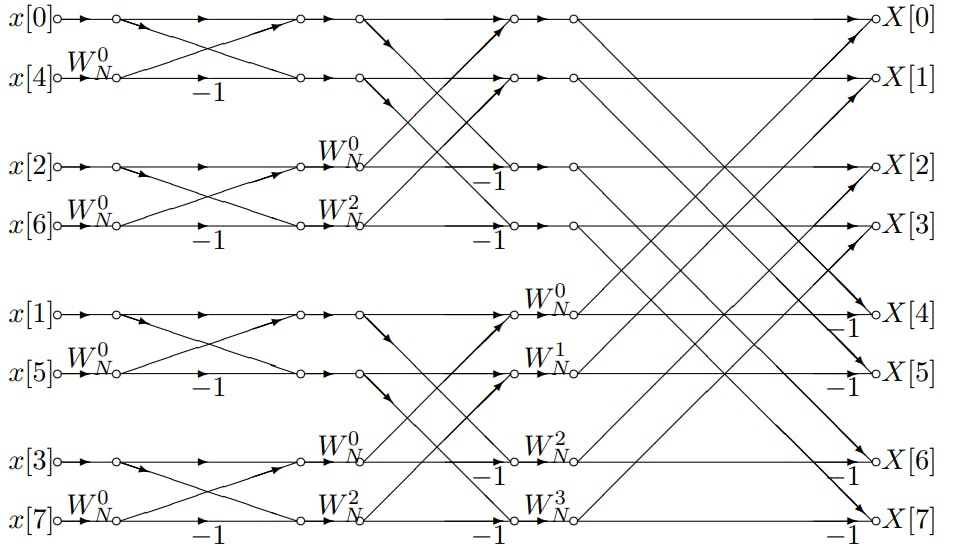

1. DTFT与DFT基本概念

数字信号处理领域中，离散时间傅里叶变换（DTFT）和离散傅里叶变换（DFT）是两种核心的频域分析工具。DTFT提供了一种将离散时间信号映射到连续频域的方法，而DFT则是一种计算离散频域样本的算法，这两个概念虽然紧密相关，但它们在实际应用中具有不同的特点和用途。

1.1 DTFT和DFT的定义及重要性

DTFT是连续频域的变换，对所有离散时间信号都有效。它允许我们研究信号的频谱特性，对于滤波器设计、频谱分析、信号压缩等有着不可替代的作用。相较之下，DFT则为数字信号提供了在计算机上高效进行频域分析的能力，它是离散信号的频域表示，并且在计算机实现时受到时间或数据点数量的限制。

1.2 DTFT与DFT的理论联系

尽管DTFT和DFT在形式上相似，但二者有着本质的区别。DTFT的输出是连续的频谱，而DFT则是离散的。DFT是DTFT的一种近似，可以通过采样定理推导得出。通过理解这两种变换的关系，我们能够更加深刻地把握数字信号处理的核心概念。

在下一章中，我们将深入探索如何在MATLAB中自定义实现DTFT，并探究其理论基础和编程步骤。

2. MATLAB中DTFT的自定义实现方法

2.1 DTFT的基本理论和定义

2.1.1 DTFT的数学定义和物理意义

离散时间傅里叶变换（Discrete-Time Fourier Transform, DTFT）是连续时间傅里叶变换（Continuous-Time Fourier Transform, CTFT）的一种离散形式。它的数学定义为将离散时间信号映射到连续频率上的表示方法。对于任意离散时间信号x[n]，其DTFT X(e^jω) 定义如下：

[ X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n]e^{-j\omega n} ]

其中ω是角频率，j是虚数单位。DTFT的物理意义在于它将离散时间信号转换为连续频率信号，从而允许我们分析信号的频率内容。这在数字信号处理中是至关重要的，因为现实世界的信号通常是连续的，而数字系统处理的信号是离散的。

2.1.2 DTFT与连续时间傅里叶变换的关系

DTFT与CTFT之间的关系很紧密。当信号是连续的而且在所有时间上都存在时，我们可以使用CTFT进行分析。但当信号是离散的，或者我们只能在特定时间点获取信号值时，我们必须使用DTFT。在实际应用中，由于数字系统无法处理无限长的信号，我们通常需要对信号进行截断，这会导致频谱泄露和混叠等现象，因此理解DTFT对于设计数字信号处理系统具有重要意义。

2.2 MATLAB实现DTFT的步骤

2.2.1 离散信号的准备和表示方法

在MATLAB中，我们首先需要准备一个离散信号。这可以通过直接定义一个数组来完成，也可以从实验或测量中获取数据。例如：

n = 0:100; % 时间序列
x = 0.5*sin(2*pi*0.1*n) + 0.2*sin(2*pi*0.3*n); % 离散信号

在这里，我们创建了一个包含101个样本点的信号，这个信号是由两个不同频率的正弦波组成。

2.2.2 使用MATLAB进行DTFT的编程实现

MATLAB没有直接计算DTFT的函数，但我们可以通过使用其快速傅里叶变换（FFT）函数，结合适当的采样来近似DTFT。以下是一段示例代码：

N = 2^14; % 选取FFT的点数
X = fftshift(fft(x, N)); % 计算FFT并进行频移
omega = linspace(-pi, pi, N); % 生成对应的频率向量

在这里，我们首先定义了FFT的点数N，然后使用 fft 函数计算信号的FFT，接着使用 fftshift 将零频率分量移至频谱的中心。最后，我们创建了一个线性空间来表示对应的频率值。通过以上步骤，我们就可以使用FFT来近似DTFT，并可视化信号的频谱。

2.3 DTFT实现中的常见问题及解决方案

2.3.1 信号截断和窗口函数的影响

当我们在实际应用中对信号进行截断时，不可避免地会引入频谱泄露。这是因为截断相当于在时域中乘以一个矩形窗口，而在频域中它会导致主瓣展宽和旁瓣的出现。为了解决这个问题，可以使用各种窗口函数（如汉宁窗、汉明窗等）来减少频谱泄露。

hanning_window = hanning(length(x))'; % 汉宁窗
x_windowed = x .* hanning_window; % 信号乘以窗口
X_windowed = fftshift(fft(x_windowed, N)); % 计算加窗后的FFT

2.3.2 频率分辨率和采样率选择对DTFT的影响

频率分辨率是指FFT结果中能够区分的两个不同频率的最小间隔。它由信号的采样率（Fs）和FFT的点数（N）决定，计算公式为Fs/N。因此，增加FFT的点数或提高采样率可以改善频率分辨率。然而，增加点数或采样率都会增加计算的复杂度和数据量。

Fs = 1000; % 定义采样率
omega_res = Fs/N; % 计算频率分辨率

增加FFT的点数可以提高频率分辨率，但这也会导致更长的计算时间。因此，在实际应用中需要权衡频率分辨率和计算效率。

以上内容即为第二章的核心部分，从基本理论出发，逐步深入到MATLAB中DTFT的自定义实现方法，并对实现过程中可能遇到的问题提供了相应的解决方案。在下一章节中，我们将继续探索DFT在MATLAB中的实际应用，及其与DTFT之间的关系。

3. 使用 fft 函数执行DFT

数字信号处理中，离散傅里叶变换（DFT）是分析信号频谱的关键工具。尽管直接计算DFT在大型数据集上效率不高，但快速傅里叶变换（FFT）算法显著提高了其计算速度。MATLAB中的 fft 函数是实现这一算法的便捷方式，它使用优化的算法来减少计算步骤，从而加速DFT的执行。接下来我们将深入探讨 fft 函数的使用、参数设置以及结果解释和应用。

3.1 DFT的数学公式和算法原理

3.1.1 DFT的定义及其与DTFT的区别

DFT是将时域中的离散信号映射到频域的过程。对于长度为N的复数或实数序列 x[n] ，DFT定义为：

[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn} ]

其中， k 是频率索引（ 0 ≤ k ≤ N-1 ）， j 是虚数单位， N 是样本总数。

与DTFT相比，DFT有三个主要区别：DFT仅对有限长序列进行变换，而DTFT理论上可以应用于无限长序列；DFT的变换结果是N个离散的复数，而DTFT的结果是连续的；DFT假设输入序列是周期性的，而DTFT没有这个假设。

3.1.2 快速傅里叶变换(FFT)的优化算法

FFT是DFT的一种高效计算方法，由Cooley和Tukey于1965年提出。其核心思想是将原始的DFT分解为更小的DFT，通过这些更小的DFT的组合来获得原始DFT的结果，大大减少了计算量。对于长度为N的序列，原始DFT需要的计算复杂度为O(N^2)，而FFT算法仅需要O(NlogN)。

3.1.3 DFT的实际应用场景

DFT不仅用于频谱分析，还广泛应用于信号压缩、滤波器设计、多速率数字信号处理等领域。在无线通信、音频处理、图像处理等行业中，DFT是不可替代的工具。

3.2 MATLAB中 fft 函数的使用和参数设置

3.2.1 fft 函数的基本用法

在MATLAB中， fft 函数可以方便地计算序列的DFT。例如，对于一个长度为N的向量 x ，可以使用 X = fft(x) 来获得其DFT。这里， X 是一个复数向量，其长度也是N。

如果输入序列 x 是实数序列，其DFT的共轭对称性可以用于节省存储空间和计算时间。在这种情况下，只需要存储一半的频谱信息。

N = 1024; % 定义长度为1024的向量
x = randn(N,1); % 生成一个长度为N的随机实数向量
X = fft(x); % 计算x的FFT

3.2.2 fft 函数的高级选项和性能优化

fft 函数提供了多种参数选项来控制变换的大小和类型。例如，可以通过 fft(x, M) 来计算一个长度为M的FFT，其中M > N时，会在 x 后面补零；M < N时，则对 x 进行截断。此外，还可以使用 fft(x, M, dim) 对多维数组沿指定的维度 dim 进行变换。

性能优化方面，为了获得最佳的计算速度，应尽量使用2的幂次长度的序列进行FFT计算。如果序列长度不是2的幂次，MATLAB会自动对序列进行补零以达到最近的2的幂次长度。

3.3 DFT结果的解释和应用

3.3.1 DFT结果的幅度和相位分析

DFT结果由复数表示，包含了信号幅度和相位两个方面的信息。幅度谱表示了信号在各个频率上的能量分布，相位谱则反映了信号中各个频率分量相对于原点的相位偏移。

X_mag = abs(X); % 计算幅度谱
X_phase = angle(X); % 计算相位谱

3.3.2 fft 结果与DTFT结果的比较

在实际应用中，由于 fft 函数计算的是DFT，因此只能得到离散的频谱。理论上，DTFT能够提供连续的频谱信息。在频域分辨率足够高的情况下，DFT结果趋近于DTFT的结果。但当分辨率不足时，两者之间会出现差别。

为了比较 fft 和DTFT，可以使用MATLAB中的 fftshift 函数对FFT结果进行中心化处理，使得零频率分量位于中心。然后与通过DTFT计算的连续谱进行对比，观察分辨率和频谱泄露等效应。

总结

MATLAB中的 fft 函数是高效执行DFT的工具，通过简单的函数调用即可获得复杂DFT运算的结果。在处理实际信号时，理解其基本原理、参数设置以及结果解释是非常重要的。通过合理使用FFT算法，可以在减少计算量的同时获得精确的频谱信息，这对于频域分析和信号处理具有重要意义。在下一章中，我们将通过 testdata.mat 文件进一步探索DTFT与DFT分析的应用。

4. testdata.mat 文件的作用

4.1 testdata.mat 文件的结构和内容

4.1.1 testdata.mat 文件的生成和加载过程

在MATLAB环境中， .mat 文件是一种用于存储工作空间变量的二进制文件格式。 testdata.mat 文件通常用于存储测试数据，以便于在教学和实验中复用和共享。为了生成 testdata.mat 文件，可以遵循以下步骤：

1. 创建信号 ：首先在MATLAB中创建一个或多个信号。这可能包括简单的正弦波、随机噪声或其他复杂的信号。 matlab t = 0:0.001:1; % 时间向量，从0到1秒，采样间隔为0.001秒 x = sin(2*pi*50*t) + 0.5*randn(size(t)); % 创建一个频率为50Hz的正弦波信号，并加入随机噪声

2. 保存信号 ：使用 save 函数将创建的信号存储到 .mat 文件中。 matlab save('testdata.mat', 'x', 't'); % 保存信号x和时间向量t

3. 加载文件 ：在需要使用这些信号进行DTFT或DFT分析时，可以使用 load 函数加载 .mat 文件。 matlab load('testdata.mat'); % 加载testdata.mat文件中的数据

4.1.2 文件中数据的分析和理解

加载 testdata.mat 文件后，MATLAB工作空间将包含与文件同名的变量。例如，在上述例子中，将会得到两个变量：时间向量 t 和信号 x 。可以通过以下命令查看变量的内容：

whos % 查看工作空间所有变量的名称和详细信息

为更深入理解数据，可以绘制信号的图形：

figure; % 创建一个新图形窗口
plot(t, x); % 绘制信号x随时间t的变化图
xlabel('Time (s)'); % 设置x轴标签
ylabel('Amplitude'); % 设置y轴标签
title('Signal x(t)'); % 设置图形标题

通过这些步骤，我们不仅生成和加载了 testdata.mat 文件，而且还可以对其中的数据进行初步的分析和可视化。

4.2 利用 testdata.mat 进行DTFT和DFT分析

4.2.1 使用 testdata.mat 中的信号进行DTFT分析

DTFT分析可以通过自定义函数或MATLAB内置的工具来进行。为了使用 testdata.mat 中的信号进行DTFT分析，可以编写一个自定义函数，该函数使用信号数据和采样频率进行离散时间傅里叶变换。以下是一个简单的DTFT分析的MATLAB代码示例：

function [X, f] = dtft(signal, Fs)
    N = length(signal);
    n = 0:N-1;
    t = n / Fs; % 时间向量
    T = 1 / Fs; % 采样周期
    e = exp(-1j*2*pi*t'); % 复指数向量
    X = signal * e; % DTFT计算
    f = Fs * (-N/2:N/2-1)/N; % 频率向量
end

调用这个函数并传入信号 x 和采样频率 Fs ：

[X, f] = dtft(x, 1000); % 假定采样频率Fs为1000Hz
figure;
plot(f, abs(X)); % 绘制DTFT结果的幅度谱
xlabel('Frequency (Hz)');
ylabel('Magnitude');
title('DTFT Magnitude Spectrum');

通过上述步骤，我们可以得到 testdata.mat 中信号的DTFT幅度谱。

4.2.2 使用 testdata.mat 中的信号进行DFT分析

DFT分析通常使用MATLAB内置的 fft 函数来执行，它是一种快速的算法，用于计算信号的离散傅里叶变换。以下是使用 testdata.mat 文件中的数据进行DFT分析的示例：

N = length(x); % 信号长度
n = 0:N-1; % 时域索引
k = n'; % 频域索引
X_k = fftshift(fft(x)); % 使用fftshift进行频率中心化
f = (-N/2:N/2-1)*(Fs/N); % 频率向量

figure;
plot(f, abs(X_k)); % 绘制DFT幅度谱
xlabel('Frequency (Hz)');
ylabel('Magnitude');
title('DFT Magnitude Spectrum');

通过执行上述代码，我们可以得到 testdata.mat 中信号的DFT幅度谱。

4.3 testdata.mat 在教学和实验中的应用案例

4.3.1 作为教学工具在课堂上的使用

testdata.mat 文件可以作为教学工具，通过实际案例帮助学生理解信号处理的基本概念，例如频谱分析、信号的时域和频域表示等。以下是在教学中使用 testdata.mat 进行DTFT和DFT演示的示例：

在课堂上，教师可以首先通过加载 testdata.mat 文件并展示信号的时域波形，然后引导学生一起编写DTFT和DFT的MATLAB代码，最后展示分析结果。这种互动式教学不仅能够提高学生的参与度，而且加深他们对理论的理解。

4.3.2 实验验证中 testdata.mat 的作用和效果

在进行实验验证时， testdata.mat 文件能够提供一个标准的数据集，学生可以通过这个数据集来验证他们的DTFT和DFT实现是否正确。实验的步骤可以包括：

1. 加载 testdata.mat 文件。
2. 应用自定义的DTFT分析函数来计算信号的频谱。
3. 使用MATLAB内置的 fft 函数对同一信号进行频谱分析。
4. 对比两个分析结果，验证DTFT和DFT的实现正确性。

通过这样的实验，学生不仅能掌握DTFT和DFT的理论知识，还能加深对MATLAB软件工具的使用经验。

5. DTFT公式细节

5.1 DTFT公式的深入解析

5.1.1 离散时间傅里叶变换公式的详细推导

离散时间傅里叶变换（DTFT）是一种将离散时间信号从时域转换到频域的数学工具。它的公式定义如下：

[ X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n]e^{-j\omega n} ]

这里，( X(e^{j\omega}) ) 表示信号 ( x[n] ) 的傅里叶变换。 ( \omega ) 是数字角频率，( j ) 是虚数单位。

推导过程起始于对于周期信号的傅里叶级数，而 DTFT 可以看作是傅里叶级数的极限形式，其中信号扩展为非周期，频率变量 ( \omega ) 变为连续。推导的基本思想是利用信号的内积定义，将离散信号通过复指数基函数进行展开。

5.1.2 DTFT变换性质的理论探讨

DTFT 具有多种重要的性质，这些性质在信号分析和系统分析中至关重要。包括线性、时移、频移、卷积以及能量守恒等性质。具体如下：

• 线性：如果 ( X(e^{j\omega}) = DTFT{x[n]} )，且 ( Y(e^{j\omega}) = DTFT{y[n]} )，那么对于任意的常数 ( a ) 和 ( b )，有 ( DTFT{ax[n] + by[n]} = aX(e^{j\omega}) + bY(e^{j\omega}) )。
• 时移：( DTFT{x[n - n_0]} = e^{-j\omega n_0}X(e^{j\omega}) )，这说明信号的时移在频域表现为相位的变化。
• 频移：( DTFT{x[n]e^{j\omega_0 n}} = X(e^{j(\omega - \omega_0)}) )，信号在时域乘以复指数相当于频域内的平移。
• 卷积：( DTFT{x[n] * h[n]} = X(e^{j\omega})H(e^{j\omega}) )，这是信号处理中的一个关键性质，允许通过频域运算来实现时域中的卷积运算。
• 能量守恒：( \sum_{n=-\infty}^{\infty} |x[n]|^2 = \frac{1}{2\pi} \int_{-\pi}^{\pi} |X(e^{j\omega})|^2 d\omega )，即信号的能量在时域和频域内是相等的。

5.2 DTFT公式的应用和数值计算

5.2.1 利用DTFT公式解决实际问题

在实际应用中，DTFT可以用于滤波器设计、信号识别、频谱分析等。例如，在无线通信领域，DTFT可以用来分析信号的频谱特性，以确定通信系统的带宽需求。在音频处理中，DTFT可用于分离出信号中的不同频率成分，这对于音乐和语音分析尤为重要。

5.2.2 数值计算方法和DTFT公式的计算机实现

由于DTFT涉及到无限长信号，因此在计算机上实现时通常要对信号进行截断，这引入了所谓的频谱泄露问题。一种常用的解决方法是应用窗函数来减少泄露效应。此外，当需要计算大量数据的DTFT时，可以使用快速傅里叶变换（FFT）算法来提高效率。

MATLAB代码示例：

% 定义离散信号和窗函数
n = 0:1023; % 信号长度
x = cos(0.2*pi*n) + 0.5*sin(0.3*pi*n); % 信号示例
w = hamming(length(x)); % 使用汉明窗

% 应用窗函数并进行DTFT
X = fftshift(fft(w.*x));

% 绘制DTFT的幅度谱
f = (-length(x)/2:length(x)/2-1)*(1/(length(x)*0.01)); % 频率范围
plot(f, abs(X));
xlabel('Frequency (Hz)');
ylabel('Amplitude');

5.3 DTFT公式的局限性和扩展

5.3.1 DTFT公式的局限性分析

DTFT的主要局限性在于它要求处理无限长的信号，这对于实际中的有限长信号来说是不现实的。此外，DTFT产生的频谱是连续的，而在数字系统中，我们只能处理有限数量的离散频率点。

5.3.2 离散傅里叶级数(DFS)和DTFT的关系

为了克服DTFT的局限，离散傅里叶级数（DFS）被引入，它专门处理周期信号的频谱分析。当一个周期信号是采样得到的，我们得到的就是DFS的样本点。DFS可以看作是DTFT在周期信号上的特例，而DTFT则可以看作DFS在非周期信号上的推广。

在实际应用中，我们通常使用FFT来近似计算DFS或DTFT，这可以显著提高计算效率。 FFT算法使得频域分析变得更加高效，特别是当需要处理大量数据时。

通过以上章节的深入分析，我们不仅掌握了DTFT公式的理论基础，同时也探索了它在实际应用中的价值和局限性。DTFT不仅在信号处理领域，而且在许多工程应用中发挥着重要作用，它为我们提供了一种强大的工具来分析和理解信号的频率特性。

6. DFT与DTFT的关系及逆变换

6.1 DFT与DTFT的关系探究

在数字信号处理中，DFT与DTFT之间的关系是核心概念之一。理解两者之间的联系对于应用频域分析方法至关重要。

6.1.1 DFT作为DTFT的采样

DFT实际上是对DTFT的一种采样。在连续频率域中，DTFT产生一个连续的谱。而DFT则是在一系列离散的频率点上对DTFT进行采样。如果我们设定了一个固定长度的离散时间信号，其长度为N，并且我们按照一个固定频率F_s采样，那么我们可以得到DFT的频率分辨率Δf = F_s/N。这表明DFT仅能分辨间隔为Δf的频率分量。

6.1.2 采样定理和DFT对DTFT的近似

根据采样定理，如果信号的最高频率分量不超过F_s/2，那么该信号可以通过采样来无失真地重建。DFT通过在等间隔的频率点上对DTFT进行采样，近似了连续的DTFT谱。然而，由于DFT的有限长度，它不能完全代表DTFT。为了解决这个问题，可以应用窗函数来减少信号截断带来的频谱泄露。

6.2 逆变换的理论和实现

逆变换在信号处理中占有重要地位，它允许我们从频域转换回时域，进行信号重构。

6.2.1 DTFT的逆变换公式和其物理意义

DTFT的逆变换公式允许我们从频率谱中恢复出原始的时域信号。数学表达式如下：

x[n] = (1/2π) ∫ from -π to π X(e^jω) e^(jωn) dω

其中，X(e^jω)表示频率谱，x[n]是时域信号。这个公式的物理意义是，通过频率谱和复指数函数的乘积来重建时域信号。

6.2.2 DFT的逆变换和IFFT的实现方法

DFT的逆变换通常称为IDFT（Inverse Discrete Fourier Transform），在MATLAB中可以通过IFFT函数来实现。IFFT是DFT的快速逆变换算法，和FFT类似，大大提高了运算效率。IFFT的数学表达式和执行逻辑说明如下：

x[n] = (1/N) ∑ from k=0 to N-1 X[k] e^(j2πkn/N)

其中，X[k]是DFT变换结果，x[n]是逆变换后的时域信号。

在MATLAB中，如果有一个DFT变换后的向量X，可以使用以下代码进行IFFT操作：

x = ifft(X, 'symmetric');

代码中的 'symmetric' 参数确保结果是实数值，符合物理信号的特性。

6.3 逆变换在信号处理中的应用

逆变换在信号处理的许多方面都发挥着重要作用，特别是在信号重构和系统识别中。

6.3.1 信号重构和噪声去除

在信号传输或存储过程中，可能会对信号进行编码，添加一些冗余信息以进行错误校正或增强信号的鲁棒性。逆变换可以用来去除这些冗余信息，重构原始信号。同时，在某些情况下，逆变换还可以辅助信号去噪，通过滤除某些频率分量来清除噪声。

6.3.2 系统识别和参数估计中的逆变换应用

逆变换对于系统识别和参数估计非常有用。例如，在通信系统中，可以通过发送一个已知的测试信号，然后通过逆变换来分析系统的冲击响应。通过分析这些数据，工程师可以评估系统的性能，甚至提取出系统参数进行优化。

逆变换与IFFT在MATLAB中的应用示例如下：

% 假设信号x已经被DFT变换并存储在向量X中
% 使用IFFT进行逆变换
x_reconstructed = ifft(X);

% 重建的信号x_reconstructed可以用来进行信号重构或去噪处理

通过以上分析，我们已经理解了DFT与DTFT之间的关系以及逆变换的应用。在后续章节中，我们将探讨如何利用这些理论在实际中解决问题。

本文还有配套的精品资源，点击获取

简介：DTFT是将离散时间信号转换到频率域的信号处理概念，而DFT是其在周期延拓下的离散版本，广泛用于数字信号处理。本简介探讨了在MATLAB环境下DTFT的自定义函数实现以及DFT的标准函数 fft ，并通过 testdata.mat 文件中的测试数据验证了这些函数的正确性。文章强调了DTFT与DFT的重要概念，包括DTFT公式、周期性、DFT与DTFT的关系、逆变换、傅里叶变换性质，以及在多个信号处理领域的应用实例。

本文还有配套的精品资源，点击获取