随机计算（1）——新的开始

Review of Stochastic Computing

导师上周给我发了一系列的论文，这也算是正式开始我PhD科研生涯开始的标志。我导师研究的是随机计算和近似计算，由于我本科期间是通信专业的，所以先让我研究随机计算，更多用到模拟信号的知识，方便入门些。下面进入正题：

Introduction

现在流行的计算硬件发展受限于一些现实的应用条件：小尺寸，低功耗，高可靠性。同时，它还存在一些物理现象：工业制造过程中的变化和软错误。这些物理现象都易于产生错误，不过它们可以通过概率论中的理论来进行描述。因此，接下来描述的随机计算 也引起了人们的研究兴趣。

随机计算最重要的特征：SC的一个基本特征是数字由可以由非常简单的电路处理的比特流表示，而数字本身被解释为概率，即这串比特流中每一个比特为1的概率，而利用伯努利大数定律，概率可以用频率来估计，即每一位比特为1的概率可以用这串比特流中的1的个数在比特流中的占比来表示。 举个例子来说：
（1，0，0，0）：0.25（$\frac{1}{4}$）
（0，1，0，0）：0.25（$\frac{1}{4}$）

特征1

SC(之后下文中都用SC代替Stochastic Computing)从上世纪60年代刚引入开始，它的第一个吸引点是可以使用基础的逻辑门搭建一个成本低的具有算术功能的电路。例如：乘法 在SC中可以通过一个与门 来实现

Figure 1

与门实现的功能可以用概率描述为：
$$P(S_3=1)=P(S_1=1)\ast P(S_2=1)$$
用SN（Stochastic Number）描述为：
$$S_3=S_2\ast S_1$$
但是这样的运算若要求准确是需要条件的，例如下面：

Figure 2

可以注意到在这个算术电路中，运算结果是不正确的。这里提前说一下，若要AND门利用SC理论准确表示乘法运算，需要两个输入比特流X,Y是不相关的或者独立的。

特征2

SC的另外一个吸引人的特征是容错能力，尤其是因为由过程变化或宇宙辐射引起的瞬态或软错误。例如：
在Figure 1 中如果输出比特流中有一个比特位状态翻转，那个它的值只会从$\frac{3}{8}$ 变成$\frac{4}{8}$ 或$\frac{2}{8}$. 但是如果是在传统的二进制表示形式中，一个比特位的变化会引起很大的变化。

问题1

SC同样也存在一些问题影响它实际的应用。SC计算精度的增长会导致比特流长度的指数速度增长。例如，若要求计算精度从4变成8，比特流长度需要从$2^4=16$ 变成$2^8=256$,从而也导致计算时间呈指数增长，使得处理时间变长。

问题2

它的准确性较低，毕竟都是概率性的。

问题3

复杂的设计需求。在后面将提到SC电路设计包括Reconfigurable Design, Fixed Design, Combinational Logic Design and Sequential Logic Design。

Basic Concepts

Scaled Add

由于SN(Stochastic Number)实际是用来表示概率的，所以它的范围是在[0,1]。也因此两个数的加法运算不方便，因为和的范围在[0,2]内。SC采用了特殊的Scaled add操作来解决这个问题。如下：

Figure 3
$$P(S_4)=P(S_3)P(S_1)+(1-P(S_3))P(S_2)=(P(S_1)+P(S_2))/2$$

Convert binary numbers to stochastic numbers and vice versa

Figure 4. Number conversion circuits: (a)binary-to-stochastic; (b)stochastic-to-binary
Figure 4(a) 展示了一个广泛运用的二进制数-随机数之间转换的转换电路，被称为SNG(Stochastic Number Generator)。这个电路包含二个主要部分：（伪）随机数产生器，比较器。
若随机产生器产生$m$位的二进制数，那么一个周期内每一个产生的数的概率是$\frac{1}{2^m}$。而比较器的作用是当随机数小于x时，输出1。那么输出1的概率就是$\frac{x}{2^m}$，表现在输出序列上就是一个长为$2^m$的比特流序列，1所占的比例是$\frac{x}{2^m}$。
Figure 4(b)是一个随机数-二进制数的转换电路。原理是SN作为Counter(计数器)的使能信号，一串比特流序列中有多少个1那么计数器就在一个计数周期内计数多少次，从而转变成二进制数。

Different SN Formats

IBP在后面的Fixed Circuit设计中起到重要的作用。部分Gate的运算在不同的域不一样：XOR(IBP: Multiplication), XNOR(BP: Multiplication)。特例是：MUX(UP, BP, IBP: Add)。

Accuracy Problem

Figure 4 Stochastic circuit realizing the arithmetic function $z=x_1{x}_2{x}_4+x_3(1-x_4)$
在图四中已经选择了适当的SN来避免不准确的问题。实际上，即使我们选择高质量的随机数来产生SN，例如：
$$\begin{gathered} S_1=(0,1,1,0,0,0,1,0),S_2=(0,0,1,1,1,1,1,1) \\ {S}_3=(1,1,1,1,1,1,1,1),S_4=(0,0,0,0,0,0,0,0) \end{gathered}$$
可以得到：$S_6=(1,1,1,1,1,0,1,1)=\frac{7}{8}̸=\frac{6}{8}$

原因：
1、由于随机数的固有的抖动
例如在这个例子中$S_6$可以准确获得6个“1”的概率是：
$$P(z=\frac{6}{8})=\left(\genfrac{}{}{0ex}{}{8}{6}\right)(\frac{6}{8}{)}^6(\frac{2}{8}{)}^2\cong 0.31$$
分析一下这个“抖动”的过程：
设$\hat{p}$表示成为N比特流真实所表示的概率值; $P$表示期望达到的概率值。那么均方差为：$$D(P)=E[(P-\hat{P}{)}^2]=\frac{NP(1-P)}{N^2}$$
（N个独立的伯努利分布变量的和产生的新变量的方差是$NP(1-P)$，然后每个变量$X$都要乘上$\frac{1}{N}$，所以方差乘上$\frac{1}{N^2}，最终得到\frac{P(1-P)}{N}$）

所以SN所表示的概率值收敛到$\hat{P}$的速度为$O(\sqrt{N})$,即SN的精度随着比特流长度的增长而提升也就是说随着时间而改善精度。这个性质被称作：渐进精度。
拓展这个性质，又引入了一个新性质：一致精度。即一串长度为$n$的比特流，如果这串比特流构成的所有SN:${\hat{P}}_k,k=1,2,3,...,{\log }_2(n)$全部相等且等于$\hat{P}$,因为SN的精度和准确度是随着比特流长度增长而增长的，那么这串比特流可以看作是表示这个概率值的最有意义的初始比特流。

2、由于输入序列之间具有相关性
为了解决这个问题，前人定义两串比特流不相关或者独立的定义：
$$\begin{gathered} 定义输入的两个比特流为S_1=(S_1(1),S_1(2),...,S_1(n))and{S}_2=(S_2(1),S_2(2),...,S_2(n)) \\ 当且仅当：\sum _{i=1}^n{S}_{1(i)}{S}_2(i)=\frac{{\sum }_{i=1}^n{S}_1(i)\times {\sum }_{i=1}^n{S}_2(i)}{n}不相关或独立 \end{gathered}$$
注：这和两随机信号不相关是一致的，随机信号中定义：
$$互协方差函数K(t_1,t_2)=E(X(t_1)X(t_2))-m(X(t_1))m(X(t_1))=0时，两随机过程是不相关的$$

为了产生不相关的比特流，SC使用伪随机数产生器（LFSR-线性反馈移位寄存器）。伪体现在：它产生随机数的过程类似n重伯努利实验，所以最后产生的比特流中的“1”和“0”的个数几乎一样；而且它产生的随机数是循环周期的产生，且每个周期内产生数据的顺序是一致的且不重复，因此它可以准确的用一串序列中1的个数来反映每一位为1的概率，如Figure 1中的电路结构。

设计一种利用LFSR产生任意SN的SNG：

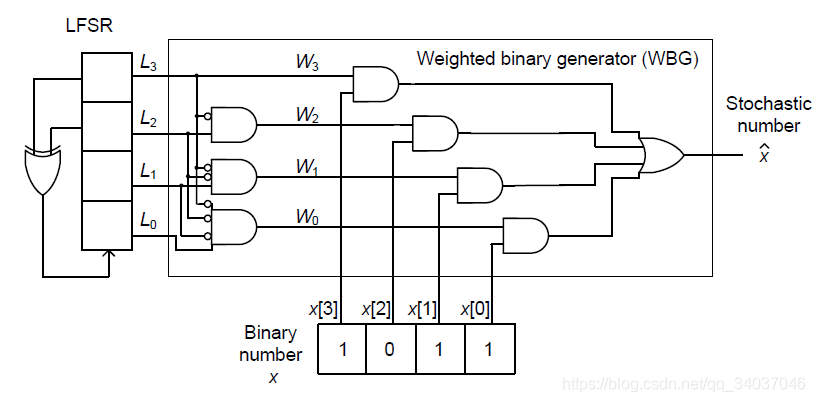
Figure 5 SNG Using Linear Feedback Shift Register
提示：$L_3,L_2,L_1,L_0均互不相关$
$$\begin{gathered} W_3=L_3 \\ {W}_2=(1-L_3)L_2 \\ {W}_1=(1-L_3)(1-L_2)L_1 \\ {W}_0=(1-L_3)(1-L_2)(1-L_1) \end{gathered}$$
根据互不相关SN的性质可得：$P_3=\frac{1}{2},P_2=\frac{1}{4},P_1=\frac{1}{8},P_0=\frac{1}{16}$，其实这4个$W_i$没有交叠的“1”，可以类比成概率论中的互不相容时间，最后得到的$\hat{X}\approx X$。
在实际SC电路中，如果需要多个独立的SN，如果是采用多个SNG，则成本太高了，所以也可以采用以下电路：

当然，如果我们的运算中包含乘法运算，则输入序列需要不相关。但有时我们也需要合理利用不相关，例如像在多路选择器MUX中，便不需要输入序列互不相关。在XOR中，如果输入序列具有最大的互相关性，则运算可表示为**$|X-Y|$**。

Design

Reconfigurable stochastic circuits

将一般函数利用优化理论逼近为一个贝恩斯坦多项式，求得最优的贝恩斯坦多项式系数，电路图如下：

Figure 6 Reconfigurable Design
DGC中实际是一个加法器。$P(S=i)=\left(\genfrac{}{}{0ex}{}{n}{i}\right)(X{)}^i(1-X{)}^{m-i}$。
从而$Y={\sum }_0^{i=m}{B}_i\left(\genfrac{}{}{0ex}{}{n}{i}\right)(X{)}^i(1-X{)}^{m-i}$。

Fixed stochastic circuits

利用IBP形式的SN来进行设计电路。此处略。
电路图如下：

Figure 7 Fixed Design

Application

Filter design

Image processing

Decoding Error-Correcting Codes

Artificial neural networks

第一次写综述，对着论文写的估计很乱很杂。本来今天给自己的任务就是写完，没想到写到接近五点，仍然亢奋，
但是怕掉头发，最后很多东西都省略了，第一次就自我安慰一下吧。明早直接睡到12点，哈哈哈哈哈哈啊哈~
由于本人水平不高，其中估计有错误，望不吝赐教！
万分感谢。