算法时间复杂度

 这个部分尝试从校内课程入手，然后参考学习算法导论内容，继续开阔自己的眼界。校内课程对应的是高级算法设计，学习的时候多总结、多练习、多回忆应该是有效果的，毕竟这学期时间很紧迫。

 本章主要进行算法复杂性的分析，学习基本的空间复杂度和时间复杂度，并且掌握一些基本的快速估计复杂度的定理、方法。

算法效率分析基础

 算法分析是对一个算法需要多少计算时间和存储空间做定量的分析。

分析框架

输入规模度量

• 算法的时间效率和空间效率都用输入规模的函数进行度量
• 对相同的大小的输入实例具有相同的分析结果
• 对于所有的算法，对于规模更大的输入都需要更长的运行时间
• 经常使用一个输入规模n为参数的函数来研究算法的效率

运行时间的度量单位

• 用算法的基本操作（算法中最重要的操作）的执行次数来度量算法的时间效率
• 基本操作通常是算法的最内层循环中最费时的操作
• 算法运行时间的估计：

$$T(n)\approx c_{op}C(n)$$

n是该算法的输入规模

$c_{op}$ 是特定计算机上一个算法基本操作的执行时间

C(n)是该算法需要执行的基本操作次数

算法的最优、最差、平均效率

• 最差效率是指在输入规模为n的时候，算法在最坏情况下的效率
• 最优效率是指在输入规模为n时，算法在最优情况下的效率
• 平均效率是指在“典型”或“随机”输入的情况下，算法具有的行为（效率）

增长次数

• 小规模输入在运行时间上的差别不足以将高效的算法和低效的算法区分开来

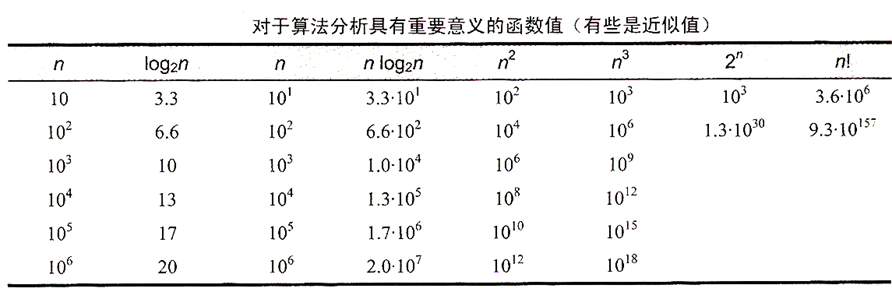
• 指数级操作次数的算法，只能解决规模非常小的问题

指数与多项式

  $2^n$ 与$n^2$ 相比，指数的增长速度是很快的，在算法中应该尽量避免。

数量级的差别

 在很多时候，我们认为$n$ 和$n^2$之间的差异是比较大的，而n和5n之间的差异是较小的甚至可以忽略不计，因此引入渐进表达式来解决这个问题。

渐进表达式

常数间差异较小

 渐进表达式的核心在于忽略掉常数。

渐进分析符号

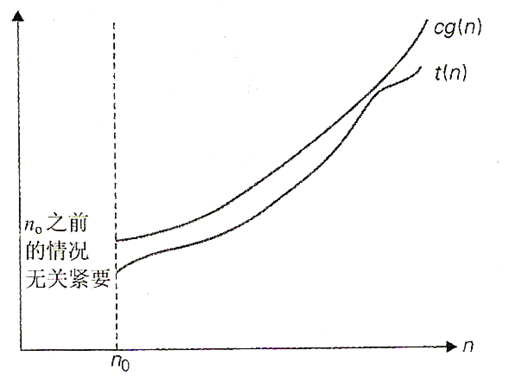
渐进上界符号

 渐近上界符号$O$,存在正常数$c$和$n_0$使得对所有$n\ge n_0$，有
$$f(n)\le cg(n)$$
记为$f(n)\in O(g(n))$

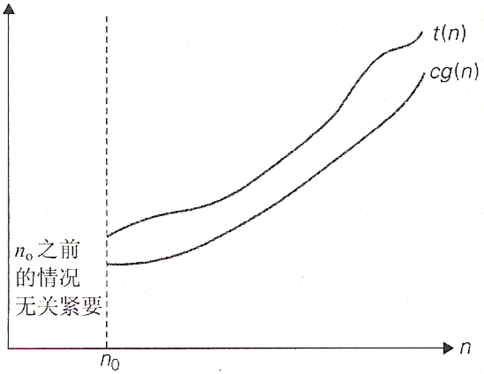
渐进下界符号

 渐进下界符号$\Omega$，存在正常数$c$ 和$n_0$ 使得对所有的$n\ge n_0$有：
$$f(n)\ge cg(n)$$
记为$f(n)\in \Omega (g(n))$

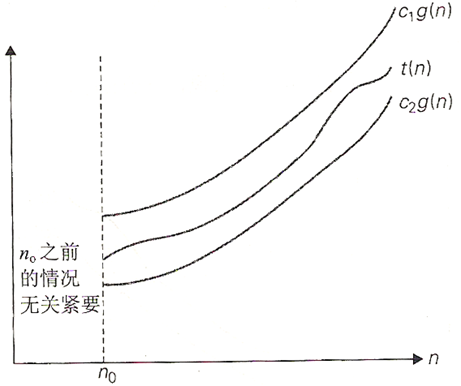
渐进近界符号

 渐进近界符号$\theta$， 存在正常数$c_1$，$c_2$和$n_0$使得对所有的$n\ge n_0$都有：
$$c_{2}g(n)\le f(n)\le c_{1}g(n)$$
记为$f(n)\in \Theta (g(n))$

非紧上界记号

 非紧上界记号$o$，$o(g(n))$ = { $f(n)$ | 对于任何正常数$c>0$，存在正数$n_0>0$使得对所有$n\ge n_0$有：$0\le f(n)<cg(n)$ }，等价于 $f(n)/g(n)\to 0$ ，as $n\to \infty$。

非紧下界记号

非紧下界记号$\omega$，$(g(n))$ = { $f(n)$ | 对于任何正常数$c>0$，存在正数$n_0>0$使得对所有$n\ge n_0$有：$0\le cg(n)<f(n)$ }
等价于$f(n)/g(n)\to \infty$ ，as $n\to \infty$。
$f(n)\in (g(n))\iff g(n)\in o(f(n))$

渐进符号的特性

定理：如果$t_1(n)\in O(g_1(n))$并且$t_2(n)\in O(g_2(n))$，则$t_1(n)+t_2(n)\in O(max(g_1(n),g_2(n))$

• 对于渐进符号$\Omega$，$\Theta$，该定理也成立
• 该定理表明：当算法由两个连续执行部分组成时，该算法的整体效率由具有较大增长次数的那部分所决定

渐进分析中函数的比较

 这个部分可以类比大小的比较进行：
$$\begin{gathered} f(n)=O(g(n))\approx a\le b \\ f(n)=\Omega (g(n))\approx a\ge b \\ f(n)=\Theta (g(n))\approx a=b \\ f(n)=o(g(n))\approx a<b \\ f(n)=\omega (g(n))\approx a>b \end{gathered}$$

渐进符号的性质

传递性

$$\begin{gathered} f(n)=\Theta (g(n))，g(n)=\Theta (h(n))\Rightarrow f(n)=\Theta (h(n)) \\ f(n)=O(g(n))，g(n)=O(h(n))\Rightarrow f(n)=O(h(n)) \\ f(n)=\Omega (g(n))，g(n)=\Omega (h(n))\Rightarrow f(n)=\Omega (h(n)) \\ f(n)=o(g(n))，g(n)=o(h(n))\Rightarrow f(n)=o(h(n)) \\ f(n)=\omega (g(n))，g(n)=\omega (h(n))\Rightarrow f(n)=\omega (h(n)) \end{gathered}$$

反身性

$$\begin{gathered} f(n)=\Theta (f(n)) \\ f(n)=O(f(n)) \\ f(n)=\Omega (f(n)) \end{gathered}$$

对称性

$$f(n)=\Theta (g(n))\iff g(n)=\Theta (f(n))$$

互对称性

$$\begin{gathered} f(n)=O(g(n))\iff g(n)=\Omega (f(n)) \\ f(n)=o(g(n))\iff g(n)=\omega (f(n)) \end{gathered}$$

算术运算

$$\begin{gathered} f(n)+g(n)=O(f(n)+g(n)) \\ f(n)\ast g(n)=O(f(n)\ast g(n)) \\ cf(n)=O(f(n)) \\ g(n)=O(f(n))\iff f(n)+g(n)=O(f(n)) \end{gathered}$$

习题

 1、给定$f1(n)=O(f(n))$ ，$g_1(n)=O(g(n))$ ，请证明$f_1(n)+g_1(n)=O(f(n)+g(n))$

 2、已知$g(n)=O(f(n))$ ，证明 $f(n)+g(n)=O(f(n))$

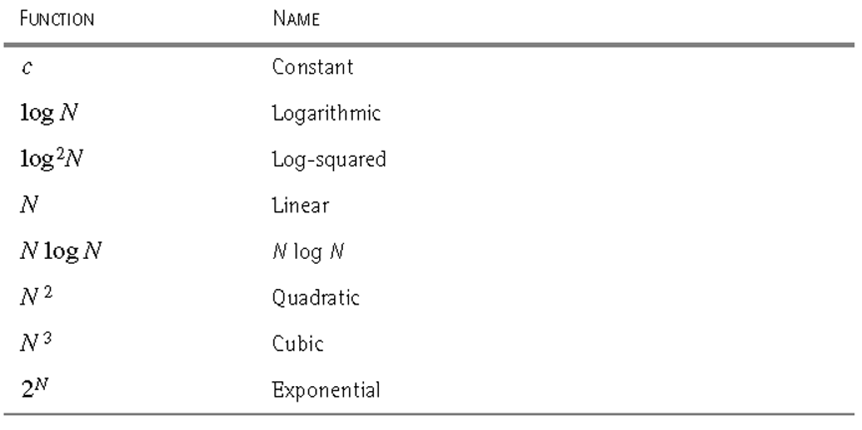
基本效率类型

 常量($c$) < 对数($logn$) < $lo{g}^{2}n$ < 线性($n$) < $nlogn$ < 平方($n^2$) <立方($n^3$) < 指数($2^n$) < 阶乘($n!$)

多项式

 给定一个非负整数$d$，$n$的$d$次多项式为具有以下形式的一个函数$p(n)$：
$$p(n)=\sum _{i=0}^d{a}_i{n}^i$$
其中常量$a_0,a_1,...,a_d$是多项式的系数且$a_i\ne 0$。一个多项式为渐进正的当且仅当$a_d>0$。对于一个$d$次渐进正的多项式$p(n)$，有$p(n)=\Theta (n^d)$。对任意实常量$a\ge 0$，函数$n^a$单调递增，对任意实常量$a\le 0$，函数$n^a$单调递减。若对某个常量$k$，有$f(n)=O(n^k)$，则称函数$f(n)$是多项式有界的。

指数

 可以通过下边儿的极限，讲多项式与指数的增长率互相关联。对所有使得$a>1$的实常量$a$和$b$，有
$$\underset{n\to \infty }{\lim }\frac{n^b}{a^n}=0$$
根据此可以得知：
$$n^b=o(a^n)$$
因此，任意底大于1的指数函数比任意多项式函数增长得快。

对数

 若对某个常量$k$，$f(n)=O({\lg }^{d}n)$则称函数$f(n)$是多对数有界的。可以通过下列极限，将多项式与多对数的增长互相关联：
$$\underset{n\to \infty }{\lim }\frac{{\lg }^{b}n}{(2^a{)}^{\lg n}}=\underset{n\to \infty }{\lim }\frac{{\lg }^{b}n}{n^a}=0$$
根据这个极限，我们可以得到：对任意常量$a>0$，
$${\lg }^{b}n=o(n^a)$$
因此，任意正的多项式函数都比任意多对数函数增长得快。

阶乘

 记号$n!$定义为对整数$n\ge 0$，有
$$n!=\{\begin{array}{l}1，若n=0\\ n(n-1)!，若n>0\end{array}$$
 阶乘函数的一个弱上界是$n!\le n^n$，因为在阶乘中，$n$项的每项最多为$n$。斯特林近似公式
$$n!=\sqrt{2\pi n}(\frac{n}{e}{)}^n(1+\Theta (\frac{1}{n}))$$
给出了一个更紧确的上界和下界，其中$e$是自然对数的地。
$$\begin{gathered} n!=o(n^n) \\ n!=\omega (2^n) \\ \lg (n!)=\Theta (n\lg n) \end{gathered}$$

多重函数

 我们使用记号$f^{(i)}(n)$来表示函数$f(n)$重复$i$次作用于一个初值$n$上。形式化的，假设$f(n)$为实数集上的一个函数。对非负整数$i$，我们递归的定义:
$$f^{(i)}(n)=\{\begin{array}{l}n若i=0\\ f(f^{(i-1)}(n))若i>0\end{array}$$
例如，若$f(n)=2n$，则$f^{(i)}=2^{i}n$。

多重对数函数

 我们使用${\lg }^{\ast }n$（读作“$\log$星$n$”）来表示多重对数，定义多重函对数函数为
lg ⁡ ∗ n = m i n { i ≥ 0 : lg ⁡ ( i ) ≤ 1 } \lg^* n = min\{ i \geq 0: \lg^{(i)} \leq 1\} lg∗n=min{i≥0:lg(i)≤1}
注意：区分${\lg }^{(i)}n$（从参数$n$开始，连续应用对数函数$i$次）与${\lg }^{i}n$（$n$的对数的$i$次幂）。多重对数是一个增长非常慢的函数。

渐进增长率比较的三种方法

1、定义法

 找到正常数$c$和$n_0$使得对所有$n\ge n_0$有$f(n)\le cg(n)$，则
$$f(n)=O(g(n))$$

2、极限法

 比较两个函数$f(n)$和$g(n)$的渐近增长率时，可以对两个函数相除，然后令变量$n$趋向于无穷，看这个极限值是无穷大还是一个大于零的常数还是趋向于0。

 比如，当
$$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=0$$
则 $f(n)=O(g(n))$

前两种情况意味着t(n) ∈ O(g(n))
后两种情况意味着t(n) ∈ Ω(g(n))
第二种情况意味着t(n) ∈ Θ(g(n))

3、取对数法

 对于比较难的比较的两个函数，我们可以对它们同时取对数后再进行比较，比如：
$$(logn{)}^{3n}{2}^{n\log n}$$

例题

 对下列函数按渐进关系O从小到大排列：
$$\begin{gathered} f_1(n)=10^n{f}_2(n)=n^{1/3} \\ {f}_3(n)=n^n{f}_4(n)=lo{g}_{2}n \\ {f}_5(n)=2^{\sqrt{lo{g}_{2}n}} \end{gathered}$$