扩展欧几里得算法

本文的问题场景中，涉及到的变量均为整数。

扩展欧几里得算法的内容及证明

贝祖等式：
$$ax+by=gcd(a,b)=c$$
其中 $a$ 和 $b$ 为已知值， $c$ 为 $a$ 和 $b$ 的最大公约数。 $x$ 和 $y$ 为要求的方程变量。

贝祖等式就是说上述式子一定有解。

扩展欧几里得算法(贝祖等式)的证明：

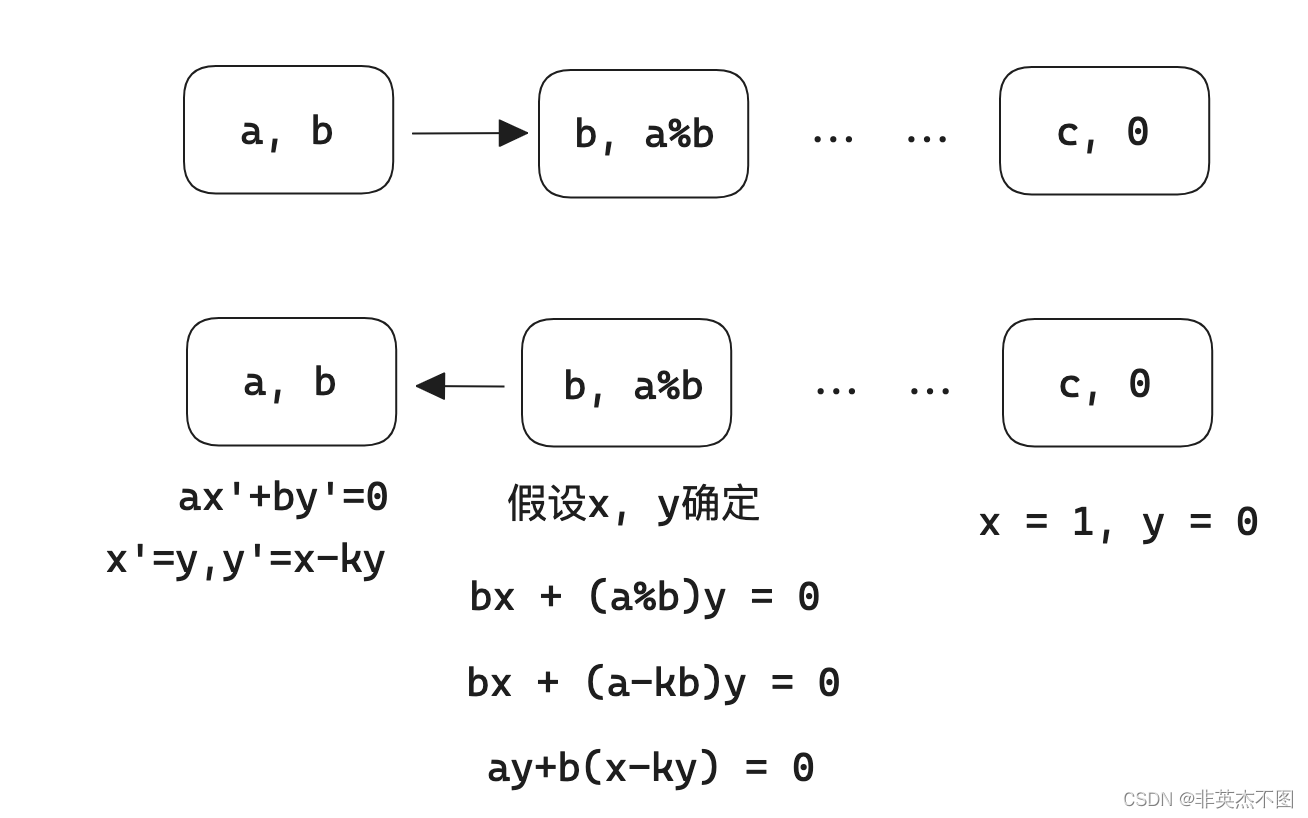
由上一篇文章(欧几里得算法) 可知，$gcd(a,b)=gcd(b,a\%b)$. 这样不断递归下去，最终能得到 $gcd(a,b)=gcd(b,a\%b)=...=gcd(c,0)$

然后在回溯的过程中，假设$a=c,b=0$, 那么很容易得知当$x=1,y=0$ 时， 有 $ax+by=c$; 数学归纳法的思路，假设回溯在某一层 $(b,a\%b)$ 时， 已经确定了 $x$ 和 $y$, 即
$$\begin{array}{r}bx+(a\%b)y=c\end{array}$$
那么对于回溯的下一层 $(a,b)$ , 需要确定 $x^{\prime },y^{\prime }$， 使得
$$\begin{array}{r}a{x}^{\prime }+b{y}^{\prime }=c\end{array}$$
因为 $a % b $ 可以写成 $a-kb$ 的形式，所以 $(1)$ 式可以写为:

$$bx+(a-kb)y=c$$

整理得

$$\begin{array}{r}ay+b(x-ky)=c\end{array}$$

于是令 $x^{\prime }=y,y^{\prime }=x-ky$ 即可使得 $(2)$ 式成立。

如下图所示：

这样贝祖等式就证明了一定有解，并且找到了一种求解的方式。这也就是扩展的欧几里得算法。

扩展欧几里得算法的代码实现

代码实现：

#include <iostream>

using namespace std;
int ex_gcd(int a, int b, int &x, int &y) {
	if (b == 0) {
		x = 1, y = 0;
		return a;
	}
	int x1, y1;
	int r = ex_gcd(b, a % b, x1, y1);
	x = y1, y = x1 - a / b * y1;  //对应上面的公式,k=a/b
	return r;

}


int main() {
	int a, b;
	while (cin >> a >> b){
		int x, y;
		int c = ex_gcd(a, b, x, y);
		cout << a << " * " << x << " + " << b << " * " << y << " = " << c << endl;
	}
	return 0;
}

程序输出：

4 6
4 * -1 + 6 * 1 = 2
7 9
7 * 4 + 9 * -3 = 1
6 9
6 * -1 + 9 * 1 = 3

扩展欧几里得算法的用途

求解同余式中系数的值。

例如求解如下的余式：

$$ax\%b=c$$

这里的$c$ 不一定是 $a$ 和 $b$ 的最大公约数，只要其实 $a$ 和 $b$ 最大公约数 的倍数即可。

因为根据扩展欧几里得算法，存在$x^{\prime },y^{\prime }$, 使得
$$\begin{array}{r}a{x}^{\prime }+b{y}^{\prime }=c^{\prime }\end{array}$$

其中 $c^{\prime }=gcd(a,b)$， 且$c=k^{\prime }\ast c^{\prime }$

给(4)式两边同乘 $k^{\prime }$, 即得到

$$\begin{array}{r}{k}^{\prime }{x}^{\prime }\ast a+k^{\prime }{y}^{\prime }\ast a=k^{\prime }\ast c^{\prime }=c\end{array}$$

而要求的式子 $ax\%b=c$ 可以整理成

$$ax-kb=c$$

只需令$x=k^{\prime }{x}^{\prime },k=-k^{\prime }{y}^{\prime }$，即可求得 x 的值。

即 余式
$$ax\%b=c$$ 中的$x$ 自然必定存在且可求。