近期帮一位医学朋友思考如下一个问题,如何计算一个封闭曲线与圆的相似性。在我的引导之下,最后他认为封闭曲线中的最大内切圆有研究的意义。然后百度相关问题,发现已经有比较成熟的做法,而且问题的标准概括叫做“计算轮廓内切圆”。然而,求解语言多基于c++或者基于OpenCV的代码(见文末参考网站)。这对于只用过2M语言的我来说其实理解起来有点难度,在理解众多解法的精髓上(说实话理解了个锤子。其他语言&“简洁”注释令人流泪,所以我写的这个Matlab版本注释与算法说明比较详细。当然由于全是个人的理解肯定有不妥当的地方,权作抛砖引玉),我最终造了个自认为效果还可以的程序,于是有了这篇文章(偷懒的我直接从参考网站上截取了图片,权作问题的直观描述)。

在设计最终的算法之前,我其实共设计两个大思路,具体如下:
大思路一: 沿轮廓搜索所有点集,按切线对应法线方向不断扩大半径寻找最大的内切圆。个人推测,此方法对于已知代数表达式的轮廓计算效果较好。但对于离散点集构成的轮廓具有较大不确定性。考虑到我所解决的对象基于离散轮廓为主,这种方法我没有做后续程序设计。
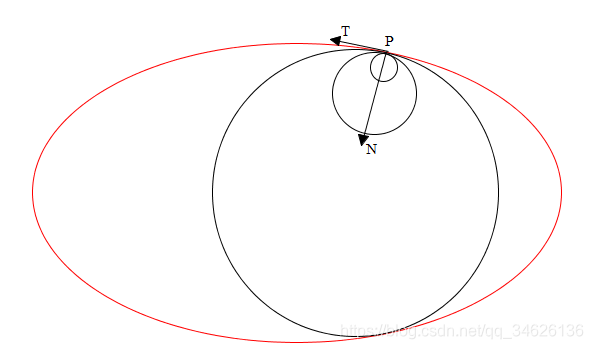
大思路二:轮廓内区域像素化,每个像素点pixel计算最大内切半径r,所有像素点对应的最大内切半径里的最大值为轮廓内切圆半径。这也是我所看到的解法中的通用思路。然后问题转化成每个像素点对应最大内切半径如何计算。
起初,在离散化轮廓内部区域后(以防强迫与恐惧症网格线间距与颜色调整得比较温柔)我考虑点到多边形的“距离”PPD(point-polygon_distance)。像素点到每条线段的距离(如果垂足不在线段上而在延长线上,则该距离视作无效),这样所有有效距离中的最小值即为待求PPD。轮廓内所有像素点对应PPD的最大值即为radius。

然而,这种判别定理对轮廓的凹凸性具有一致要求。如果凹凸相间,以上判别法则失效。

为了避免凹凸相间的轮廓,我们需要找到另一种方法计算内接圆半径radius,此时二分大法发挥了作用。初步设想如下:
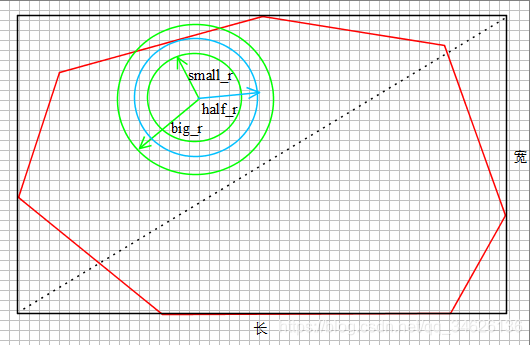
对于每个像素点,存在一个小半径(small_r)与大半径(big_r),分别使得构造的圆,不在轮廓外(含切)与部分在轮廓外。然后对半计算出半径(half_r)判断对应圆在以下情形的归属:1.不在轮廓外(含切) 2.部分在轮廓外,不断更新small_r与big_r,直到大小半径差值在精度设置precision内,最终令radius=small_r;
起初,small_r=0;注意到轮廓的内切圆半径,不会超过包含轮廓外接矩形中的最大内切圆半径,即轮廓外接矩形的长、宽较小值的一半,因此big_r=max{长,宽}/2;精度设置上可以联系外接矩形对角线长度,最终令precision=对角线长度/(2^13)。
上述算法有较大的优化空间。第一,for循环构造的像素搜索点集是矩形状的,我们可以先剔除轮廓以外的点(这也是其他语言解法的第一步)。第二,由于radius=轮廓内所有像素点对应最大圆的半径的最大值,所以像素点循环计算对应半径时,small_r可以赋值成先前计算出的radius值。如果一开始该像素以先前radius作为半径值展开,其部分圆就在轮廓之外则直接跳到下个循环,则radius维持不变。否则,继续用二分法确定的更大radius覆盖起先的radius。如此可以不断提高radius的下限以提高计算效率。第三,通常循环下,可能需要较多次数才能提升radius的下界(大概率下轮廓内切圆在靠近中间位置,靠循环搜索到哪里需要较长时间)。我们可以事先在轮廓内按比例随机选点迅速提升radius下界,使得剩余的循环中多数由于像素本身对应半径较小而直接跳过。因此最终设计的思路如下:
step1 构建外接矩形像素集并筛选出轮廓内像素集
step2 按1%随机选点利用二分法提升radius下界
step3 在剩余像素集中利用二分法计算radius
补充些许细节。Matlab自带inpolygon函数可以判断测试点集是否在离散点构成的轨迹中。因此可以将圆离散成点,程序中是分割成360个点。同时有不少计算过程重复出现且具有必要性,我特地设计一个子函数iterated_optimal_incircle_radius_get来减少代码量。接下来具体上程序与测试说明:
X,Y是轮廓的横、纵坐标向量 ,pixelx,pixely是像素横、纵坐标,small_r,big_r是确定radius上、下界,precision是精度。
function radius=iterated_optimal_incircle_radius_get(X,Y,pixelx,pixely,small_r,big_r,precision)
radius=small_r;
L=linspace(0,2*pi,360);%确定圆散点剖分数360,720
%L=2*pi*sort(rand(1,360));%随机确定圆散点剖分数360,720
circle_X=pixelx+radius*cos(L);circle_Y=pixely+radius*sin(L);
if numel(circle_X(~inpolygon(circle_X,circle_Y,X,Y)))>0%如果圆散集有在轮廓之外的点
return
else
while big_r-small_r>=precision%二分法寻找最大半径
half_r=(small_r+big_r)/2;
circle_X=pixelx+half_r*cos(L);circle_Y=pixely+half_r*sin(L);
if numel(circle_X(~inpolygon(circle_X,circle_Y,X,Y)))>0%如果圆散集有在轮廓之外的点
big_r=half_r;
else
small_r=half_r;
end
end
radius=small_r;
end
end以下是测试主程序。测试轮廓分别是心形线以及正50边形。
%Matlab 2018a
clc
clear
%构造测试轮廓
L=linspace(0,2*pi,50);
X=sin(L)-sin(2*L)/2;Y=cos(L)-cos(2*L)/2;
%X=cos(L);Y=sin(L);
%%
left_x=min(X);right_x=max(X);down_y=min(Y);up_y=max(Y);upper_r=min([right_x-left_x,up_y-down_y])/2;
%定义相切二分精度
precision=sqrt((right_x-left_x)^2+(up_y-down_y)^2)/2^13;
%构造包含轮廓的矩形的所有像素点
Nx=2^8;Ny=2^8;pixel_X=linspace(left_x,right_x,Nx);pixel_Y=linspace(down_y,up_y,Ny);
[pixel_X,pixel_Y]=ndgrid(pixel_X,pixel_Y);pixel_X=reshape(pixel_X,numel(pixel_X),1);pixel_Y=reshape(pixel_Y,numel(pixel_Y),1);
%筛选出轮廓内所有像素点
in=inpolygon(pixel_X,pixel_Y,X,Y);
pixel_X=pixel_X(in);pixel_Y=pixel_Y(in);
%plot(X,Y,'*r',pixel_X,pixel_Y,'ob')
%%
%随机搜索百分之一像素提高内切圆半径下限
N=length(pixel_X);
rand_index=randperm(N,floor(N/100));
radius=0;big_r=upper_r;center=[];
for i = rand_index
tr=iterated_optimal_incircle_radius_get(X,Y,pixel_X(i),pixel_Y(i),radius,big_r,precision);
if tr>radius
radius=tr;
center=[pixel_X(i),pixel_Y(i)];%只有半径变大才允许位置变更,否则保持之前位置不变
end
end
%%
%循环搜索剩余像素对应内切圆半径
loops_index=1:N;loops_index(rand_index)=[];
for i = loops_index
tr=iterated_optimal_incircle_radius_get(X,Y,pixel_X(i),pixel_Y(i),radius,big_r,precision);
if tr>radius
radius=tr;
center=[pixel_X(i),pixel_Y(i)];%只有半径变大才允许位置变更,否则保持之前位置不变
end
end
%%
%效果测试
circle_X=center(1)+radius*cos(linspace(0,2*pi,100));
circle_Y=center(2)+radius*sin(linspace(0,2*pi,100));
figure
hold on
axis equal
plot(X,Y,'LineWidth',2.5)
plot(circle_X,circle_Y,'LineWidth',2)
axis off
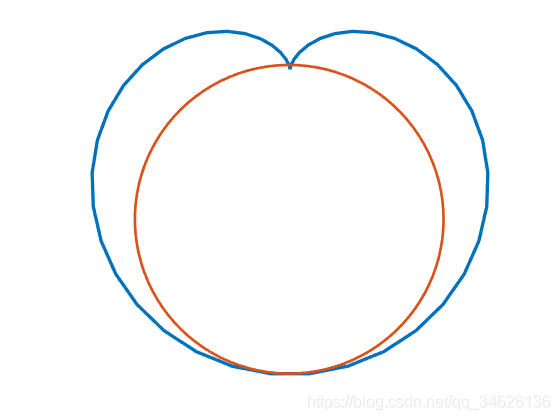
hold off在iterated_optimal_incircle_radius_get中,圆散点剖分数越大,最终效果就越精准。这在以下两张测试图中可见一斑:


后续会围绕“提取图形轮廓并绘制内切圆”这一主题展开,测试不同轮廓下程序的效率与精度。有缘我会更新这篇博客。感兴趣的朋友可以进QQ群836204107获取更多Maple相关资源。Maple技术交互研讨群欢迎每一位志同道合朋友~

https://www.cnblogs.com/jsxyhelu/p/6830093.html
https://blog.csdn.net/Lemon_jay/article/details/89467577
**************2020/8/18更新************
一年过去,没想到当初这篇博客浏览量成为我所有博客中高的一个,很是意外也难过其他博客没有被这么浏览。那时只觉着这份工作对于Matlab玩家友好,于是趁问题解决之机一并写完也属值得。这段时间陆续收到不少回复以及私信,我发现它还有可以挖掘的部分。针对常见问题以及更深问题,我在本轮更新中予以说明。
问题1:输入的轮廓数据是否有序?
回答:需要。确切地说,按照肉眼观察所依赖的顺时针或逆时针均可。因为程序中我们将依赖Matlab自带函数inpolygon,它用来判断点集与多边形的位置关系。多变形是由各个端点连接绘制而成,这导致我们容易认为给定点集合多边形样子便足以确定,进而忽视点集中内在的顺序关系。例如我们给定一组测试数据(这将下文将重复出现)并予以随机排序,进而将原先(红色)与随机排列(绿色)的点集绘制一图如下:

相同点集,顺序一旦改变,你以为的多边形形状大变。此时凹凸相错,令人眼花缭乱。进而考虑绿色多边形内切圆如何计算,恐怕难以回答。
问题2:运行时间较久怎么破?
回答:程序运行大部分时间都耗费在inpolygon函数上,此函数计算时间跟离散点集相关。由于输入轮廓数据无法改变,我们能控制的就是内切圆周离散数量以及离散方式。iterated_optimal_incircle_radius_get中存在平均离散与随机离散两种方式,读者运行时注释掉一行则选则另一行。选择随机离散方式则剖分点数可以小些,选择平均离散方式则剖分点数可以大些。不一定要选择360,720数量剖分,如果多边形形状简单则剖分数量较小也未尝不可。剖分数量越大,则检测的轮廓线可以更加复杂,这从心形线轮廓中对比测试360与720剖分而可见一斑。
L=linspace(0,2*pi,720);%等份确定圆散点剖分数360,720
L=2*pi*sort(rand(1,720));%随机确定圆散点剖分数360,720问题3:输入轮廓同时含有内外部分,如何计算?
回答:这是个很好的问题,作为我当初忽略的部分,也是本次更新的最大动力。上文出现的程序,除了二分算法,核心便是inpolygon函数。如果它能考虑内外轮廓情况,那此处便能计算,回到对应帮助文档:
Define a square region with a square hole. Specify the vertices of the outer loop in a counterclockwise direction, and specify the vertices for the inner loop in a clockwise direction. Use NaN to separate the coordinates for the outer and inner loops.
也就是说,如果分别有外、内轮廓数据(均为行向量)outer_loopx、outer_loopy、inner_loopx、inner_loopy,在二者时针顺序相反的情况下,我们只需令
X=[outer_loopx,nan,inner_loopx];
Y=[outer_loopy,nan,inner_loopy];即可实现轮廓输入。然而在上文程序中修改X,Y的Matlab输入,运行结果却有些尴尬:

何处与直觉矛盾?何处符合程序的逻辑?
我们理解的内切圆,它至少在内外轮廓里面。在上图中,内切圆它虽然在里面,但它却同时包住了内轮廓。理想内切圆应该像下图那样被内外轮廓“夹击”!

但同时回顾原先程序:输出“包住内轮廓”的内切圆是没有问题的。因为判定依据就是内切圆周离散化点集均在轮廓线以内!它在没有内轮廓的几何条件下是成立的,但如果同时涉及内外轮廓且认定“夹击型”为合理内切圆则迅速失效。
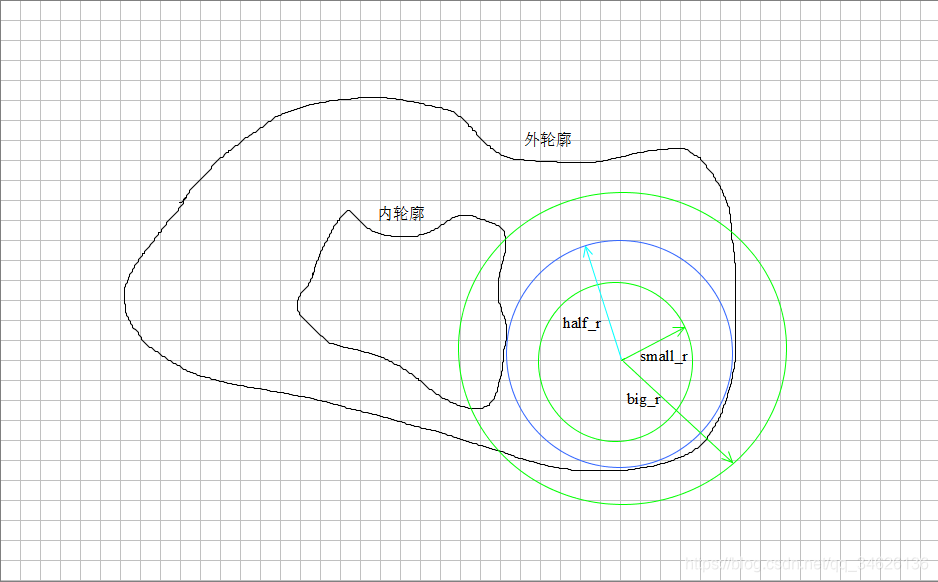
以下图为例,两条黑色曲线分别为内外轮廓。为防止内切圆包住内轮廓,在原先判定基础上,一个追加判定为“不许存在内切圆内部的点,使之位于内轮廓中”。这个新判定说起来容易实现起来却消耗原先数倍内存,这是因为之前仅考虑圆周上离散的点,如今还要考虑圆周内部离散的点。而面的离散却是线的离散上的维度级别增加。
退而求其次,我们不妨对过圆心做出数条直径并离散化,如果内切圆包住内轮廓,怎么说也有条半径穿过它,那么将存在部分离散点在内轮廓中。下图中四等分穿不过,8等分则可穿,程序中我们大力出奇迹为防不测,搞个大数等分未尝不可。
另外,考虑到面的离散计算量巨大,在程序设计时不妨引入动态数量离散机制。例如使圆盘离散的点数量随着圆盘面积的减小而指数或线性减小等。

然而,熟悉我写作风格的读者都知道,实际设计时上面思路纯粹抛转我是绝对不会去做的(嘿嘿嘿)~就刚才想法而言,语言表达起来已经有些吃力何况实际程序编写呢~我们在驻足思考一番——有没有更便捷的追加判定呢?
内切圆圆盘离散也好,多直径离散也罢,核心目的就是确保内切圆没有包住内轮廓——直接对内切圆周与内轮廓再使用一次inpolygon判断二者的几何位置关系,简单不做作!这种做法优势在于不增加新数据从而减少内存,同时仅增加部分判断较大限度保持原有程序不变。
在新函数iterated_optimal_incircle_radius_get2中,为避免数组多次拆分,将原先输入轮廓数据X,Y一开始就拆解成外、内轮廓数据outer_loopx,outer_loopy,inner_loopx,inner_loopy。
同时,在原先参数基础上增加inner_loop_num_torrence用以定义“内切圆包住内轮廓”的门槛。原本我设想一个inner_loop_num_torrence_rate,即超过这个比例的数量点位于内切圆中则认为是被包含,但后来觉得纯粹定值更为直接。inner_loop_num_torrence_rate通常随内轮廓数量增加而增加(例如一条内轮廓设为2,两条设为4),用以允许肉眼察觉不到的包含。它的值越小,则对应越苛刻的内切圆。我个人不建议直接定为0。
尽管新函数与旧函数差别不大且可以归并到一个函数中(利用if语句),但其中意义不大。
function radius=iterated_optimal_incircle_radius_get2(outer_loopx,outer_loopy,inner_loopx,inner_loopy,pixelx,pixely,small_r,big_r,precision,inner_loop_num_torrence)
radius=small_r;
X=[outer_loopx,nan,inner_loopx];Y=[outer_loopy,nan,inner_loopy];
%inner_loop_num_torrence=floor(length(inner_loopx)*inner_loop_num_torrence_rate);
L=linspace(0,2*pi,720);%等份确定圆散点剖分数360,720
%L=2*pi*sort(rand(1,720));%随机确定圆散点剖分数360,720
circle_X=pixelx+radius*cos(L);circle_Y=pixely+radius*sin(L);
if sum(~inpolygon(circle_X,circle_Y,X,Y))>0||sum(inpolygon(inner_loopx,inner_loopy,circle_X,circle_Y))>=inner_loop_num_torrence
%如果圆散集有在轮廓之外的点或者内轮廓含有超出阈值数量的在圆散集里面的点
return
else
while big_r-small_r>=precision%二分法寻找最大半径
half_r=(small_r+big_r)/2;
circle_X=pixelx+half_r*cos(L);circle_Y=pixely+half_r*sin(L);
if sum(~inpolygon(circle_X,circle_Y,X,Y))>0||sum(inpolygon(inner_loopx,inner_loopy,circle_X,circle_Y))>=inner_loop_num_torrence
%如果圆散集有在轮廓之外的点或者内轮廓含有超出阈值数量的在圆散集里面的点
big_r=half_r;
else
small_r=half_r;
end
end
radius=small_r;
end
end增加的判定1为:
%原先判定0 如果圆散集有在轮廓之外的点
sum(~inpolygon(circle_X,circle_Y,X,Y))>0
%判定1 如果内轮廓含有超出阈值数量的在圆散集里面的点。留容错
sum(inpolygon(inner_loopx,inner_loopy,circle_X,circle_Y))>=inner_loop_num_torrence
于是写出最终程序如下,采用“构造含外心形、内多变形的测试轮廓”即为上文“夹击型内切圆测试”图。
%Matlab 2019a
clc
clear
% %构造含外心形、内多变形的测试轮廓
% inner_loop_num_torrence=2;
% outer_loopx=[0,0.00104986972975232,0.00829580790753842,0.0274257295776309,0.0631461705012648,0.118776603972886,0.195939442503142,0.294367526377118,0.411843109818846,0.544273624478155,0.685900402431386,0.829627674402639,0.967451106210331,1.09095842729988,1.19186978174060,1.26258261970365,1.29668543367148,1.28940646562184,1.23796755354991,1.14181928701501,1.00274121271846,0.824799480351573,0.614163483269230,0.378792131141060,0.128008800822967,-0.128008800822966,-0.378792131141059,-0.614163483269229,-0.824799480351573,-1.00274121271845,-1.14181928701501,-1.23796755354991,-1.28940646562184,-1.29668543367148,-1.26258261970365,-1.19186978174060,-1.09095842729988,-0.967451106210332,-0.829627674402641,-0.685900402431387,-0.544273624478155,-0.411843109818847,-0.294367526377118,-0.195939442503143,-0.118776603972886,-0.0631461705012648,-0.0274257295776310,-0.00829580790753848,-0.00104986972975235,0];
% outer_loopy=[0.500000000000000,0.508142582303731,0.531635510977335,0.567742082297158,0.612122419968127,0.659149828552440,0.702323561311900,0.734750268836891,0.749661713430943,0.740933788253052,0.703571639076953,0.634127768538714,0.531024273946824,0.394756552587851,0.227963499994895,0.0353579247632598,-0.176479960179750,-0.399434132911516,-0.624289377307476,-0.841245905885823,-1.04047977645304,-1.21271376883179,-1.34976255794465,-1.44501753566408,-1.49384039966196,-1.49384039966196,-1.44501753566408,-1.34976255794465,-1.21271376883179,-1.04047977645304,-0.841245905885825,-0.624289377307477,-0.399434132911517,-0.176479960179751,0.0353579247632601,0.227963499994895,0.394756552587851,0.531024273946823,0.634127768538713,0.703571639076953,0.740933788253052,0.749661713430943,0.734750268836891,0.702323561311900,0.659149828552441,0.612122419968127,0.567742082297158,0.531635510977335,0.508142582303732,0.500000000000000];
% inner_loopx=[0.253348180407910,0.229091257656575,0.169010900017312,0.149040949964839,0.0929509812145570,-0.125211346155023,-0.250176558404032,-0.277982603466637,-0.298768902532658,-0.293154786436949,-0.255272548163554,-0.142433077522140,-0.00243963679691455,0.0354563607329167,0.0745394665669351,0.137176754525142,0.150272959269819,0.194088731581603,0.224134791812002,0.299392790375486,0.253348180407910];
% inner_loopy=[0.160669535021426,0.193693561238697,0.247861484856640,0.260358973791146,0.285236945522930,0.272620833382277,0.165564759611198,0.112808121028189,-0.0271503753092123,-0.0637202572900246,-0.157594181853538,-0.264031851161128,-0.299990080123159,-0.297897375758125,-0.290592270929419,-0.266800558503818,-0.259649836726872,-0.228756561158461,-0.199408111919728,-0.0190776589543943,0.160669535021426];
% %随机构造测试轮廓1
% inner_loop_num_torrence=2;
% % 外轮廓L1逆时针,内轮廓L2顺时针
% L1=sort(rand(1,50))*2*pi;L2=sort(rand(1,20),'descend')*2*pi;
%
% %外轮廓L1顺时针,内轮廓L2逆时针。保持内外轮廓数据呈相反时针顺序即可
% % L1=sort(rand(1,50),'descend')*2*pi;L2=sort(rand(1,20))*2*pi;
%
% %内外轮廓均为逆时针
% %L1=sort(rand(1,50))*2*pi;L2=sort(rand(1,20))*2*pi;
%
% r1=2;r2=1;
% outer_loopx=r1*cos([L1,L1(1)]);outer_loopy=r1*sin([L1,L1(1)]);
% inner_loopx=r2*cos([L2,L2(1)]);inner_loopy=r2*sin([L2,L2(1)]);
%随机构造测试轮廓2
inner_loop_num_torrence=4;
% 外轮廓L1逆时针,内轮廓L2、L3顺时针
L1=sort(rand(1,50))*2*pi;L2=sort(rand(1,20),'descend')*2*pi;L3=sort(rand(1,30),'descend')*2*pi;
r1=4;r2=1;r3=0.8;
outer_loopx=r1*cos([L1,L1(1)]);outer_loopy=r1*sin([L1,L1(1)]);
inner_loopx=[-0.7+r2*cos([L2,L2(1)]),nan,1.07+r3*cos([L3,L3(1)])];
inner_loopy=[0.7+r2*sin([L2,L2(1)]),nan,0.46+r3*sin([L3,L3(1)])];
%%
p1=randperm(numel(outer_loopx)-1);p2=randperm(numel(inner_loopx)-1);%最后一个数据同第一个形成闭环
figure
hold on
axis equal
plot(outer_loopx,outer_loopy,'-ro',inner_loopx,inner_loopy,'-ro')
plot(outer_loopx([p1,p1(1)]),outer_loopy([p1,p1(1)]),'-go',inner_loopx([p2,p2(1)]),inner_loopy([p2,p2(1)]),'-go')
axis off
hold off
%%
%轮廓合并
X=[outer_loopx,nan,inner_loopx];Y=[outer_loopy,nan,inner_loopy];
left_x=min(X);right_x=max(X);down_y=min(Y);up_y=max(Y);upper_r=min([right_x-left_x,up_y-down_y])/2;
%定义相切二分精度
precision=sqrt((right_x-left_x)^2+(up_y-down_y)^2)/2^13;
%构造包含轮廓的矩形的所有像素点
Nx=2^8;Ny=2^8;pixel_X=linspace(left_x,right_x,Nx);pixel_Y=linspace(down_y,up_y,Ny);
[pixel_X,pixel_Y]=ndgrid(pixel_X,pixel_Y);pixel_X=reshape(pixel_X,numel(pixel_X),1);pixel_Y=reshape(pixel_Y,numel(pixel_Y),1);
%筛选出轮廓内所有像素点
in=inpolygon(pixel_X,pixel_Y,X,Y);
pixel_X=pixel_X(in);pixel_Y=pixel_Y(in);
figure
plot(X,Y,'*r',pixel_X,pixel_Y,'ob')
%%
%随机搜索百分之一像素提高内切圆半径下限
N=length(pixel_X);
rand_index=randperm(N,floor(N/100));
radius=0;big_r=upper_r;center=[];
for i = rand_index
tr=iterated_optimal_incircle_radius_get2(outer_loopx,outer_loopy,inner_loopx,inner_loopy,pixel_X(i),pixel_Y(i),radius,big_r,precision,inner_loop_num_torrence);
if tr>radius
radius=tr;
center=[pixel_X(i),pixel_Y(i)];%只有半径变大才允许位置变更,否则保持之前位置不变
end
end
%%
%循环搜索剩余像素对应内切圆半径
loops_index=1:N;loops_index(rand_index)=[];
for i = loops_index
tr=iterated_optimal_incircle_radius_get2(outer_loopx,outer_loopy,inner_loopx,inner_loopy,pixel_X(i),pixel_Y(i),radius,big_r,precision,inner_loop_num_torrence);
if tr>radius
radius=tr;
center=[pixel_X(i),pixel_Y(i)];%只有半径变大才允许位置变更,否则保持之前位置不变
end
end
%%
%效果测试
circle_X=center(1)+radius*cos(linspace(0,2*pi,100));
circle_Y=center(2)+radius*sin(linspace(0,2*pi,100));
figure
hold on
axis equal
plot(X,Y,'LineWidth',2.5)
plot(circle_X,circle_Y,'LineWidth',2)
axis off
hold off作随机内外轮廓测试时,切记二者数据顺序相反——即外轮廓逆时针、内轮廓顺时针或者外轮廓顺时针、内轮廓逆时针!如果忽视这点将内外轮廓数据均作为顺时针或逆时针输入,则最终仍会出现内切圆包住内轮廓情形!



另外,我发现一位博主用Python翻译了之前的程序,很是惊讶与欣喜。如果有人对Python感兴趣的可以参照:
https://blog.csdn.net/qq_26751117/article/details/105600003























 2717
2717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








