牛顿法的图形和理论说明

牛顿法

一、图形解释牛顿法过程

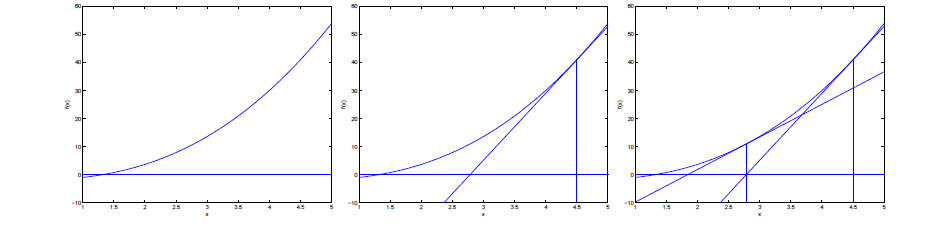
1. 在函数 f(x) 上任取一点A，作函数在A点的切线，交 X 轴于B点
2. 过B点作关于X轴的垂线交函数图像于C点
3. 再过C点作函数的切线，交X轴于D点
4. 如此重复，逼近函数 f(x) 交x轴的0点

$$设A点坐标为({\theta }_0,f({\theta }_0)),B点坐标为({\theta }_1,f({\theta }_1))...以此类推，则有：$$

$$过A点直线于x轴的夹角为：f^{\prime }({\theta }_0)=\frac{f({\theta }_0)}{{\theta }_0-{\theta }_1}$$

$$\therefore {\theta }_1={\theta }_0-\frac{f({\theta }_0)}{f^{\prime }({\theta }_0)}$$

$$...$$

$${\theta }_t{}_{+}{}_1={\theta }_t-\frac{f({\theta }_t)}{f^{\prime }({\theta }_t)}$$

$$收敛：当{\theta }_t{}_{+}{}_1={\theta }_t收敛，此时f({\theta }_t{}_{+}{}_1)=f({\theta }_t)$$

$$求f^{\prime }(x)的零点：$$

$${\theta }_t{}_{+}{}_1={\theta }_t-\frac{f^{\prime }({\theta }_t)}{f^{\prime \prime }({\theta }_t)}$$

$$收敛：当{\theta }_t{}_{+}{}_1={\theta }_t收敛，此时f’({\theta }_t{}_{+}{}_1)=f^{\prime }({\theta }_t)$$

$$求f{}^{(}{}^n{}^{)}的零点：$$

$${\theta }_t{}_{+}{}_1={\theta }_t-\frac{f{}^{(}{}^n{}^{)}({\theta }_t)}{f{}^{(}{}^n{}^{+}{}^1{}^{)}({\theta }_t)}$$

二、数学证明解释牛顿法

1. Hesse矩阵

KaTeX parse error: Undefined control sequence: \matrix at position 16: H(f) = \left[ \̲m̲a̲t̲r̲i̲x̲{ \frac{\part…

2. 泰勒公式
   $$f(x{}^k{}^{+}{}^1)=f(x^k)+f^{\prime }(x^k)(x{}^k{}^{+}{}^1-x^k)+\cdots +\frac{f{}^{(}{}^n{}^{)}(x^k)(x{}^k{}^{+}{}^1-x^k{)}^n}{n!}+\frac{f{}^{(}{}^n{}^{+}{}^1{}^{)}(\epsilon )(x{}^k{}^{+}{}^1-x^k{)}^{{}^n}{}^{+}{}^1}{(n+1)!}$$

   $$f(x{}^k{}^{+}{}^1)在x=x^k处一阶展开：$$

   $$f(x{}^k{}^{+}{}^1)=f(x^k)+f^{\prime }(x^k)(x{}^k{}^{+}{}^1-x^k)=0$$

   $$化简得：x{}^k{}^{+}{}^1=x^k-\frac{f(x^k)}{f^{\prime }(x^k)}$$

   $$f(x{}^k{}^{+}{}^1)在x=x^k处二阶展开：$$

   $$f(x{}^k{}^{+}{}^1)=f(x^k)+f^{\prime }(x^k)(x{}^k{}^{+}{}^1-x^k)+\frac{f^{\prime \prime }(x^k)(x{}^k{}^{+}{}^1-x^k{)}^2}{2!}$$

   $$令f^{\prime }(x{}^k{}^{+}{}^1)=0,对x{}^k{}^{+}{}^1求导：$$

   $$x{}^k{}^{+}{}^1=x^k-\frac{f^{\prime }(x^k)}{f^{\prime \prime }(x^k)}$$

   推广到多维：
   $$x{}^k{}^{+}{}^1=x^k-[H(f)]{}^{-}{}^1\partial f(x^k)$$

   $$S_k=-[H(f)]{}^{-}{}^1\partial f(x^k)——搜索方向$$