【二分查找】求解单调方程的解 C++实现

1 问题

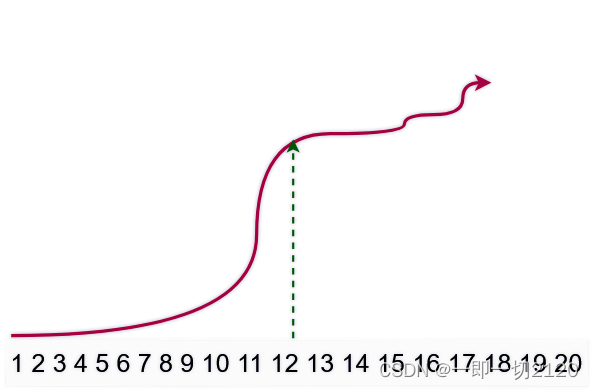
  有函数$f(x)=a^x(a>1)$ ,单调递增，现在给一个正整数$N$，求使得$f(x)=N$的正整数解$x$。
  

2 想法

1. $x=lo{g}_a^N$ 很干净利索，但这样得到的是一个浮点数，需要判断$x$是不是正整数。注意：例子特殊，并不是所有的递增函数都有直接解。
2. 从$0,1,2,3\dots \dots$开始试验，如果$a^i<N<a^{i+1}$ ,说明无解，如果$a^i=N$，那么$i$就是解。
3. 考虑单调性，从小到大去试验时，如果当前值i满足$a^i>N$，后面一定都大于$N$，说明无解。
4. 考虑边界值，注意到 $x$ 的值最小0，最大不超过N，即$x\in [0,1,\mathrm{2...},N]$，逻辑等价于数组下标，可以使用二分查找。

3 二分查找

  最常见的，一个严格单调递增有序数列，查找是否存在某一个值。可以先找中间，每次放弃一半，效率 $O(lgN)$ 。
  有两个明显特征：

1. 有明显边界且是有限个数。
2. 满足单调性。

  递归与迭代形式

function binary-search(x,A,l,r)
	if l>r then 
		not found error
	else
		m = l+floor((r-l)/2)  # (l+r)/2可能会溢出
		if A[m] = x then
			return m
		if A[m] > x then 
			return binary-search(x,A,l,m-1)
		else
			return binary-search(x,A,m+1,r)

# 递归修改边界
function binary-search(x,A,l,r)
	while(l<r)
		m = l+floor((r-l)/2)  # (l+r)/2可能会溢出
		if A[m] = x then
			return m
		if A[m] > x then 
			r=m-1
		else
			l=m+1
	return NIL

4 实现

   注意，为了一般化单调递增函数或者数列，我们把$f(x)$作为参数传入。

4-1 伪代码说明

function bisearch(f,N,l,r):	
	if l<r then
		error
	else
		m = l+floor((r-l)/2)
		y = f(m)
		if y == N then
			return m
		if y > N then
			return bisearch(f,N,l,m-1)
		else
		 	return bisearch(f,N,m+1,r)

4-2 C++11

#include <iostream>
#include <vector>
#include <functional>//function 模板
#include <cmath> //floor()

using namespace std;
#define see(x) cout << x << endl
#define see2(x, y) cout << (x) <<"\t"<< (y) << endl

class Solution
{
    using T=size_t;
    using incFunc=function<size_t(size_t)>;
public:
    static T expA(T x){
        T ans=1;
        T a=5;
        while(x--){
            ans*=a;
        }
        return ans;
    }
    T biSearch(incFunc f,T N,T l,T r){
        if(l>r){
            cerr<<"error"<<endl;
            return 0;
        }else{
            T m=l+floor((r-l)/2);
            T y=f(m);
            if(y ==N) return m;
            if(y > N) return biSearch(f,N,l,m-1);
            else return biSearch(f,N,m+1,r);
        }
    }
    void test()
    {
        T ans=biSearch(expA,125,0,125);
        if(ans==3){
            see("accept!!!");
        }else{
            see("error....");
        }
    }      
};

int main()
{
    Solution sol;
    sol.test();
    return 0;
}