金融--资产组合优化原理与实例 Portfolio Optimization

来源：http://blog.csdn.net/matrix_laboratory/article/details/50821455

1. Markowitz投资组合理论

Markowitz投资组合理论是投资组合优化的理论基础。 
马克维茨被公认为是现代投资组合理论的开创者，他与夏普、米勒共同获得1952年的诺贝尔经济学奖。 
1952年他在自己著名的论文《资产选择：有效的多样化》中首先提出了投资组合理论。马克维茨的理论主要包括“均值方差分析理论”和“有效边界模型”，他用期望收益率表示收益，用方差表示风险。该理论证明了“通过证券组合只能消除非系统风险，而不能消除系统性风险”。

---

2. 投资组合优化的目标

（1）降低风险 
（2）在等风险的情况下，通过调整投资组合以获取更高收益

---

3. 如何进行投资组合优化

这里就需要用到Markowitz投资组合理论。 
均值方差分析理论解释了为什么要建立投资组合 
有效边界模型理论解释了如何进行投资组合优化

3.1 均值方差分析理论

期望收益率表示收益，用方差表示风险。 
用前文的那个极端例子：

有n个不相关的资产，其收益率都是r，风险都是v，优化后的投资比例应该是均分

也就是说通过分散投资降低方差即投资风险。 
以期望收益E来衡量证券收益，以收益的方差 δ2 表示投资风险 
　　 minδ2(rp)=∑∑wiwjcov(ri,rj)

　　 E(rp)=∑wiri

　　式中： 
　　 rp ——组合收益；

　　 ri 、 rj ——第i种、第j种资产的收益；

　　 wi 、 wj ——资产i和资产j在组合中的权重；

　　 δ2(rp) ——组合收益的方差即组合的总体风险；

　　 cov(r,rj) ——两种资产之间的协方差。 
　

3.2 有效边界模型

通过下面的公式： 
　　

minδ2(rp)=∑∑wiwjcov(ri,rj)

　　

E(rp)=∑wiri

我们可以得到 minδ2(rp)和 E(r_p)的相关的一个公式，并且该公式存在极值点。

3.3 2项资产的投资组合优化

资产	A	B
投资比例	x1	x2
回报率	r1	r2
风险	δ1	δ2
协方差	ρ

　　 
回报率： 
　　

r=x1r1+x2r2

风险： 
　　

δ2=x21δ22+x22δ22+2x1x2ρ

令投资总数为为单位1: 
　　 r=x1r1+(1−x1)r2  …………(1)

　　 x1=r−r2r1−r2  ……………………(2)

　　 var=x21δ22+(1−x1)2δ22+2x1x2ρ  …………(3)

将（2）代入（3）

　　 δ2=(r−r2r1−r2)2δ22+(r−r1r2−r1)2δ22+2x1x2ρ …………(4)

最后我们的到了 δ2 和r的关系公式：公式（4），并且从（4）可以看出该公式是一个一元二次公式。 

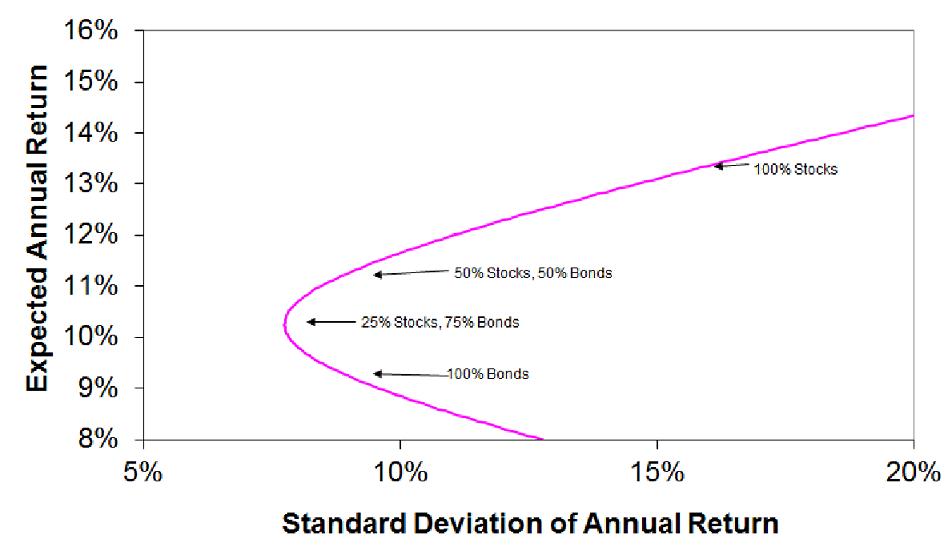
如图中曲线即为我们需要的投资边界（Efficient Portfolio Frontier），该曲线右边是我们可以采用的投资组合，曲线左边是在该投资模型下不可能取得的投资组合。 
只有在该曲线上的投资组合才是最优投资组合。

3.3 3项资产的投资组合优化与切线模型

（1）3项资产的投资组合 
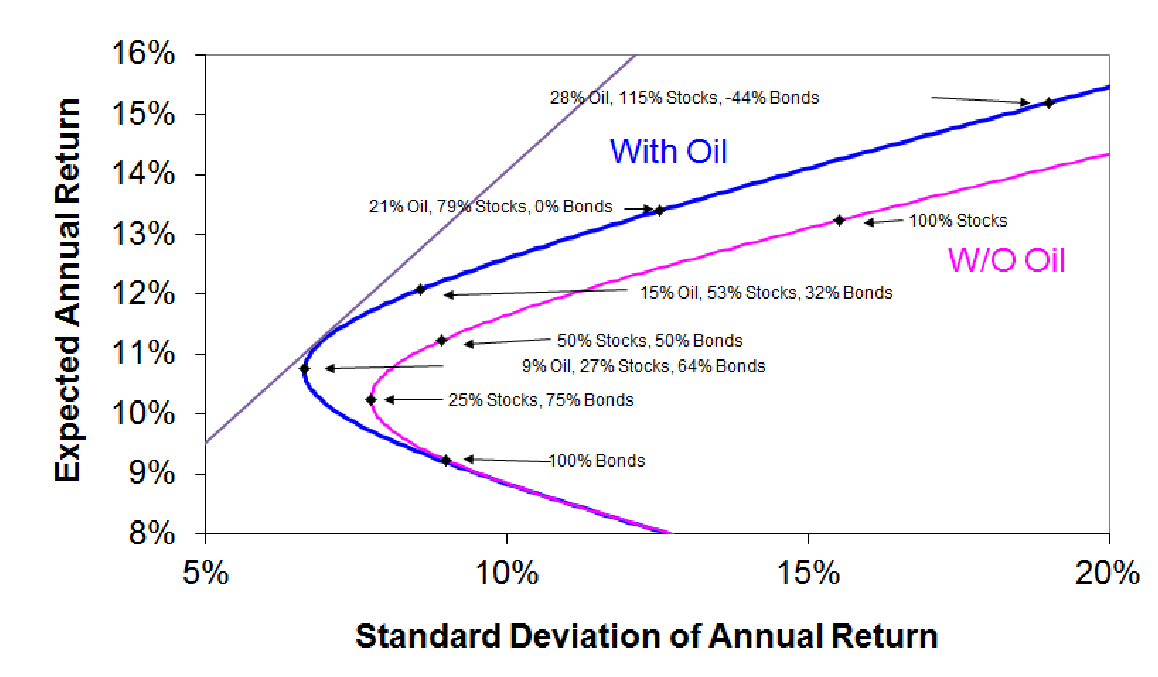
在引入一项投资资产(石油)：

从图中可以看出引入石油后的曲线（蓝色曲线）要优于未引入石油的曲线（粉色曲线）

（2）切线模型 
然后引入一种无风险资产，视该资产的风险为零，收益（ rf ）固定。 
如此可以一条直线并与未引入无风险资产的曲线相切。 
该切线组合极为最优组合，是一般投资经理应该选择的投资组合。 
切线斜率： 

ratio=r−rfδ