投资组合：投资组合优化和现代投资组合理论

etafer

已于 2024-04-25 14:20:31 修改

阅读量181

点赞数

分类专栏：投资组合文章标签：算法金融 python

于 2024-04-22 22:20:45 首次发布

原文链接：https://financialnoob.me/introduction-to-portfolio-optimization-and-modern-portfolio-theory/

版权

投资组合专栏收录该内容

3 篇文章 0 订阅

订阅专栏

投资组合：投资组合优化和现代投资组合理论

github仓库地址：https://github.com/financialnoob/portfolio_optimization

原文链接：https://financialnoob.me/introduction-to-portfolio-optimization-and-modern-portfolio-theory/

系列文章

前言

投资组合优化是量化金融的一个重要领域。它由哈里·马科维茨（Harry Markowitz）在1952年的论文《投资组合选择》中首次介绍，并进一步发展成为一个完整的研究领域。现在，存在许多不同的投资组合优化框架，几乎每天都有关于该主题的新论文发表。
投资组合优化的主要目标在其最简单的形式上是创建在给定风险水平下最大化（预期）回报的投资组合。以下是维基百科上的广义定义：

投资组合优化是从所有被考虑的投资组合集中选择最佳投资组合（资产分配）的过程，根据某些目标。这些目标通常是最大化因素如预期回报，并最小化成本如财务风险。被考虑的因素可能范围从有形的（如资产、负债、收益或其他基本面）到无形的（如选择性撤资）。

投资组合优化技术不仅可以应用于不同的资产，还可以应用于交易策略。例如，如果我们有几种不同风险的交易策略，我们可以使用投资组合优化技术来确定如何在它们之间分配我们的资本，以最大化预期回报或最小化风险。
在这篇文章中，我将描述由马科维茨在他1952年的论文中引入的现代投资组合理论（MPT）。我将展示如何在Python中实现它，以及如何使用它来构建一个简单的交易策略。在未来的文章中，我计划探索其他投资组合优化技术。

现代投资组合理论MPT

首先让我从原始论文中描述MPT背后的推理。考虑了几种可能的投资组合构建规则：

假设投资者只关心最大化预期回报。如果是这种情况，那么他们将把所有的钱投资在预期回报最高的一种工具上。鉴于市场是不完美的，未来是不确定的，显然这种方法不是最优的。
另一种方法是假设我们需要拥有一个多元化的投资组合。一些投资者可能会认为，由于大数定律（LLN），多元化投资组合的实际回报将等于预期回报。这种推理的问题在于，LLN仅适用于独立同分布（iid）的随机变量，而资产回报显然是相互依赖和互相关联的。

大数定律（Law of Large Numbers, LLN）是概率论中的一个基本定理，它描述了当进行大量独立且同分布的随机试验时，试验结果的平均值将趋近于期望值。

由此可见，我们无法通过多元化完全消除所有风险。我们能做的是在给定风险水平的情况下最大化预期回报（或在给定回报的情况下最小化风险）。这被称为均值-方差优化。

现在让我们从数学上陈述这个投资组合优化问题，然后我将展示它在实践中是如何工作的。假设我们有N种资产，预期回报为mu，协方差矩阵为sigma。我们想通过选择投资组合权重w来构建一个投资组合。
在这里插入图片描述

公式

投资组合的预期回报和方差可以按以下方式计算：
在这里插入图片描述

投资组合的预期回报和方差

一般来说，我们会关注解决两个问题。第一个是寻找最小方差投资组合。在这种情况下，我们只需要找到最小化投资组合方差σ的投资组合权重w。由于每个权重w_i代表在资产i中投资的投资组合比例，我们增加了一个约束，即所有权重的总和等于1。
在这里插入图片描述

寻找最小方差投资组合

我们通常解决的另一个问题是在给定风险（方差）水平下最大化投资组合回报。
在这里插入图片描述
这两个问题都可以通过分析方法（使用拉格朗日乘数）解决，但我不打算描述如何做到这一点。对我们来说，使用Python数值解决这些问题会更容易。

投资组合权重

我将从仅四种资产开始：AAPL, BRK.B, MMM, GLD。时间段将从2018年01月01日到2022年12月31日。以下显示了下载数据的代码。

import yfinance as yf
stocks = ['AAPL', 'BRK-B', 'MMM', 'GLD']
tmpdf = yf.download(stocks[0], start='2018-01-01', end='2022-12-31')
prices = pd.DataFrame(index=tmpdf.index, columns=stocks)
prices[stocks[0]] = tmpdf['Adj Close']
for stock in stocks[1:]:
    tmpdf = yf.download(stock, start='2018-01-01', end='2022-12-31')
    prices[stock] = tmpdf['Adj Close']

returns = prices.pct_change().dropna() # 计算回报

首先，让我们尝试使用全部历史数据来了解投资组合优化是如何工作的。看一下下面的相关性矩阵。我们可以看到，大多数资产确实与彼此高度相关。
在这里插入图片描述

相关性矩阵

解决我们问题的一种方法是使用某种蒙特卡罗方法。我们可以生成一些随机的投资组合权重，然后计算结果投资组合的回报和波动性。让我们试一试。

portfolios = pd.DataFrame(columns=list(stocks)+['return', 'sd'])

for i in range(10000):
    np.random.seed(i)
    weights = np.random.uniform(size=len(stocks)) # 生成随机权重
    weights /= weights.sum() # 使权重总和为1
    ret = weights.T @ returns.mean() * 252 # 年化回报
    sd = np.sqrt(weights.T @ returns.cov() @ weights * 252) # 年化标准差
    portfolios.loc[i] = list(weights) + [ret, sd]

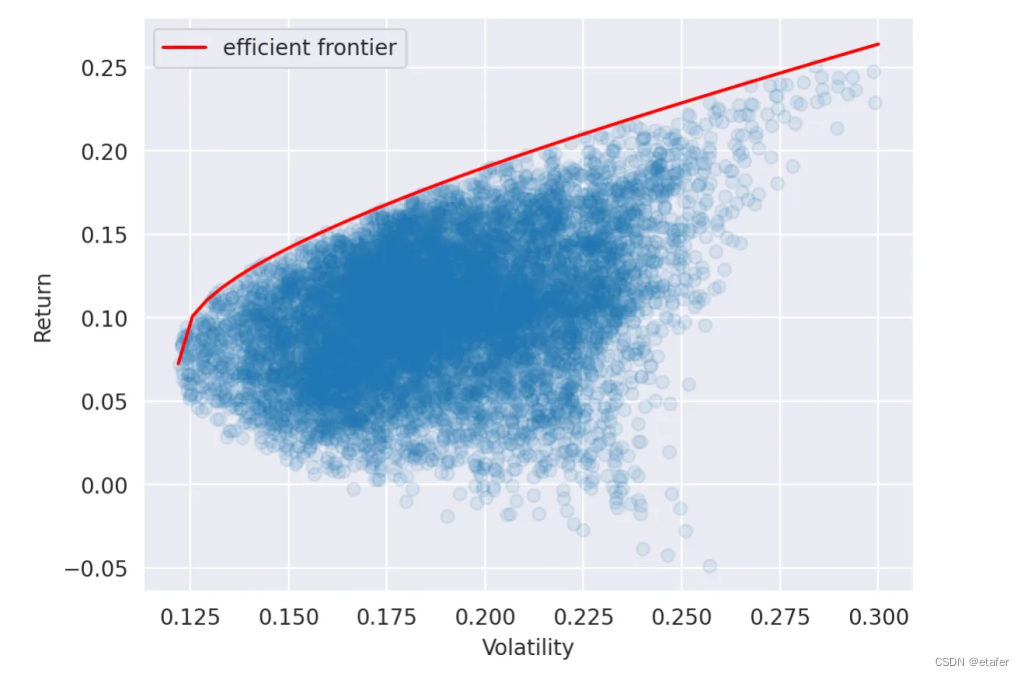
下面您可以看到那些随机投资组合的回报和波动性的图。每个点代表一个投资组合。这个图的上边缘被称为有效边界。它代表了对于给定波动性水平可以实现的最大回报。我们可以看到，随着波动性的增加，最大回报也在增加。我们还可以注意到，我们可以实现的最小波动性大约是12%。
在这里插入图片描述

随机投资组合的回报与波动性

现在我们可以使用生成的投资组合来解决前面提到的两个问题。我们可以按照以下方式找到最小方差投资组合：

在这里插入图片描述

最小方差投资组合

或者我们可以为给定水平的风险（比如说20%）找到最大回报的投资组合：

在这里插入图片描述

最小方差投资组合

现在让我们比较一下投资组合和单个资产。

在这里插入图片描述

投资组合vs单个资产

AAPL是一个异常值，我们没有投资组合能达到相同水平的回报。让我们看看BRK-B。它的回报约为10%，其波动性约为23%。但如果我们看一下随机投资组合，我们可以看到在相同风险水平下我们可以实现更好的回报 — 大约20%（是BRK-B回报的两倍多）。这就是拥有多元化投资组合的主要优势。
用生成随机投资组合的方法来解决投资组合优化问题只有在资产数量较少时才行得通。我们需要生成的随机投资组合数量随着资产数量的增加而呈指数增长。这就是为什么我们需要找到不同的解决方案。我将使用Python中scipy库的数值方法。
让我们从找到最小方差投资组合开始。我们需要定义一个我们希望最小化的函数和任何我们想要使用的约束条件。以下展示了这样做的代码。

from scipy.optimize import minimize

# 要最小化的函数
def volatility(weights, returns):
    return np.sqrt(weights.T @ returns.cov() @ weights * 252)

constraints = ({'type':'eq', 'fun': lambda x: np.sum(x)-1})

函数的第一个参数必须是我们试图找到的变量。在它之后我们可以根据需要指定任何额外的参数。
在这个问题中我们只有一个约束：投资组合权重的总和必须等于1。我在这里使用的约束类型要求我们将其指定为一个函数，如果约束满足则返回0。
接下来我们需要定义初始猜测x0和每个变量的边界。我使用相等的权重作为初始猜测。边界定义为每个资产的权重在0和1之间（目前我们只考虑多头头寸）。
在这里插入图片描述

定义初始猜测和边界

最小化操作只需一行代码即可完成。结果如下所示。
在这里插入图片描述

最小化方差投资组合的解

我们能实现的最小方差大约为12.2%，权重为x。让我们将这个解决方案与我们使用蒙特卡罗方法（随机投资组合）得到的解决方案进行比较。

在这里插入图片描述
如您所见，我们使用两种方法得到的权重是接近的。
现在让我们解决另一个问题 —— 在给定风险水平下最大化回报。最大化回报与最小化负回报相同。下面我们定义一个要最小化的函数，我们还增加了另一个约束 —— 投资组合波动性必须等于一些预定义的值。

target_vol = 0.2

constraints = ({'type':'eq', 'fun': lambda x: volatility(x,returns)-target_vol}, 
               {'type':'eq', 'fun': lambda x: np.sum(x)-1})

def negative_annual_return(weights, returns):
    ret = weights.T @ returns.mean() * 252
    return -ret

我们的边界和初始猜测保持不变。解决问题后，我们得到以下结果：

在这里插入图片描述

给定风险水平下的最大回报

对于20%的波动性，我们能实现的最大投资组合回报是19%。

注意，我们可以根据我们的需要轻松改变上面使用的约束和目标函数。例如，我们可以改变目标函数来选择一个拥有最高夏普比率的投资组合。或者修改权重的约束以允许做空。

现在让我们绘制有效边界。我们只需要找出在给定范围内一系列波动性的最大回报，然后绘制结果。

vols = np.linspace(0.122, 0.3)
rets = []

for target_vol in vols:
    res = minimize(negative_annual_return, x0, args=(returns), 
               bounds=bounds, constraints=constraints)
    rets.append(-res.fun)

plt.scatter(portfolios['sd'], portfolios['return'], alpha=0.1)
plt.xlabel('Volatility')
plt.ylabel('Return')
plt.plot(vols, rets, color='r', label='efficient frontier')
plt.legend()

在这里插入图片描述

有效边界

接下来我们可以做的事情是允许做空。通过改变边界值很容易做到这一点。现在我们希望我们的权重范围在-1到1之间。其中一个约束也需要更改。现在我们检查权重的绝对值之和是否等于1。其余的操作相同。

constraints = ({'type':'eq', 'fun': lambda x: np.sum(np.abs(x))-1},)
bounds=[[-1,1]]*len(stocks)

首先我们找到最小方差投资组合在这里插入图片描述

最小方差投资组合的解

现在我们能够实现的最小方差是7.5%（相比之下不允许做空时是12.2%）。让我们尝试在20%的目标波动性下最大化回报。

target_vol = 0.2

constraints = ({'type':'eq', 'fun': lambda x: volatility(x,returns)-target_vol}, 
               {'type':'eq', 'fun': lambda x: np.sum(np.abs(x))-1})

在这里插入图片描述

给定风险水平下的最大回报

现在我们可以实现大约21.46%的回报（相比之下不允许做空时是18.56%）。下面我将绘制新的有效边界，并将其与之前的有效边界（不允许做空）进行比较。

vols_ss = np.linspace(0.08, 0.3)
rets_ss = []

for target_vol in vols_ss:
    res = minimize(negative_annual_return, x0, args=(returns), 
               bounds=bounds, constraints=constraints)
    rets_ss.append(-res.fun)

plt.scatter(portfolios['sd'], portfolios['return'], alpha=0.1)
plt.xlabel('Volatility')
plt.ylabel('Return')
plt.plot(vols_ss, rets_ss, color='c', label='efficient frontier (with short-selling)')
plt.plot(vols, rets, color='r', label='efficient frontier (without short-selling)')
plt.legend()

在这里插入图片描述

有效边界组合

如您所见，允许做空显著改善了有效边界 —— 我们能够在相同的风险水平获得更好的回报（或在相同回报的水平降低风险）。

回测

注意，在上面我使用所有可用数据来计算回报和协方差矩阵。基本上我们解决了一个给定历史数据集的投资组合优化问题。我们找到的投资组合适用于这个特定的历史时期，但不保证在未来也有效。这并不是很有用。实际上，我们现在想要构建一个最佳投资组合，我们希望它在未来一段时间内保持其属性（预期回报和波动性）。为了实现这一点，我们需要对未来的回报和协方差矩阵进行一些估算。
目前让我们尝试使用最简单的估算器 —— 样本均值和协方差矩阵。我将使用相同的四种资产，并尝试基于上述技术创建一个交易策略。我将使用一年的历史数据来估算预期回报和协方差矩阵，并且我将每周重新平衡我的投资组合。
执行回测的代码如下所示。一些需要注意的事项：

我试图在20%的波动性下实现最大回报。
不允许做空。
使用每日数据解决投资组合优化问题（以便有更多的数据点估算协方差矩阵）。
交易成本不包括在内。

# # 以周为单位重新采样价格数据，并获取每周的最后一个价格
prices_w = prices.resample('1W').last()
# 计算周价格变化的百分比变化，并删除任何NaN值
returns_w = prices_w.pct_change().dropna()
#创建一个空的DataFrame，其索引是从2019年1月1日开始的价格数据，列与股票名称相同
positions = pd.DataFrame(index=prices_w.loc['2019-01-01':].index, 
                         columns=prices_w.columns)

# 设定目标波动性为20%
target_vol = 0.2
# 定义约束条件，包括波动性目标和权重和为1
constraints = ({'type':'eq', 'fun': lambda x: volatility(x,returns_tmp)-target_vol}, 
               {'type':'eq', 'fun': lambda x: np.sum(x)-1})
# 为每种股票设定权重边界在0到1之间（不允许做空）
bounds=[[0,1]]*len(stocks)
# 初始化权重，平均分配
x0 = np.ones(len(stocks)) / len(stocks)

# 遍历每个周索引
for t in tqdm(returns_w.loc['2019-01-01':].index):
	# 获取当前时间点之前的最后252个交易日（大约一年）的价格
    prices_tmp = prices.loc[:t].iloc[-252:]
    # 计算这些价格的百分比变化
    returns_tmp = prices_tmp.pct_change().dropna()
    # 使用最小化函数来求解优化问题，找出最大化回报的权重
    res = minimize(negative_annual_return, x0, args=(returns_tmp), 
               bounds=bounds, constraints=constraints)
    # 将计算出的权重存储到positions DataFrame中
    positions.loc[t] = res.x
    
# 计算投资组合的累计回报，将各股票的位置偏移一位来模拟重新平衡前的状态
cumret_mpt = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
# 计算等权重投资组合的累计回报作为比较
cumret_eqw = (1 + returns_w.loc['2019-01-01':].sum(axis=1)/returns_w.shape[1]).cumprod()

现在我们来绘制结果

在这里插入图片描述

累计回报

在这里插入图片描述

表现指标

这种简单的策略表现得比等权重投资组合更好。让我们看看我们是否达到了所需的波动性水平。

在这里插入图片描述

投资组合回报的波动性

实际波动性仅略高于所需的20%值。这是一个好结果，但我相信这只是运气。如果我们尝试用不同的资产回测同样的策略，结果可能就不会这么好了。你可以很容易地自己试一试 —— 只需要更改笔记本开始部分定义的资产列表。

总结

本文介绍的MPT的基础版本有很多限制。其中一个主要的批评是它假设回报是正态分布的，这通常不是情况。另一个大问题是使用预期值来代表未来回报和协方差矩阵。我们如何估算这些值对我们所实现的结果有很大影响。这里我使用了可能是最简单的估算器 —— 样本均值和协方差矩阵，但它们通常有很高的估计误差，并导致性能差的最优投资组合。在下一篇文章中，我将尝试测试不同的估算器，并观察它们如何影响最优投资组合的性能。

Jupyter notebook及源码可在此处获取。

引用

[1] 投资组合选择 (Markowitz, 1952)

[2] 量化股票投资 (Fabozzi, 2010)

[3] https://en.wikipedia.org/wiki/Portfolio_optimization

[4] https://www.kaggle.com/code/trangthvu/efficient-frontier-optimization

[5] https://colab.research.google.com/drive/1ulDSw7DEJH1SYRVwvtJXYU0naFgaaBiR

[6] https://ocw.mit.edu/courses/18-s096-topics-in-mathematics-with-applications-in-finance-fall-2013/resources/lecture-14-portfolio-theory/

etafer

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
投资组合：投资组合优化和现代投资组合理论

本文介绍了现代投资组合理论（MPT）的基本概念，其中包括使用历史数据来优化投资组合，以在特定的风险水平下最大化预期回报。通过Python演示了如何生成随机投资组合，计算它们的预期回报和波动性，并探讨了最小方差投资组合和给定风险水平下回报最大化的策略。文章还涉及了允许和禁止做空的情况下的有效边界绘制，并通过回测验证了策略性能。尽管使用了简单的历史均值和协方差矩阵估算器，策略表现出色，但估算误差可能导致最优投资组合性能下降，并计划在后续文章中探索不同的估算器对投资组合性能的影响。
复制链接

扫一扫