机器学习之Adaboost（机器学习技法）

逐步增强法（AdaptiveBoosting）引例

逐步增强法的主要思想就是拿着一堆很弱的模型可以合成一个非常强大的模型（这一点与Bagging十分相似）。

一个案例对算法的直观描述

在课堂上老师让小孩去辨识图中那些是苹果，由于小孩的思维比较简便所以他们一次只能够学到一条规则：

 

一号同学说苹果是圆的所以他在一些图片的辨识上回犯错如下，所有的错误都放大显示所有的正确的都相对缩小：

 

这时我们的做法就是将一号同学犯错的部分放大以便引起下一个同学的注意。而下一个同学会在上一个学生的基础上提出一条新的规则（也就是在图中将苹果误判的图片中找规律）。假设下一个学生说苹果是红色的这条规则，这时判断苹果的规律就成了圆的红色的他犯的错误如下：

 

就按照这样的“放大错误缩小正确”的方式来让机器去专注于犯错的资料判断上调整下一次学习的注意事项最后达到错误率的最小化。

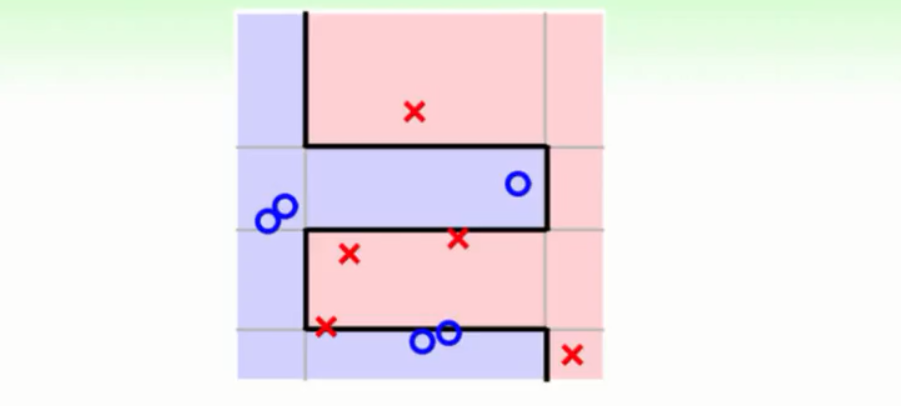
下图就是使用逐步增强法来将一些简单的模型组合起来的结果，表现的非常不错。

 

逐步增强法的一些准备

从Bagging开始

Bagging的核心在于BootStrapping，它有时会得到相同的资料如下图所示：

 

在错误衡量方面假如说一笔资料犯了错误我们就要乘上它对应的权重。比如在上图中X1犯错我们就要在它的单笔错误上乘2，而在X3犯错误时就要乘以0,因为就没有X3这笔资料。这就是我们给予不同重要的错误在计算上采用的策略，几倍重要就给予几倍的权重。也就是图中的u控制了这个权重，这些错误权重的大小就会影响到我们学习的侧重点进而得到不同的模型g。

得到不同的模型g

得到不同的模型g是我们能够通过融合过程得到好的模型的关键（各取所长）所以我们需要不同的g。现在我们试着得到两个非常不同的g如下图所示：

 

我们的gt是在ut为权重的情况下得到的，g(t+1)是在u(t+1)为错误权重的情况下得到的。他们所在乎的错误不同，比如有的在乎颜色上面的错误有的在乎形状上面的错误。如果g在u(t+1)为错误权重的情况下得到结果很差那么就说明演算法在两堆资料所在乎的错误非常不同所以在第二次学习时我们就不会学到与gt相似的模型了，进而学到的两个模型gt与g(t+1)非常不同。通过这样的策略我们得到了不同的模型g。

通过上面的解释我们就知道要想得到一个不同于当前的模型一个方法就是让我们这个模型在新的权重的资料上表现不好。表现不好就是这个模型在新的实例上的判断就像乱猜一样，而用乱猜的方式去做是非题从长远来看它的准确率就是1/2。在这个问题中数学化的表达就是犯错误的权重/总权重 = 1/2如下图所示:

 

为了让当前的模型在新的权重的资料上表现为乱猜那么就要满足上图的条件，进一步推导为正确的权重 = 错误的权重，如下图：

 

现在我们的目标就成了，拿着当前的模型在下次训练时资料的错误权重能够与正确的权重相同，这样也就达到了本次的模型在下次的资料上表现为乱猜的效果。所以我们采用的方式就是当前的做错的乘上作对权重的比例做对的乘上做错权重的比例如下图所示：

 

Adaboost算法

更有意义的放缩因子

现在我们不在使用上面的规则去更新新一轮资料的权重而是使用下图中的规则：

 

其中ε就是我们当前轮资料中错误权重的比例，我们的新的因子就是方块t（◆t）。在更新的时候我们会在犯错误权重的资料上乘上◆t，在正确的权重上除以◆t，这样就达到了让我们新的算法更注重于上一个算法犯错误的地方。具体来说，如果ε的值<=1/2那么也就是说现在模型的表现要比乱猜来的好。在这个情况下◆t会大于1这样就会使得错误被放大正确被缩小。

演算法遇到的问题

现在我们的演算法基本上为以下两个步骤：

①使用一个算法学到一个模型g

②更新我们的权重u使得我们的下一轮的训练更加集中到我们犯错误的资料上，进而得到不同的g。最后将g合起来返回G。

我们遇到了这样两个问题：

①我们的初始资料的权重没有确定

在刚开始我们还没有对资料做过任何的手脚，然后我们还想在这个资料上表现的好那么我们的做法就是每笔资料的初始权重都为1/N。

②我们该如何组合我们的模型g

如果是“每人一票”那么就会有g1对Ein很好但是g2对Ein很不好的场景，这样会使得投票的效果丧失。显然“每人一票”的方式不合理，更为合理的方式就是用线性的或者是非线性的组合方式对Ein好的模型我们给予多的票数对Ein不好的我们就会减小或者取消它的投票资格。

边学习边融合

我们先要一种一边学到g一边将g融合起来的演算法，我们尝试一种线性融合的演算法步骤如下：

 

初始条件：在所有资料权重都为1/N的情况下进行学习

①学习得到一个模型g。

②通过◆t更新权重。

③计算每个g在线性融合时的权重α。

最后返回我们的融合模型G。

现在我们的问题就集中到了α的计算上来。实务上我们的策略是α = ln(◆t)。◆t有如下的物理意义下图所示：

 

①当一个模型是乱猜的时候（错误率ε为1/2），◆t = 1，α = 0。也就是我们取消了这个模型的投票资格。

②当一个模型的准确率为100%的时候（错误率ε为0），α = ∞。也就是如果碰到一个好的算法我们要给他很多的票数。

上述的这一套算法就是著名的Adaboost演算法

 

其中演算法A就相当于一个学生，权重的调节就像是一个老师，最后将所有的模型融合在一起也就像是这个班级。最后融合的算法各取所长最后解决复杂的问题。

下图是对Adaboost算法的一个总体的概述：

 

其中Boosting的意思就是加强，也就是在刚开始我们并没有一个很好的模型g。但是只要我们有一个不是乱猜的g我们就能够能通过AdaBoost这样的演算法达到模型的增强。

AdaBoost在VC理论下的保证

 

数学上给出了一个结论就是在进行O(logN)的运算后能够使得融合模型G在训练资料上的错误率为0。当然我们的前提是有一个错误率错误率小于1/2的模型。

同时根据函数的性质判断，上式的第二项在进行O(logN)的迭代之后也会变得很小。我们的复杂度就得到了一个控制。

综上我们能够在较少的步骤中就能够得到一个很好的模型，我们只有一点点的要求就是要有一个错误率错误率小于1/2的模型作为基础。

寻找弱模型

在AdaBoost的开始我们需要一个弱的模型作为开始，事实上我们以前接触过一个比较弱的模型而且它的表现要比乱猜来的好它就是DecisionStump如下图所示：

 

它的特点是：

①只关注一个维度的特征去做判断。同时有三个参数选择哪个维度，这个模型的分界点在哪里，正负分别的方向。

②对应到二维的资料上就是这个模型只能够且竖直刀和水平刀，两种简单的边界。

③找到最佳的DecisionStump所花的时间是O(d·NlogN)。

 

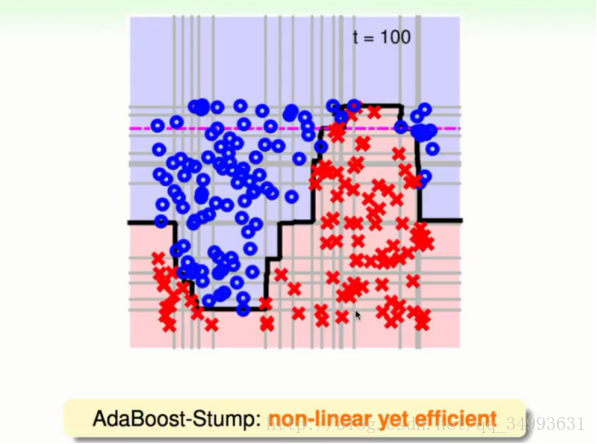
这个模型在配合Adaboost算法会得到一个非常强大的模型。甚至可以切除非常复杂的非线性曲线来。下图就是一个简单的DecisionStump配合Adaboost进行100轮之后所切割的超平面：

 

实务上Adaboost算法应用于人脸辨识的智能引用中。