数字图像处理学习笔记（五）上

第 9 章形态学图像处理

引言

形态学（morphology）一词通常表示生物学的一个分支，该分支主要研究动植物的形态和结构。将数学形态学作为工具从图像中提取表达和描绘区域形状的有用图像分量。

9.1 预备知识

集合 B 的反射表示为 $\overline{B}$， 定义如下 ：

B ‾ = { w ∣ w = − b , b ∈ B } \overline{B} =\lbrace w \mid w=-b, b\in B\rbrace B={w∣w=−b,b∈B}
形态学中集合的反射和平移广泛用来表达基于结构元（SE）的操作：研究一幅图像中感兴趣特性所用的小集合或子图像。

9.2 腐蚀和膨胀

腐蚀

作为 $Z^2$中的集合 A 和 B，表示为 AƟB 的 B 对 A 的腐蚀义为
A Ɵ B = { z ∣ ( B ) z ⊆ A } AƟB =\lbrace z \mid (B)_z \subseteq A \rbrace AƟB={z∣(B)z​⊆A}

该式指出 B 对 A 的腐蚀是一个用 z 平移的 B 包含在 A 中的所有的点 z 的集合。

膨胀

A 和 8 是$Z^2$中的集合，表示为 A$⨁B$ 的 B 对 A 的膨胀定义为:
A ⨁ B = { z ∣ ( B ^ ) z ∩ A ≠ ∅ } A\bigoplus B =\lbrace z \mid (\widehat{B})_z \cap A \not=\emptyset\rbrace A⨁B={z∣(B )z​∩A​=∅}

腐蚀是一种收缩或细化操作，膨胀则会“增长”或“粗化” 二值图像中的物体。

对偶性

膨胀和腐蚀彼此关于集合求补运算和反射运算是对偶的，即
$$\begin{gathered} （AƟB{）}^c=A^c⨁B^c \\ （A⨁B{）}^c=A^cƟB^c \end{gathered}$$

B 对 A 的腐蚀是$\hat{B}$对$A^c$的膨胀的补，反之亦然。

9.3 开操作与闭操作

膨胀会扩大一幅图像的组成部分，而腐蚀则会缩小一幅图像中的组成部分。

开操作一般会平滑物体的轮廓、断开较窄的狭颈并消除细的突出物。 闭操作同样也会平滑轮廓的一部分，但与开操作相反，它通常会弥合较窄的间断和细长的沟垫，消除小的孔洞，填补轮廓线中的断裂。

结构元 B对集合 A 的开操作，表示为 $A\circ B$ 其定义如下 ：
$$A\circ B=(AƟB)⨁B$$
用结构元 B 对集合A 的闭操作，表示为 $A\cdot B$，定义如下：
$$A\cdot B=(A⨁B)ƟB$$

开操作满足下列性质：

1. $A\circ B$ 是 A 的一个子集（子图像） 。
2. 如果 C 是 D 的一个子集，则 $C\circ B$是 $D\circ B$的一个子集。
3. $(A\circ B)\circ B$ = $A\circ B$。

闭操作满足下列性质：

1. A 是 A•B 的一个子集（子图像） 。
2. 如果 C 是 D 的一个子集，则 C•B 是 D•B 的一个子集。
3. (A•B)•B =A•B

9.4击中或击不中变换

形态学击中或击不中变换是形状检测的一个基本工具。
形态学击中或击不中变换:
$$\begin{gathered} A⨂B=(AƟD)\cap [A^cƟ(W-D)] \\ A⨂B=(AƟB_1)\cap [A^cƟB_2) \\ A⨂B=(AƟB_1)\cap [A^c⨁{\hat{B}}_2) \end{gathered}$$

9.5 一些基本的形态学算法

在处理二值图像时，形态学的主要应用之一是提取用于表示和f描述形状的图像成分。

边界提取

$\beta (A)$的集合 A 的边界可以通过先用 B 对 A 腐蚀，而后执行 A 和腐蚀的结果之间的集合之羞得到，即
$$\beta (A)=A-(AƟB)$$其中B是一个适当的结构元。

孔洞填充

一个孔洞可被定义为由前景像素相连接的边界所包围的一个背景区域。

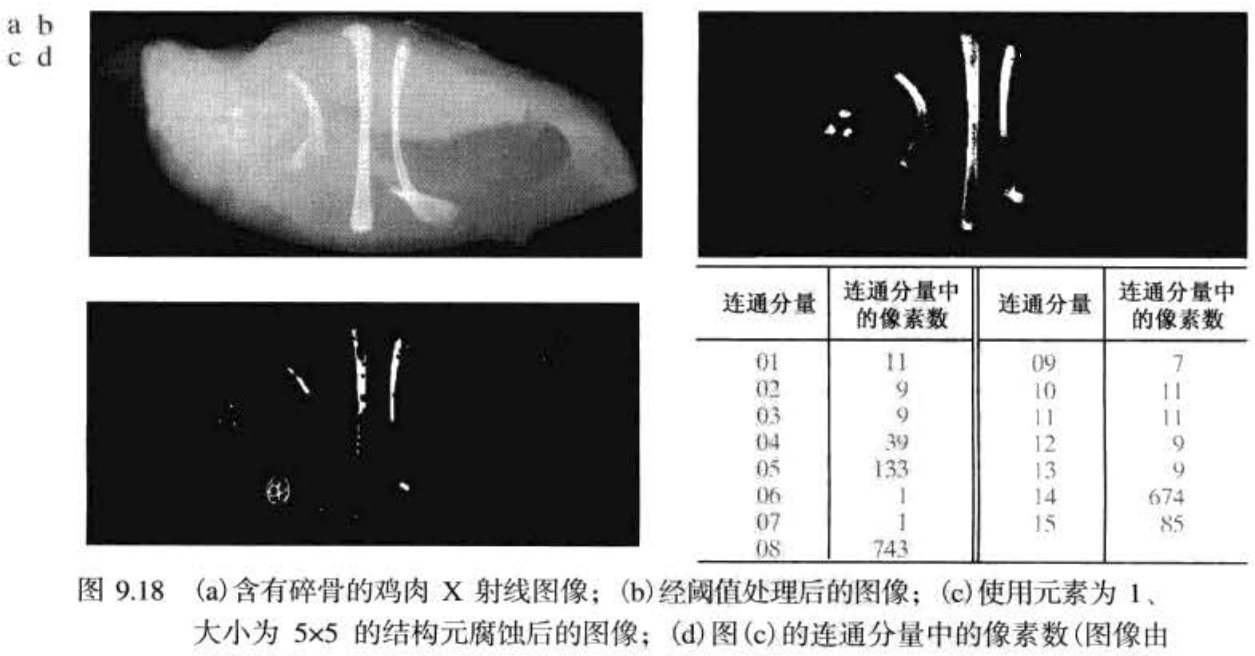
连通分量的提取

令 A 是包含一个或多个连通分量的集合，并形成一个阵列 $X_0$（该阵列的大小与包
含 A 的阵列的大小相同），除了在对应于 A 中每个连通分量中的一个点的已知的每一个位置处我们已置为 1（前景值）外，该阵列的所有其他元素均为 0（背景值） 。 如下迭代过程可完成这一目的：
$$X_k=(X_{k-1}⨁B)\cap A,k=1,2,3,\cdot \cdot$$
B 是千适当的结构元, 当 $X_k=X_{k-1}$－• 时,迭代巳过程结束。

凸壳

如果在集合 A 内连接任意两个点的直线段都在 A 的内部，则称集合 A 是凸形的。 任意集合 S 的凸壳H 是包含于 S 的最小凸集。 集合差 H-S 称为 S 的凸缺。

细化

结构元 B 对集合 A 的细化可表示为 $A⨂B$ ， 它可以根据击中或击不中变换来定义：

粗化

粗化是细化的形态学刑’偶，定义如下：
$$A\cdot B=A\bigcup (A⨂B)$$

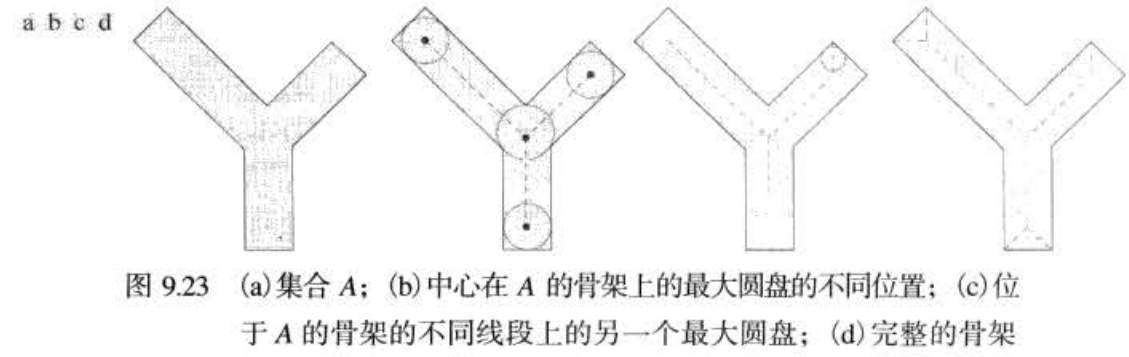
骨架

A 的骨架可以用腐蚀和开操作来表达，即骨架可以表示为
$$S(A)=\bigcup _{k=1}^K{S}_k(A)$$

裁剪

裁剪方法本质上是对细化和骨架算法的补充，因为这些过程会保留某些寄生分量，因而需要用后处理来清除这些寄生分量。

形态学重建

形态学重建的核心是测地膨胀和测地腐蚀这两个概念。

9.6小结

本章介绍了形态学概念和技术，以及从图像中提取感兴趣特征的工具。这张有点晦涩难懂，虽然是工具，但是介绍的是概念性的理论性的东西偏多。给我的感觉和第七章一样，没理解到位。后续继续找些课程加深一下理解。