人工智能入门课程学习（6）——线性回归

1.线性回归的简介

1.1 定义

线性回归(Linear regression)是利用回归方程(函数)对**一个或多个自变量(特征值)和因变量(目标值)**之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

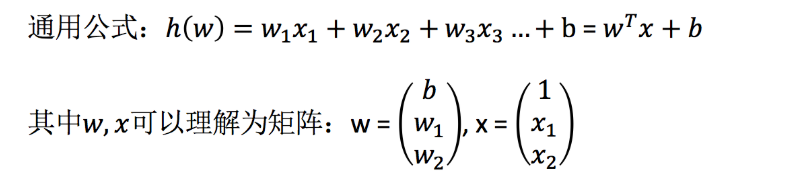
1.2 线性回归的应用场景

• 房价预测

• 销售额度预测

• 贷款额度预测

1.3 线性模型理解

举两个例子：

期末成绩：0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

使用线性回归的API解决上边的期末成绩案例

线性回归API

sklearn.linear_model.LinearRegression()
LinearRegression.coef_：回归系数

解决的数据

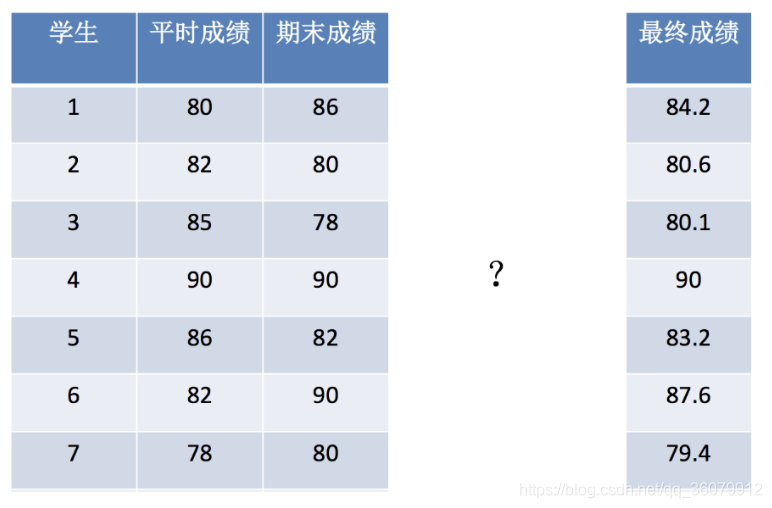
代码实现

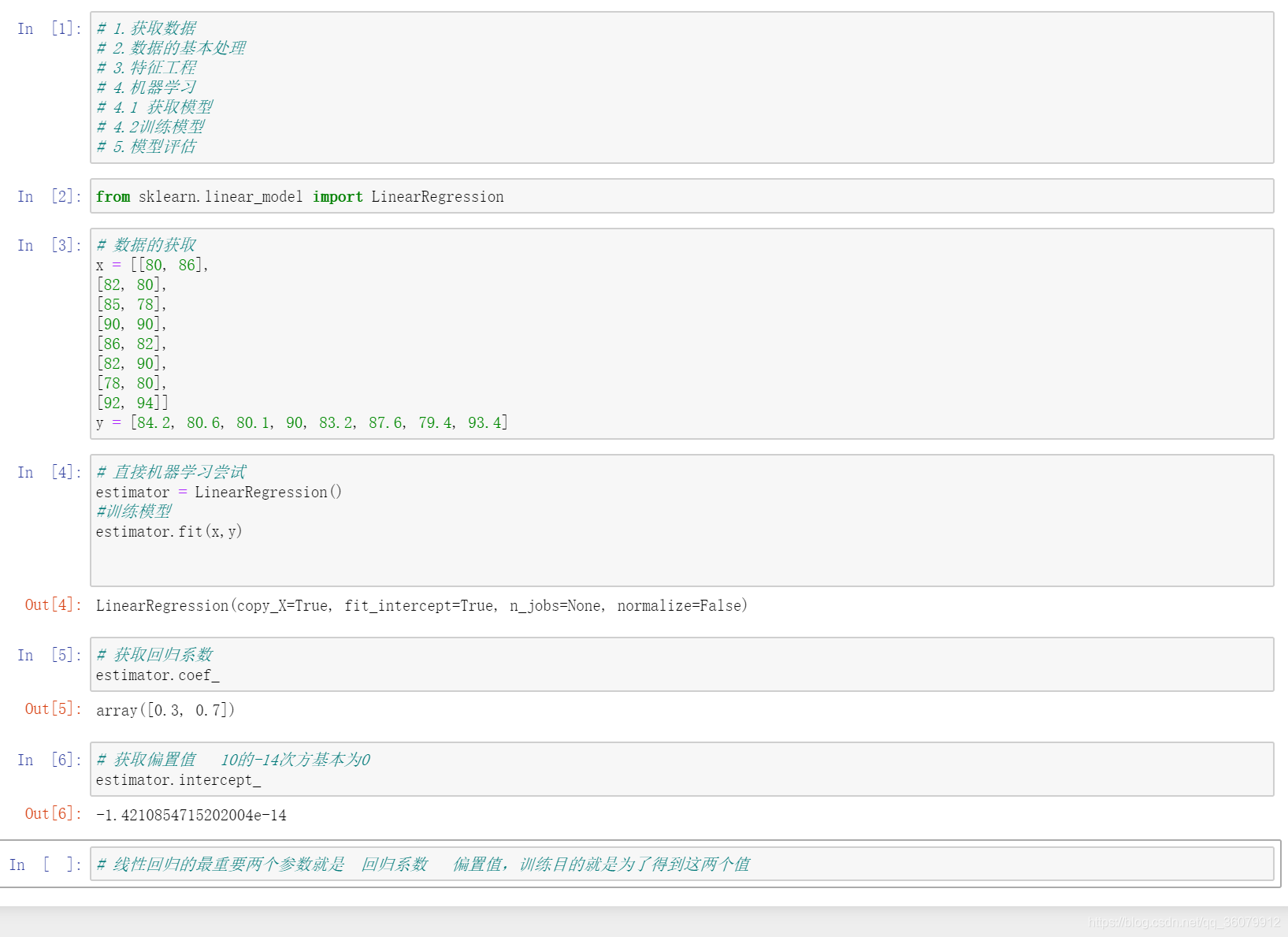
2.线性回归的损失与优化

在实际中，真实的回归系数与我们预测的回归系数可能截然不同，真实结果与预测结果之间的差值我们就用损失函数来表示。

2.1 损失函数

总损失定义为：


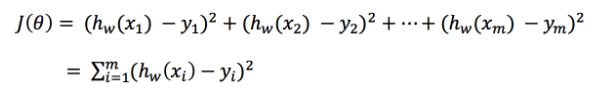
如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！
很多时候对算法的优化就是在求在J(θ)取得最小值（极小值）的时候，对应的回归系数w的值
求J(θ)的极小值的时候常常会遇到局部最优问题，如何解决局部最优问题，找到全局的最优值是机器学习中的重点。

2.2 优化方法

常用的优化方法包括正规方程法和梯度下降法。两者的对比：


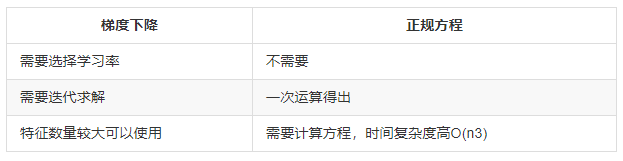
常用的梯度下降法：

• 全梯度下降算法(Full gradient descent）FG
• 随机梯度下降算法（Stochastic gradient descent）SG
• 随机平均梯度下降算法（Stochastic average gradient descent） SAG
• 小批量梯度下降算法（Mini-batch gradient descent） mini-bantch

3.scikit里边的线性回归api具体介绍

• sklearn.linear_model.LinearRegression(fit_intercept=True)
  • 通过正规方程优化
  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数
  • LinearRegression.intercept_：偏置
• sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
  • SGDRegressor类实现了随机梯度下降学习，它支持不同的 loss函数和正则化惩罚项来拟合线性回归模型。
  • loss:损失类型
    • loss=”squared_loss”: 普通最小二乘法
  • fit_intercept：是否计算偏置
  • learning_rate : string, optional
    • 学习率填充
    • ‘constant’: eta = eta0
    • ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
    • ‘invscaling’: eta = eta0 / pow(t, power_t)
      - power_t=0.25:存在父类当中
      - 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • SGDRegressor.coef_：回归系数
  • SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API， 可以根据选择使用

4. 案例：波士顿放假预测