论文阅读笔记《Morphology-Agnostic Visual Robotic Control》

核心思想

  该文提出一种在高度自由条件下的机器人视觉控制方法，该方法能够在机器人的驱动不精确、没有本体感知反馈（proprioceptive feedback）、形态学条件未知、相机姿态未知甚至是在不稳定的手持相机拍摄条件下，实现机器人的自识别和运动控制，能够在视觉引导下完成3D空间点的到达、轨迹跟踪和机器人之间动作模仿等任务。常见的机器人视觉引导控制，通常需要固定的相机位置，并对相机参数进行准确的标定，还需要知道机器人基本的形态学信息，如关节，躯干等部件的尺寸位置等。而该文提出的方法能够在上述条件完全未知的情况下，对机器人进行控制，整个过程可以分成两个阶段，第一阶段是实现机器人的自识别，也就是从相机图像中找到机器人本体所在的位置，明确控制对象点（control points）；第二阶段就是通过视觉伺服控制的方式，引导控制对象点逐步靠近目标位置，整个过程如下图所示

  首先，要先通过一段机器人运动的视频，来确定机器人的在图像中所在的位置，这个过程用到了一种称为互信息（mutual information）的方法。互信息的定义如下

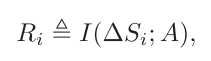
其中$R_i$表示点$P_i$的响应得分，$\Delta S_i=S_i(t+1)-S_i(t)$表示点$P_i$的位置变化，$A(t)$表示控制指令，$I(\cdot ,\cdot )$表示互信息计算方法，计算过程如下

其中$H(\cdot )$表示熵，熵值越大表示该点位置变化的不确定性越大，而$H(\cdot |\cdot )$表示条件熵，条件熵值越大表示在条件$A$已知的情况下，$\Delta S_i$的不确定性越大。上式的意思就是说，对于机器人上的点，因为他是在不断运动的，所以位置变化的不确定性很高，即$H(\Delta S_i)$的值很大，而当机器人的控制指令$A$已知时，其位置的不确定性会大幅减少，即条件熵$H(\Delta S_i|A)$很小，那么他的互信息响应值$I(\Delta S_i;A)$就很大。而对于背景中的点，其位置不会随着机器人的运动而发生改变，因此其互信息响应值应该为0。利用这一方法就能够迅速的选择出机器人上的点，并且选择其中响应值最大的$K$个点计算位置的平均值，就得到了机器人末端的控制对象点（MRCP）。
  最后就是利用视觉伺服的方法引导控制对象点MRCP去逐步靠近目标点（如图中蓝绿色点表示）。

实现过程

  在实现过程中，作者采用了一种由粗到精的控制点计算方法，首先利用Shi-Tomasi角点检测方法从图像中寻找出可能的目标点，然后分别计算这些点的互信息响应值，并选择其中最大的$K$个点作为候选点。以候选点为中心，分别计算每个候选点附近15*15范围内的点的响应值，再从中选择响应值最大的$K$个点，并计算平均值得到最终的控制对象点MRCP，如下图所示

  在计算位置变化$\Delta S_i$时需要对点进行跟踪，本文采用Lucas-Kanade光流估计方法来实现点的跟踪，对于跟踪过程中丢失的点，本文在计算MRCP时会将其丢弃，只计算整个过程都完整跟踪的目标点。因为控制对象是一个刚性的机械臂，这可能导致大部分目标点计算得到的响应值都相同，为了打破这种刚性联系，本文在计算$\Delta S_i$时添加了一定的高斯噪声，来人为的引入随机性干扰。
  视觉伺服阶段本文采用了Broyden更新方法，雅可比矩阵更新过程如下

控制律$A_t$的计算方法如下

创新点

• 提出一种基于互信息响应值的机器人自识别方法
• 采用视觉伺服控制的方式实现了机器人在形态学信息未知条件下的运动控制

算法评价

  本文的主要特点在于能够实现在高度自由的环境下对机器人进行视觉引导控制，无需准确的机器人形态学、动力学、运动学先验知识，无需精确的相机标定，甚至对于类似软体机器人这种对象都能进行控制，这赋予了该方法极大的应用范围，但与此同时我们也能感受到该方法的运动控制精确性是很难保证的，尤其是在单相机的条件下，很难在三维空间中完成精确的运动控制。

如果大家对于深度学习与计算机视觉领域感兴趣，希望获得更多的知识分享与最新的论文解读，欢迎关注我的个人公众号“深视”。