论文阅读笔记《Good match exploration using triangle constraint》

核心思想

  本文提出一种使用三角约束来获得更好匹配结果的图像匹配算法。作者认为现有的图像匹配方法，要么误匹配点太多，导致匹配率较低；要么总的匹配点数太少，使得许多应用都无法实现如三维重建。因此作者希望提出一种匹配点数量足够多，且误匹配点尽量少的匹配算法。由于现有的特征描述算法都只能对仿射变换保持不变性，而且仿射变换是现实场景中更加普遍的情况，因此作者针对存在仿射变换的两幅图像之间的匹配任务提出一种新的匹配方法。仿射变换包含六个自由度，利用三个不共线的点就可以得到，而任意给定三个不共线的点就能得到一个三角形。因此作者利用三角形约束来筛除误匹配的点。
  首先使用SIFT算法提取关键点和对应的特征向量，并且利用双向匹配法从中选择出候选的匹配点。所谓的双向匹配法就是图$I_A$中的点$A$其对应的匹配点是图$I_B$中的点$B$，且反过来图$I_B$中的点$B$对应的匹配点也是图$I_A$中的点$A$，这样才算是一对匹配点，如图中的黑色双向箭头表示的匹配点，否则都被筛除掉。

  然后对候选匹配点集进行Delaunay三角剖分，将其划分为三角形网格，如下图所示。

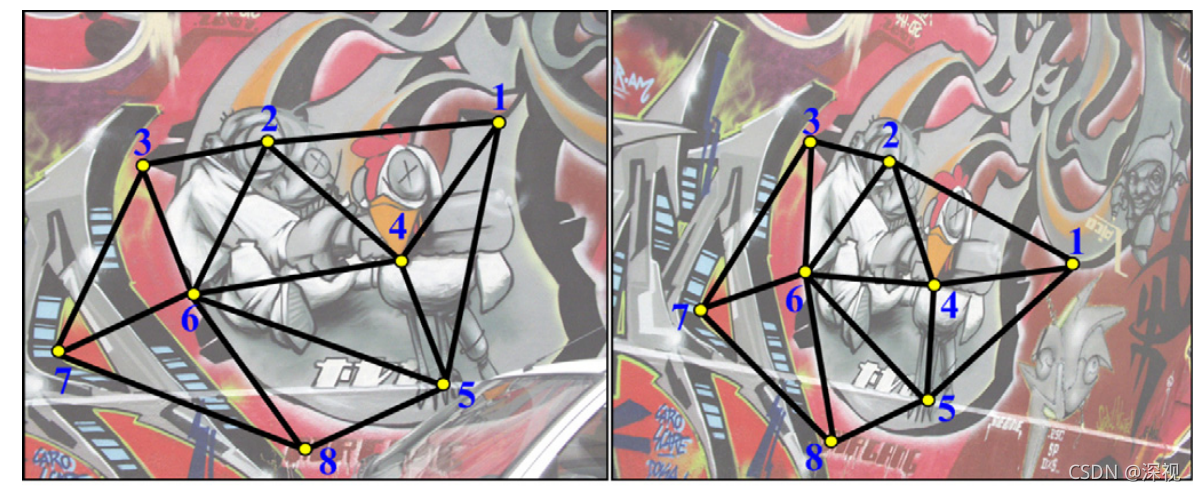
使用Delaunay三角剖分的好处是它不仅能够将稀疏点集划分成不重叠的三角网格，而且能够最大化每个三角形中的角度最小值。简单来说它能够避免哪种非常细长非常窄的三角形出现，这种三角形的三个点近似共线，不能很好的反映仿射变换关系。
  接下来就是最核心的三角约束了，从三角网格中任取一个三角形，如图中2、4、6点构成的三角形，并且将三个顶点重新命名为$a,b,c$，则其对应的匹配三角形为${△}_{a^{\prime }{b}^{\prime }{c}^{\prime }}$。将位于${△}_{abc}$内的特征点构成的点集称为${\mathcal{P}}_A$,将位于${△}_{a^{\prime }{b}^{\prime }{c}^{\prime }}$内的特征点构成的点集称为${\mathcal{P}}_B$，这里的特征点不是上面讲的候选匹配点，而是利用SIFT算法提取到所有特征点（双向匹配法筛除掉的部分），如下图中蓝色三角表示的部分。

  对于${\mathcal{P}}_A$中的任意一个特征点$P_i$，其齐次坐标满足以下关系

其中${\mathbf{P}}_i=[x_i,y_i,1{]}^T$,$\mathbf{a},\mathbf{b},\mathbf{c}$分别表示三角形三个顶点对应的齐次坐标，$\beta ,\gamma$表示放缩系数。进一步可得

其中$\alpha =1-\beta -\gamma$，而且可以证明如果${△}_{a^{\prime }{b}^{\prime }{c}^{\prime }}$和${△}_{abc}$之间满足仿射变换关系，那么${△}_{a^{\prime }{b}^{\prime }{c}^{\prime }}$中对应的匹配点$P_i^{\prime }$对应的参数${\mathbf{K}}^{\prime }$与$\mathbf{K}$相同。因此，根据$\mathbf{K}$和${△}_{a^{\prime }{b}^{\prime }{c}^{\prime }}$的三个顶点坐标，就可以求得$P_i$对应的估计匹配点$P_e$，如图中黑色圆点表示。

上述对应关系，只对翻转、旋转、放缩和仿射变换等过程成立，而对于透视变换不成立。但对于一个小的三角形局部，可以近似看作是仿射变换。
  为了提高算法的鲁棒性，在估计匹配点$P_e$附近半径为$R$范围都看作一个候选区域，如图中红色圆圈表示的范围，其中包含的特征点$C_j$都看作候选特征点，如图中绿色三角形表示。一个特征点对应的候选特征点可能有多个，因此用点集$\mathcal{C}=C_j$来表示。特征点$P_i$和候选特征点$C_j$之间的相似性得分可由下式表示

其中$dis{t}_{i,j}$表示齐次坐标${\mathbf{P}}_i$（这里我感觉应该是${\mathbf{P}}_e$）和${\mathbf{C}}_j$之间的欧氏距离，$D_i,D_{c_j}$分别表示点$P_i$和$C_j$对应的特征向量。上式中第一项描述了点$P_e$和$C_j$之间的空间距离，而点积$D_i^T{D}_{c_j}$则表示向量之间的相似性。
  如果对于候选特征点集$\mathcal{C}$中相似性得分最大的点超过阈值$\tau$，则该点被选为临时匹配点。每个特征点最多只有一个对应的临时匹配点，则对于每个三角形内的特征点集${\mathcal{P}}_A$都有一个对应的临时匹配点集$\mathcal{I}$，如果临时匹配点集中的匹配点数量满足以下条件

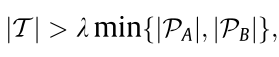
则这些临时匹配点被认为是最终的匹配点，否则这些临时匹配点就被抛弃。如果某个顶点相连的所有三角形都被筛除了，那么这个顶点也被认定为误匹配点，并将其筛除。筛除掉该点后，会导致三角形网格出现空洞，因此要对空洞区域重新进行三角剖分，来保持网格的完整性。

创新点

• 针对仿射变换提出一种新的三角几何约束，寻找到匹配点之间的某种联系
• 提出一种新的相似性度量方法，并据此选择临时匹配点

算法评价

  该方法主要是针对仿射变换提出一种新的几何约束，这就建立起了待匹配点和匹配点之间的一种关联，利用这一关系能够估计出匹配点大体所处的位置，然后从其邻域中选择出相似度最大的特征点作为临时匹配点，最后利用统计结果来判断当前划分的三角形之间是否是匹配的。通过这种方法一方面筛除掉部分误匹配点，即使这些点通过了双向匹配，还是有可能被该方法筛除掉，这样就提高了正确匹配率。另一方面还将许多被双向匹配法误筛除掉的匹配点补充进去，这就提高了匹配点的数量。

如果大家对于深度学习与计算机视觉领域感兴趣，希望获得更多的知识分享与最新的论文解读，欢迎关注我的个人公众号“深视”。