GNSS模糊度固定--混合整数最小二乘问题

limbo_250

已于 2024-06-12 09:33:30 修改

阅读量453

点赞数 5

文章标签：算法 gnss gps 最小二乘法

于 2024-05-25 01:15:24 首次发布

本文链接：https://blog.csdn.net/qq_36107898/article/details/136717713

版权

很多人都熟悉GNSS模糊度固定的过程，首先求模糊度实数估值，然后固定模糊度为整数，最后计算整数条件下其他参数（坐标等）的估值。

但是为何是这样的一个流程，其中的数学推导过程是怎么样的？我个人比较疑惑，因此仔细阅读了Tenissen大佬的文章《Least-Squares Estimation of The Integer GPS Ambiguities》,1993在此将我的理解分享给大家。

注：论文中提到 $A\left ( \cdot \right )$ 为非线性变换时，许多问题会变复杂，本人数学不好看不太懂，又因为GNSS模糊度求解中不涉及复杂的变换，因此下面的讨论，均在 $A\left ( \cdot \right )$ 为线性变换，且 $A$ 中均为实数的前提下展开。

一、GNSS观测方程模型

在本文中，我们将GNSS观测方程模型写作以下形式：

$y=Aa+Bb+e,a\in R^{n_{1}}, b\in Z^{n_{2}}$ （1）

其中各符号含义为：

$\boldsymbol{\mathbf{y}}$ - 观测值向量

$\boldsymbol{\mathbf{a}}$ - 测站坐标等参数向量，实数

$\mathbf{b}$ - 模糊度参数向量，整数

$\mathbf{A}$ 、 $\mathbf{B}$ - 坐标参数向量、模糊度参数向量的设计矩阵

$\mathbf{e}$ - 未模型化的误差向量

参数估计遵循最小二乘准则，即：

$min\left \| \mathbf{e} \right \|_{Q_{y}^{-1}}^{2}$ （2）

也即：

$min\left \| y-Aa-Bb\right \|_{Q_{y}^{-1}}^{2},a\in R^{n_{1}},b\in Z^{n_{2}}$ （3）

其中 $Q_{y}$ 是观测值 $\boldsymbol{\mathbf{y}}$ 的斜因数阵（或方差-协方差阵），它的逆即为观测值权阵。

二、最小二乘估计

1.等权的情况

下面先给出一般最小二乘解的公式：

对于观测方程：

$\mathbf{y}=\mathbf{Ax}+\mathbf{e}$ （4）

遵循最小二乘准则：

$min\left \| \mathbf{e} \right \|_{}^{2}$ （5）

其中， $\left \| e\right \|^{2}=e^{T}e$ ，也就是向量 $e$ 的模的平方。

那么，其最小二乘解应该为：

$\hat{x}=\left ( A^{T}A\right )^{-1}A^{T}y$ （6）

$\hat{e}=y-A\hat{x}$ （7）

该最小二乘问题的求解，从投影的角度很好理解：

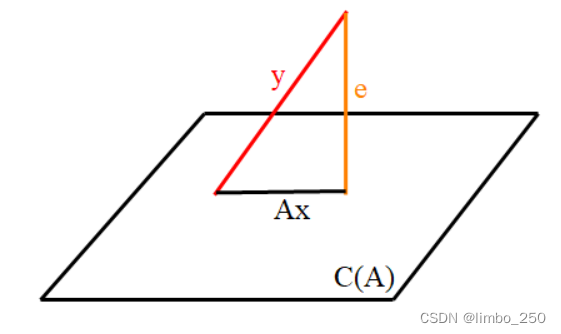
记A的列向量张成的空间为 $C\left ( A \right )$ ，那么 $Ax$ 在 $C\left ( A \right )$ 内，残差 $e$ 为 $y$ 与 $Ax$ 的差，最小二乘即是找到一个 $\hat{x}$ ，使残差向量 $e$ 的模最小。

很容易想到，残差向量 $e$ 与 $C\left ( A \right )$ 垂直时，其模最小，再根据向量与空间垂直的性质，有：

$A^{T}e=A^{T}(y-A\hat{x})=\vec{0}$ （8）

根据（8）式即可求得（6)、(7）式的最小二乘解。

2.加权的情况

由于观测值精度不同，我们会对不同的观测值赋予一个权重，这时观测方程仍为（4）式，但最小二乘准则变为了（2）式， $min\left \| \mathbf{e} \right \|_{Q_{y}^{-1}}^{2}$ ，其中：

$\left \| \mathbf{e} \right \|_{Q_{y}^{-1}}^{2}=\boldsymbol{e}^{T}Q_{y}^{-1}\boldsymbol{e}$ （9）

也即：

$\left \| \mathbf{y-Ax} \right \|_{Q_{y}^{-1}}^{2}=\boldsymbol{\left ( y-Ax \right )}^{T}Q_{y}^{-1}\boldsymbol{\left ( y-Ax \right )}$ （10）

其中 $Q_{y}$ 为观测值 $y$ 的方差，协方差矩阵， $Q_{y}^{-1}$ 即为权阵。

我们可以用目标函数对 $x$ 求导来求解，令

$\frac{d\left ( \boldsymbol{\left ( y-Ax \right )}^{T}Q_{y}^{-1}\boldsymbol{\left ( y-Ax \right )}\right )}{dx}=0$ （11）

可以解得：

$\hat{x}=\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}y$ （12）

此外，同样也可以从投影的角度来分析求解这个问题（个人理解，如有问题，请多批评指正）：

和上述的内容相同，我们知道，当残差向量 $e$ 与 $C\left ( A \right )$ 垂直时，其模最小，但是由于此时空间的度量发生了变化，向量内积的定义发生了变化（马氏距离？）：

$a\cdot b_{|Q^{-1}}=a^{T}Q^{-1}b$ （13）

因此，由 $e$ 与 $C\left ( A \right )$ 垂直得到：

$A^{T}e_{|Q_{y}^{-1}}=A^{T}Q_{y}^{-1}(y-A\hat{x})=\vec{0}$ （14）

由式（14）我们同样可以得到式（12）的解。

三、混合整数最小二乘问题

对于（3）式的最小二乘问题，我们不能直接遵循（5）式的最小二乘准则求解，因为其参数 $a$ 虽然不受限制，但 $b$ 被限制为整数。因此我们将这种问题称作混合整数最小二乘问题。

要解决混合整数最小二乘问题，我们先从整数最小二乘问题看起：

1.整数最小二乘

我们将（4）（5）式中的 $x$ 限制为整数，得到如下的两个式子，并将这样的问题称为整数最小二乘问题：

$\mathbf{y}=\mathbf{Ax}+\mathbf{e},x\in Z^{n}$ （15）

$min\left \| \mathbf{e} \right \|_{Q_{y}^{-1}}^{2},x\in Z^{n}$ （16）

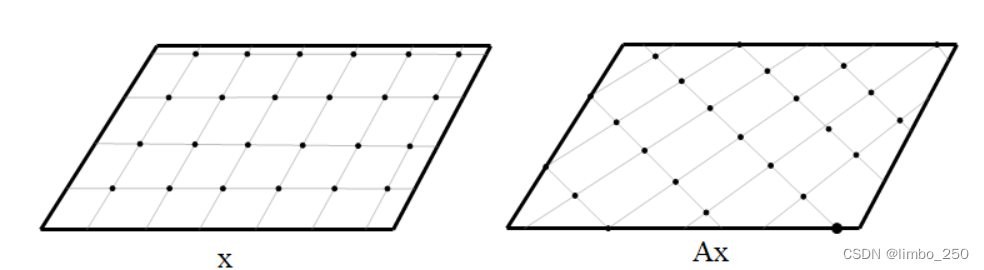
式（15）（16）与（4）（5）的区别就在于参数 $x$ 是否限制为整数，我们可以想象，当 $x$ 不受限制时， $Ax$ 是可以铺满 $C(A)$ 中的所有点的；但 $x$ 限制为整数后就不再如此。

$x \in Z^{n}$ 时，可以想象n维空间中有无数与坐标轴垂直的网格线， $x$ 就在这些格网点上。

经过 $A\left ( \cdot \right )$ 的线性转换，n维空间中的格网线被映射到 $C(A)$ 的子空间中，成维一系列非标准、倾斜的网格线， $x$ 则被映射到了新的格网点上，如下图：

结合下图可以看到，当 $x$ 受到限制后，要想残差向量 $e$ 的模最小，不能再取 $e$ 垂直于 $C(A)$ 时的解，因为根据上面的描述， $Ax$ 只能在格网点上移动，而垂点大概率是不在格网点上的。所以此时要求最小二乘解，是在要格网点中找出一个 $A\check{x}$ ，使 $\check{e} =y-A\check{x}$ 的模最小（注意参数上的帽子有正反之分）。

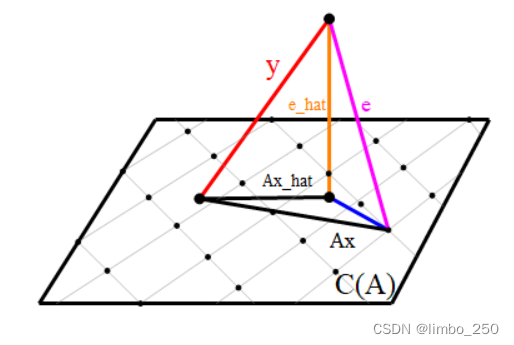
再进一步，我们先记垂直于 $C(A)$ 的解和残差向量分别为 $\hat{x}$ 和 $\hat{e}$ ，那么此时：

$\left \| e \right \|_{Q_{y}^{-1}}^{2} = \left \| y-Ax \right \|_{Q_{y}^{-1}}^{2}=\left \| \left ( A\hat{x} -Ax\right ) +\hat{e}\right \|_{Q_{y}^{-1}}^{2}$ （17）

由于 $A\left ( \hat{x} -x\right )\perp \hat{e}$ ，因此（17）式可进一步分解：

$\left \| e \right \|_{Q_{y}^{-1}}^{2}=\left \| \hat{e} \right \|_{Q_{y}^{-1}}^{2}+\left \| A\left ( \hat{x}-x \right ) \right \|_{Q_{y}^{-1}}^{2}$ （18）

其中， $\hat{e}$ 的值与 $x$ 无关，也就是说，式（18）等号右边第一项是常值，因此式（16）的最小二乘问题，转换成求解式（18）中等号右边第二项的最小值：

$min\left \| A\hat{x}-Ax \right \|_{Q_{y}^{-1}},x\in Z^{n}$ （19）

或： $min\left \|P_{A}y-Ax \right \|_{Q_{y}^{-1}},x\in Z^{n}$ （20）

其中， $P_{A}y$ 为 $C(A)$ 的投影矩阵，一般来说，可以由下式计算得到：

$P_{A}=A\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}$ （21）

于是，形如式（15）（16）这样的一个整数最小二乘问题，我们可以分两步来解决：

1）求解实数情况下的最小二乘问题，即式（18）等号右边的第一项

2）找到 $\check{x}$ ，使式（19）（20）取到最小值

式（20）写了一种不一样的形式，其实是因为这种形式在后续的推导中比较方便，式（20）与式（19）其实是一回事，矩阵 $P_{A}$ 将向量 $y$ 投影到 $C(A)$ 后就是 $A\hat{x}$ ，也就是说：

$P_{A}y=A\hat{x}$ （22）

2.混合整数最小二乘问题

当式（15）中的参数 $x$ 中一部分限制为整数，另一部分没有限制时，则变为式（1）（2）和（3）的形式，我们将这样的问题称为混合整数最小二乘问题（GNSS参数估计就是一个典型的混合整数最小二乘问题，其中模糊度参数为整数，其他参数为实数）：

$y=Aa+Bb+e,a\in R^{n_{1}}, b\in Z^{n_{2}}$ （1）

$min\left \| \mathbf{e} \right \|_{Q_{y}^{-1}}^{2}$ （2）

$min\left \| y-Aa-Bb\right \|_{Q_{y}^{-1}}^{2},a\in R^{n_{1}},b\in Z^{n_{2}}$ （3）

要解决这个问题，关键一步是对参数 $a$ 和 $b$ 进行重组：

$\begin{bmatrix} \tilde{a}\\ b \end{bmatrix}=\begin{bmatrix} I_{n_{1}} &\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}B \\ 0&I_{n_{2}} \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix}$ （23）

为什么要进行这么奇怪的重组呢，实际上我们是想利用投影矩阵 $P_{A}$ 和 ${P_{A}}^{\perp }$ 将 $Bb$ 分解到 $C(A)$ 和 $C(A)$ 的正交补空间里，即：

$Bb=P_{A}Bb+{P_{A}}^{\perp }Bb$ （24）

结合式（21），有

$Bb=A\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}Bb+{P_{A}}^{\perp }Bb$ （25）

于是：

$\begin{matrix} Aa+Bb& = & Aa+A\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}Bb+{P_{A}}^{\perp }Bb\\ & = & A\left \{ a+\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}Bb \right \}+{P_{A}}^{\perp }Bb \\ & = & A\tilde{a}+\tilde{B}b\end{matrix}$ （26）

其中：

$\tilde{a}=a+\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}Bb$ （27）

$\tilde{B}={P_{A}}^{\perp }B$ （28）

到这里我们就可以看出为什么要将原来的参数 $a$ 和 $b$ 参数进行式（23）展示的重组了。

参数重组之后，我们就可以把式（1）（3）的形式变换成下面的样子：

$y=A\tilde{a}+\tilde{B}b+e,\tilde{a}\in R^{n_{1}}, b\in Z^{n_{2}}$ （29）

$min\left \| y-A\tilde{a}-\tilde{B}b\right \|_{Q_{y}^{-1}}^{2},\tilde{a}\in R^{n_{1}}, b\in Z^{n_{2}}$ （30）

值得注意的是，此时 $\tilde{a}$ 为实数向量， $b$ 为整数向量。

要解决式（29）和（30）的问题，我们主要采取的方法是对式（30）的目标函数进行正交分解，为简化公式书写，在推导过程中我们忽略了下标 $Q_{y}^{-1}$ ，读者在自行推导的时候请记得加上。

1）第一次正交分解

首先，我们记 $C(A)$ 和 $C(\tilde{B})$ 这两个空间的并集为 $M$ 。

由式（28）知道， $C(\tilde{B})$ 是 $C(A)$ 正交补空间内的一个子空间，因此：

$C(\tilde{B})\perp C(A)$ （31）

那么，对于空间 $M$ 的投影矩阵 $P_{M}$ ，有：

$P_{M}=P_{A}+P_{\tilde{B}}$ （32）

接下来，我们进行第一次分解，将目标函数分解到空间 $M$ 和 $M^{\perp }$ ：

$\left \| y-A\tilde{a}-\tilde{B}b\right \|^{2}=\begin{matrix} \left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}\\ +\\ \left \| {P_{M}}^{\perp }\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2} \end{matrix}$ （33）

因为 $C(A)\subseteq M$ ， $C(\tilde{B})\subseteq M$ ，因此 $A\tilde{a}$ 和 $\tilde{B}b$ 投影到 $M^{\perp }$ 以后为 $\vec{0}$ ，所以式（33）进一步化为：

$\left \| y-A\tilde{a}-\tilde{B}b\right \|^{2}= \left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2} + \left \| {P_{M}}^{\perp } y\right \|^{2}$ （34）

可以看到，式（34）等号右边第二项与参数 $\tilde{a}$ 和 $b$ 的取值无关，因此目标函数的最小值仅取决于等号右边第一项，也就是说 $\left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}$ 取到最小值时， $\left \| y-A\tilde{a}-\tilde{B}b\right \|^{2}$ 也取到最小值。

2）第二次正交分解

接着我们对 $\left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}$ 进行正交分解，将式（32）带入，可得：

$\left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}=\begin{matrix} \left \| P_{A}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}\\ +\\ \left \| {P_{\tilde{B}}}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2} \end{matrix}$ （35）

显然 $A\tilde{a}$ 经过 $P_{A}$ 投影到 $C(A)$ 后就是 $A\tilde{a}$ 本身，由式（31）知道， $\tilde{B}b$ 经过 $P_{A}$ 投影到 $C(A)$ 后为 $\vec{0}$ 。

同样的 $A\tilde{a}$ 经 $P_{\tilde{B}}$ 投影后为 $\vec{0}$ ， $\tilde{B}b$ 经过 $P_{\tilde{B}}$ 投影后为 $\tilde{B}b$ 本身。

于是，式（35）变成：

$\left \| P_{M}\left ( y-A\tilde{a}-\tilde{B}b \right )\right \|^{2}=\left \| P_{A} y-A\tilde{a}\right \|^{2}+\left \| P_{\tilde{B}} y-\tilde{B}b\right \|^{2}$ （36）

经过两次正交分解，结合式（34）和式（36）我们可以看到，目标函数最终被分解为了如下的形式：

$\left \| y-A\tilde{a}-\tilde{B}b\right \|^{2}=\begin{matrix} \left \| {P_{M}}^{\perp } y\right \|^{2}\\ +\\ \left \| P_{A} y-A\tilde{a}\right \|^{2}\\ +\\\left \| P_{\tilde{B}} y-\tilde{B}b\right \|^{2} \end{matrix}$ （37）

3）求解目标函数最小值

到这里，请回忆最开始的目标：我们是希望求解参数 $\tilde{a}$ 和 $b$ ，让式（30）取最小值，根据等式（37），现在这个目标等价于等式右边三项的和取到最小值。

现在，我们来观察等式右边的三项：

首先，第一项 $\left \| {P_{M}}^{\perp } y\right \|^{2}$ 的结果常值的，与参数取值无关。

接着，第二项 $\left \| P_{A} y-A\tilde{a}\right \|^{2}$ ，注意在式（30）中我们提到过 $\tilde{a}\in R^{n_{1}}$ ，所以这一项的最小值是 0，并且仅当下式成立的时候取到 0：

$P_{A} y-A\tilde{a}=0$ （38）

我们将式（21）代入式（38），便可以得到参数 $\tilde{a}$ 的最小二乘解：

$\hat{\tilde{a}}=\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}y$ （39）

最后，我们来看第三项：因为 $b\in Z^{n_{2}}$ ，想要让这一项取最小值，其实就是我们在第 3.1 节中提到的整数最小二乘问题，也就是我们需要找到一个整数向量 $b$ ，使 $\left \| P_{\tilde{B}} y-\tilde{B}b\right \|^{2}$ 取得最小值。

那么整数向量 $b$ 为多少的时候能取得最小值呢，本篇文章中我们暂且按下不表，在这里姑且假设，通过某种方法我们已经找到了这个整数向量，我们将它记为 $\breve{b}$ 。那么依照式（37）的分解，我们现在便得到了目标函数的最小值，表示为下式：

$min\left \| y-A\tilde{a}-\tilde{B}b\right \|^{2}=\left \| {P_{M}}^{\perp } y\right \|^{2}+\left \| P_{\tilde{B}} y-\tilde{B}\breve{b}\right \|^{2}$ （40）

同时结合式（39）以及式（23）中参数 $\tilde{a}$ 与 $a b$ 的关系，我们可以得到参数 $ab$ 的解为：

$\begin{matrix} a & = & \tilde{a} - \left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}B\breve{b}\\ b & = &\check{b} \end{matrix}$ （41）

至此，混合整数最小二乘问题的求解就完毕了，回顾一下过程，我们通过两次正交分解，将式（30）的目标函数分解为了式（37）右边的三项，因为这三项的结果都是非负的，所以只要这三项分别取得最小值，目标函数就能取到最小值；最后我们依次分析了每一项的最小值为多少，并给出了各项取得最小值时参数的数值。

四、GNSS固定解求解

有了上面的分析，我们再来描述一下GNSS固定解求解的过程。

1.浮点解

一般来说，浮点解指的是我们舍弃模糊度参数的整数性质，将其当作实数，并通过最小二乘准则进行估计所求得的各参数的解。浮点解的求解过程同样可以从 3.2.2 节的正交分解开始，只不过在对式（37）等号右边第三项的最小值进行分析的时候，由于参数 $b$ 不再限制为整数向量，因此这一项的最小值可以取到 0，此时参数 $b$ 的解可根据下式求得：

$P_{\tilde{B}} y-\tilde{B}b=0$ （42）

我们记参数 $b$ 的浮点解为 $\hat{b}$ ，那么同样根据式（23）可以得到非模糊度参数的浮点解为：

$\hat{a}=\tilde{a} - \left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}B\breve{b}$ （43）

2.固定解

固定解则指的是我么们考虑模糊度参数的整数特性，将参数 $b$ 限制为整数时，求得的参数 $a$ 、 $b$ 的估值。求解固定解的关键在于3.2.3 节所述的找到一个整数向量 $\breve{b}$ （或者说一组整数）使式（37）右边的第三项取得最小值。

很遗憾，我们目前还没有一个像普通最小二乘一样，标准的方法，来找到这样一组整数，通常采取搜索的方式来解决这个问题，比如大家熟悉的LAMBDA方法（具体的方法原理会放到下一篇文章讲解）。

搜索的过程是先确定一个搜索的中心，一般来说，我们会选取模糊度的浮点解为中心（因为模糊度浮点值与固定值虽然不想等，但总归是比较接近的）。然后指定一个搜索范围，即确定以模糊度浮点值为中心的椭球的大小，在这个椭球中会有很多组整数备选解，我们最终会找到一个最优解。

在常见的代码中（如rtklib），我们通常会先根据式（42）、（43）来计算浮点解 $\hat{a}$ 、 $\hat{b}$ ，然后进行模糊度搜索，得到模糊度的固定解 $\breve{b}$ ，最后根据模糊度参数的变化量 $\hat{b}-\check{b}$ 得到非模糊度参数的固定解：

$\check{a}=\hat{a}-\left ( A^{T}Q_{y}^{-1}A \right )^{-1}A^{T}Q_{y}^{-1}B\left ( \hat{b}-\breve{b} \right )$ （44）

最后：本人才疏学浅，文章中如有问题，还望各位大佬多批评指正，感谢

limbo_250

关注

5
点赞
踩
10

收藏

觉得还不错? 一键收藏
0
评论
GNSS模糊度固定--混合整数最小二乘问题

很多人都熟悉GNSS模糊度固定的过程，首先求模糊度实数估值，然后固定模糊度为整数，最后计算整数条件下其他参数（坐标等）的估值。但是为何是这样的一个流程，其中的数学推导过程是怎么样的？我个人比较疑惑，因此仔细阅读了Tenissen大佬的文章在此将我的理解分享给大家。注：论文中提到为非线性变换时，许多问题会变复杂，本人数学不好看不太懂，又因为GNSS模糊度求解中不涉及复杂的变换，因此下面的讨论，均在为线性变换，且中均为实数的前提下展开。
复制链接

扫一扫