NumPy矩阵的创建、遍历与常见运算

最新推荐文章于 2023-05-14 11:19:24 发布

飞机火车巴雷特

最新推荐文章于 2023-05-14 11:19:24 发布

阅读量7.1k

点赞数 8

分类专栏： Python相关文章标签： numpy python 矩阵

本文链接：https://blog.csdn.net/qq_36158230/article/details/117717014

版权

Python相关专栏收录该内容

61 篇文章 1 订阅

订阅专栏

NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。其前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发，2005 年，Travis Oliphant在Numeric中结合了另一个同性质的程序库Numarray的特色，并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。NumPy 是一个运行速度非常快的数学库，主要用于数组计算，包含：

1. 一个强大的N维数组对象 ndarray；
2. 广播功能函数；
3. 整合 C/C++/Fortran 代码的工具；
4. 线性代数、傅里叶变换、随机数生成等功能...

在使用NumPy库之前，应先导入其包，一下是常见的导入方式（推荐）：

import numpy as np; # 此方式使用numpy的函数时需要以np.开头

或者用以下方式（可直接调用mat()或者其他库函数，不需以np.开头）：

from numpy import *;    # 导入numpy的库函数

一、矩阵创建

代码：

import numpy as np

print(np.mat(np.zeros((3, 3))))             # 输出一个3×3的零矩阵（数据默认类型为浮点数）
print(np.mat(np.ones((2, 4))))              # 输出一个2×4的全一矩阵
print(np.mat(np.ones((2, 4)), dtype=int))   # 输出一个2×4的全一矩阵（int类型）
print(np.mat(np.random.rand(2, 2)))         # 输出一个2×2的随机数矩阵（由2*2NumPy数组转化得到）
print(np.mat(np.random.randint(0, 10, size=(3, 3))))   # 输出一个3×3的随机数矩阵（其值位于[0, 10)）
print(np.mat(np.eye(2, 2, dtype=int)))      # 输出一个2×2的对角单位矩阵
print(np.mat(np.diag([1, 2, 3])))           # 输出一个对角线元素为1、2、3的对角矩阵

输出：

[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

[[1. 1. 1. 1.]
 [1. 1. 1. 1.]]

[[1 1 1 1]
 [1 1 1 1]]

[[0.38331668 0.29764027]
 [0.6652657  0.82721648]]

[[5 5 3]
 [4 2 0]
 [3 3 1]]

[[1 0]
 [0 1]]

[[1 0 0]
 [0 2 0]
 [0 0 3]]

二、矩阵遍历

矩阵的遍历这里是指通过两层循环迭代，得到第i行j列元素，对于这个第i行第j列元素，我们既可以读取它，也可以改变它。代码如下：

import numpy as np

# 矩阵遍历
def mat_traverse(mat):
    rows, cols = mat.shape              # 获取矩阵的行数和列数
    for i in range(rows):               # 按照行来遍历
        for j in range(cols):           # 对第i行进行遍历
            print(mat[i, j], end=' ')   # 输出第i行第j列元素（读）
            mat[i, j] = 9               # 改变第i行第j列元素（写）

a = np.mat(np.random.randint(0, 10, size=(3, 4)))   # 生成3×4的矩阵
print(a)            # 打印
mat_traverse(a)     # 遍历
print()
print(a)            # 再打印，预期输出：全是9

输出：

[[8 4 5 5]
 [5 8 3 2]
 [4 9 9 0]]

8 4 5 5 5 8 3 2 4 9 9 0 

[[9 9 9 9]
 [9 9 9 9]
 [9 9 9 9]]

三、矩阵常见运算

1. 矩阵加减法。矩阵加法是指m×n的矩阵和m×n的矩阵相加减得到m×n的矩阵。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
b = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
c = a + b   # 得到3×2矩阵
d = a - b   # 得到3×2矩阵
print(a)
print(b)
print(c)
print(d)

输出：

[[7 9]
 [7 8]
 [5 1]]

[[0 4]
 [7 5]
 [1 5]]

[[ 7 13]
 [14 13]
 [ 6  6]]

[[ 7  5]
 [ 0  3]
 [ 4 -4]]

2. 矩阵乘积。矩阵乘积是指m×n的矩阵和n×s的矩阵相乘得到m×s的矩阵。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 4)))   # 3×4矩阵
b = np.mat(np.random.randint(0, 10, size=(4, 2)))   # 4×2矩阵
c = a * b           # 得到3×2矩阵 在mat中*运算与np.dot、np.matmul运算是等价的
d = np.dot(a, b)    # 得到3×2矩阵 在mat中*运算与np.dot、np.matmul运算是等价的
e = np.matmul(a, b) # 得到3×2矩阵 在mat中*运算与np.dot、np.matmul运算是等价的
print(a)
print(b)
print(c)
print(d)
print(e)

输出：

[[5 0 9 7]
 [5 9 8 4]
 [9 1 9 4]]

[[4 2]
 [3 6]
 [0 5]
 [7 5]]

[[ 69  90]
 [ 75 124]
 [ 67  89]]

[[ 69  90]
 [ 75 124]
 [ 67  89]]

[[ 69  90]
 [ 75 124]
 [ 67  89]]

3. 矩阵Hadamard积(multiply)。矩阵Hadamard积是指m×n的矩阵和m×n的矩阵进行点乘得到m×n的矩阵，代码：

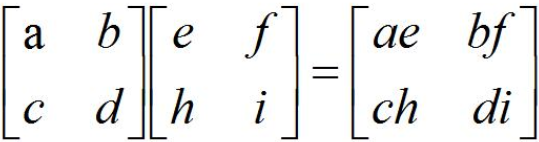
import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
b = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
c = np.multiply(a, b)   # 得到3×2矩阵
print(a)
print(b)
print(c)

输出：

[[5 2]
 [4 2]
 [8 3]]

[[8 6]
 [9 0]
 [9 9]]

[[40 12]
 [36  0]
 [72 27]]

4. 矩阵内积。矩阵内积是指m×n的矩阵和m×n的矩阵进行内积得到一个标量。它不能通过调用NumPy中的inner运算得到。两个矩阵（均为m×n）的内积是一个矩阵的第i个列向量转置与另一个矩阵的第i个列向量进行向量内积然后通过求和得到的，其结果是一个标量数值。假设两个矩阵分别为 $\mathbf{A}$ 和 $\mathbf{B}$ ，其内积 $\left \langle \mathbf{A}, \mathbf{B} \right \rangle$ 具体计算公式为：

$\left \langle \mathbf{A}, \mathbf{B} \right \rangle = \sum_{i=1}^{n}\mathbf{a}_{i}^{T}\mathbf{b}_i \quad where \quad \mathbf{a}_i = \begin{bmatrix} a_{1i}\\ \vdots \\ a_{mi} \end{bmatrix}\quad and \quad \mathbf{b}_i = \begin{bmatrix} b_{1i}\\ \vdots \\ b_{mi} \end{bmatrix}\newline$

代码：

import numpy as np

# 计算矩阵内积
def mat_inner_product(mat_a, mat_b):
    # 获取两个矩阵的行列
    am, an = mat_a.shape
    bm, bn = mat_b.shape
    # 判断矩阵的行列是否相同
    # 若不相同，则抛出异常
    if am != bm or an != bn:
        raise Exception("operands could not be broadcast together with shapes (%s,"
                        "%s) (%s,%s)" % (str(am), str(an), str(bm), str(bn)))
    # 若相同，则根据公式计算矩阵内积
    else:
        inner_product = 0
        for i in range(an):
            # 计算矩阵a第i个列向量转置乘以矩阵b第i个列向量
            inner_product = inner_product + mat_a[:, i].T * mat_b[:, i]
        # 返回内积
        return inner_product

# 测试
a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
b = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
c = np.mat(np.random.randint(0, 10, size=(4, 2)))   # 4×2矩阵
print(a)
print(b)
print(c)
print(mat_inner_product(a, b))    # 相同shape计算（预期输出：正确计算）
print(mat_inner_product(a, c))    # 不同shape计算（预期输出：抛出异常）

输出：

[[6 3]
 [7 2]
 [4 2]]

[[5 2]
 [7 8]
 [2 2]]

[[0 7]
 [1 5]
 [3 5]
 [9 0]]

[[113]]

Traceback (most recent call last):
  File "***.py", line 24, in <module>
    print(mat_inner_product(a, c))
  File "***.py", line 9, in mat_inner_product
    "%s) (%s,%s)" % (str(am), str(an), str(bm), str(bn)))
Exception: operands could not be broadcast together with shapes (3,2) (4,2)

Process finished with exit code 1

注意，NumPy中的inner运算( $\mathbb{R}^{m\times n} \quad inner \quad \mathbb{R}^{r\times n} \rightarrow \mathbb{R}^{m\times r}$ )不是计算矩阵内积的方法。inner运算的例子如下：

$\begin{bmatrix} 5&8\\ 2&0\\ 3&0 \end{bmatrix} inner \begin{bmatrix} 1&2\\ 5&8\\ 1&8 \end{bmatrix}=\begin{bmatrix} 21&89&69\\ 2&10&2\\ 3&15&3 \end{bmatrix}$

$\begin{bmatrix} 5&8\\ 2&0\\ 3&0 \end{bmatrix} inner \begin{bmatrix} 7&0\\ 2&8\\ 3&5 \\8&9 \end{bmatrix}=\begin{bmatrix} 35&74&55&112\\ 14&4&6&16\\ 21&6&9&24 \end{bmatrix}$

5. 矩阵转置。矩阵转置是指m×n的矩阵转置成一个n×m的矩阵。其实上面在求矩阵内积的时候已经使用过。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
b = np.mat(np.random.randint(0, 10, size=(2, 2)))   # 2×2矩阵
print(a)    # 输出矩阵a
print(a.T)  # 输出矩阵a的转置
print(b)    # 输出矩阵b
print(b.T)  # 输出矩阵b的转置

输出：

[[2 7]
 [8 5]
 [0 8]]

[[2 8 0]
 [7 5 8]]

[[5 0]
 [4 6]]

[[5 4]
 [0 6]]

6. 矩阵求逆。逆矩阵是针对正方矩阵（即n×n矩阵）而言的，并且不是所有的矩阵都可逆。矩阵可逆的充要条件是矩阵所对应的行列式的值不等于0，即，对于n阶矩阵 $\mathbf{A}$ ，若 $det(\mathbf{A})\neq 0$ 或 $|\mathbf{A}|\neq 0$ ，则说明矩阵 $\mathbf{A}$ 可逆。当然，这只是判断矩阵可逆的其中一个条件（另外的充要条件还可参考此文章）。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(2, 2)))   # 2×2矩阵
b = np.mat(np.random.randint(0, 1, size=(2, 2)))    # 2×2零矩阵
print(a)
print(b)
det_a = np.linalg.det(a)    # 计算矩阵a对应的行列式的值
det_b = np.linalg.det(b)    # 计算矩阵b对应的行列式的值
if det_a != 0:
    print(a.I)              # 存在逆矩阵的情况下对矩阵求逆
if det_b != 0:
    print(b.I)

输出：

[[2 2]
 [6 7]]

[[0 0]
 [0 0]]

[[ 3.5 -1. ]
 [-3.   1. ]]

7. 矩阵求秩。矩阵 $\mathbf{A}_{m \times n}$ 的秩定义为该矩阵中线性无关的行或列的数目。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
b = np.mat(np.random.randint(0, 10, size=(3, 4)))   # 3×4矩阵
c = np.mat(np.random.randint(0, 1, size=(2, 2)))    # 2×2零矩阵
d = np.mat([[1, 0], [0, 0]])                        # 2×2矩阵
print(a)
print(b)
print(c)
print(d)
print(np.linalg.matrix_rank(a))     # 矩阵求秩
print(np.linalg.matrix_rank(b))     # 矩阵求秩
print(np.linalg.matrix_rank(c))     # 矩阵求秩
print(np.linalg.matrix_rank(d))     # 矩阵求秩

输出：

[[4 4]
 [4 3]
 [2 1]]

[[1 0 3 2]
 [1 8 4 4]
 [1 8 3 9]]

[[0 0]
 [0 0]]

[[1 0]
 [0 0]]

2
3
0
1

8. 矩阵求特征值和特征向量。对于m×n的矩阵而言，它最多有min{m, n}个不同的特征值。但在NumPy中，求矩阵的特征值和特征向量要求该矩阵必须是一个正方矩阵（查了一下资料，好像没找到m×n矩阵求特征值和特征向量的方法，如果您知道请留言告诉博主）。根据源码中的备注可知，NumPy求矩阵特征值和特征向量后会返回一个NumPy数组和一个NumPy矩阵，其中，数组中的第i个数是所求得的第i个特征值，而矩阵（已经过归一化）中的第i列是所求得的第i个特征向量，第i个特征值与第i个特征向量是相对应的。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 3)))   # 3×3矩阵
b = np.mat(np.random.randint(0, 10, size=(2, 2)))   # 2×2矩阵
c = np.mat(np.random.randint(0, 1, size=(2, 2)))    # 2×2零矩阵
d = np.mat([[1, 0], [0, 0]])                        # 自定义2×2矩阵
print(a)
print(b)
print(c)
print(d)
print(np.linalg.eig(a))     # 矩阵求特征值与特征向量
print(np.linalg.eig(b))     # 矩阵求特征值与特征向量
print(np.linalg.eig(c))     # 矩阵求特征值与特征向量
print(np.linalg.eig(d))     # 矩阵求特征值与特征向量

输出：

[[9 0 3]
 [7 3 9]
 [2 7 2]]

[[5 0]
 [4 0]]

[[0 0]
 [0 0]]

[[1 0]
 [0 0]]

(array([13.14761616,  5.8473039 , -4.99492006]), 
matrix([[-0.38976728, -0.59238197, -0.15446849],
        [-0.74679472,  0.51140562, -0.67593458],
        [-0.53886836,  0.62253345,  0.72059137]]))

(array([0., 5.]), 
matrix([[0.        , 0.78086881],
        [1.        , 0.62469505]]))

(array([0., 0.]), 
matrix([[1., 0.],
        [0., 1.]]))

(array([1., 0.]), 
matrix([[1., 0.],
        [0., 1.]]))

9. 矩阵求迹。迹也是针对正方矩阵而言的概念。迹的计算思想是求矩阵的对角元素之和。对于正方矩阵 $\mathbf{A}_{n \times n}$ ，其迹记作 $tr(\mathbf{A})$ 。计算公式和在NumPy中的调用代码如下：

$tr(\mathbf{A}) = a_{11} + a_{22} + ... + a_{nn} = \sum_{i=1}^{n}a_{ii}$

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 3)))   # 3×3矩阵
b = np.mat(np.random.randint(0, 10, size=(2, 2)))   # 2×2矩阵
c = np.mat(np.random.randint(0, 1, size=(2, 2)))    # 2×2零矩阵
d = np.mat([[1, 0], [0, 0]])                        # 自定义2×2矩阵
print(a)
print(b)
print(c)
print(d)
print(a.trace())    # 矩阵求迹
print(b.trace())    # 矩阵求迹
print(c.trace())    # 矩阵求迹
print(d.trace())    # 矩阵求迹

输出：

[[9 1 0]
 [5 7 9]
 [8 2 2]]

[[8 4]
 [9 9]]

[[0 0]
 [0 0]]

[[1 0]
 [0 0]]

[[18]]
[[17]]
[[0]]
[[1]]

9. 矩阵求行和、列和、元素之和、列元素最大值、行元素最大值、列元素最小值、行元素最小值。代码：

import numpy as np

a = np.mat(np.random.randint(0, 10, size=(3, 2)))   # 3×2矩阵
print(a)
print(a.sum(axis=0))    # 矩阵求列和 得到1×2矩阵（自上而下求和）
print(a.sum(axis=1))    # 矩阵求行和 得到3×1矩阵（自左向右求和）
print(a.sum())          # 矩阵求所有元素之和 得到的是标量

print(a.max(axis=0))    # 矩阵求列元素最大值 得到1×2矩阵（自上而下求最大值）
print(a.max(axis=1))    # 矩阵求行元素最大值 得到3×1矩阵（自左向右求最大值）
print(a.max())          # 矩阵求所有元素最大值 得到的是标量

print(a.min(axis=0))    # 矩阵求列元素最小值 得到1×2矩阵（自上而下求最小值）
print(a.min(axis=1))    # 矩阵求行元素最小值 得到3×1矩阵（自左向右求最小值）
print(a.min())          # 矩阵求所有元素最小值 得到的是标量

输出：

# 矩阵
[[7 0]
 [6 7]
 [5 9]]
# 列和
[[18 16]]
# 行和
[[ 7]
 [13]
 [14]]
# 所有元素之和
34

# 列元素最大值
[[7 9]]
# 行元素最大值
[[7]
 [7]
 [9]]
# 所有元素最大值
9

# 列元素最小值
[[5 0]]
# 行元素最小值
[[0]
 [6]
 [5]]
# 所有元素最小值
0

10. 矩阵的分割。将从原矩阵得到一个子矩阵。代码：

import numpy as np

# 分割说明
# 对于m×n矩阵以下a和b都是整数，范围是[0, m]或[0, n]
# 若a=0，它表示矩阵第0+1列或0+1行
# ' : ' 全选
# 'a: ' 从a起到最后，包括a
# ' :a' 从0到a，包括0，不包括a
# 'a:b' 从a到b，包括a，不包括b
m = np.mat(np.random.randint(0, 10, size=(3, 4)))   # 3×4矩阵
print(m)
print(m[:, 0])          # 由第1列元素组成的矩阵
print(m[2, :])          # 由第3行元素组成的矩阵
print(m[0: 3, 1])       # 由第1行到3行，第2列组成的矩阵
print(m[0, 1: 3])       # 由第1行，第2列到第3列组成的矩阵
print(m[0: 3, 1: 3])    # 由第1行到3行，第2列到第3列组成的矩阵

输出：

[[0 1 9 5]
 [9 5 5 5]
 [8 4 7 3]]

[[0]
 [9]
 [8]]

[[8 4 7 3]]

[[1]
 [5]
 [4]]

[[1 9]]

[[1 9]
 [5 5]
 [4 7]]

11. 矩阵合并。矩阵合并是指行数相同的矩阵左右合并或者列数相同的矩阵上下合并。值得注意的是，如果行数不相同进行左右合并或者列数不相同进行上下合并程序会出现异常报错。例如：

$\begin{bmatrix} 1&1 \\ 1&1 \\ 1&1 \end{bmatrix}\begin{bmatrix} 0&0 &0 \\ 0& 0&0 \\ 0& 0&0 \end{bmatrix}\rightarrow \begin{bmatrix} 1& 1& 0& 0&0 \\ 1& 1& 0& 0&0 \\ 1& 1& 0& 0&0 \end{bmatrix}$

$\begin{bmatrix} 0& 0& 0&0 \\ 0& 0& 0&0 \end{bmatrix}\begin{bmatrix} 1& 1& 1&1 \end{bmatrix}\rightarrow \begin{bmatrix} 0& 0& 0&0 \\ 0& 0& 0&0 \\ 1& 1& 1&1 \end{bmatrix}$

代码：

import numpy as np

a = np.mat(np.ones((3, 4)), dtype=int)    # 3×4矩阵
b = np.mat(np.zeros((3, 3)), dtype=int)   # 3×3矩阵
c = np.mat(np.zeros((2, 4)), dtype=int)   # 2×4矩阵
d = np.mat(np.ones((1, 4)), dtype=int)    # 1×4矩阵
print(a)
print(b)
print(np.hstack((a, b)))  # 左右合并（行相同）
print(c)
print(d)
print(np.vstack((c, d)))  # 上下合并（列相同）

输出：

[[1 1 1 1]
 [1 1 1 1]
 [1 1 1 1]]

[[0 0 0]
 [0 0 0]
 [0 0 0]]

[[1 1 1 1 0 0 0]
 [1 1 1 1 0 0 0]
 [1 1 1 1 0 0 0]]

[[0 0 0 0]
 [0 0 0 0]]

[[1 1 1 1]]

[[0 0 0 0]
 [0 0 0 0]
 [1 1 1 1]]

12. 1×1矩阵的值与标量数值的相互转换。例如[[10]]和10的互换。

import numpy as np

val1 = 10
# 标量数值->1×1矩阵
a = np.mat(val1, dtype=int)
print(a)    # 输出1×1矩阵

# 1×1矩阵->标量数值
val2 = a[0, 0]
print(val2) # 输出标量数值

输出：

[[10]]
10

四、结束语

1. 以上的输出中，每个矩阵之间我手动加了一行，以方便更直观地分析和观察计算过程；

2. 以上内容均是经过矩阵分析的理论学习和实践所作的总结，个人能力有限，如有错误请大胆批评指正，谢谢！

3. 如果有想要添加或者觉得缺少的内容请留言，博主将不定期更新此博客。

参考资料

1. 菜鸟教程之NumPy教程。

2. CSDN博客：python的常见矩阵运算。

3. CSDN博客：python中numpy模块函数array()和mat()的区别。

4. 看过但忘了记录的文献...

飞机火车巴雷特

关注

8
点赞
踩
48

收藏

觉得还不错? 一键收藏
打赏
7
评论
NumPy矩阵的创建、遍历与常见运算

numpy常用矩阵运算：创建、遍历、矩阵加减、矩阵乘积、矩阵Hadamard积(multiply)、矩阵内积、矩阵转置、矩阵求逆、矩阵求秩、矩阵求特征值和特征向量、矩阵求迹、矩阵求行和、列和、元素之和、列元素最大值、行元素最大值、列元素最小值、行元素最小值、矩阵分割、矩阵合并
复制链接

扫一扫