递推最小二乘法——Matlab实现算法

递推最小二乘法

主要用于求解超定方程的未知解

实现代码见博客最下方

---

算法实现

• 利用递推最小二乘法，求解Ax=b的解
• A为m*x维的矩阵，元素服从独立同分布的正态分布
• b为m维的已知向量，元素也是服从独立同分布的正态分布

设计思路

• 首先设置好迭代所需要的初始参数
• 将A中的10000个方程提取出来，依次做10000次迭代
• 最后将每一次迭代的x的结果输出

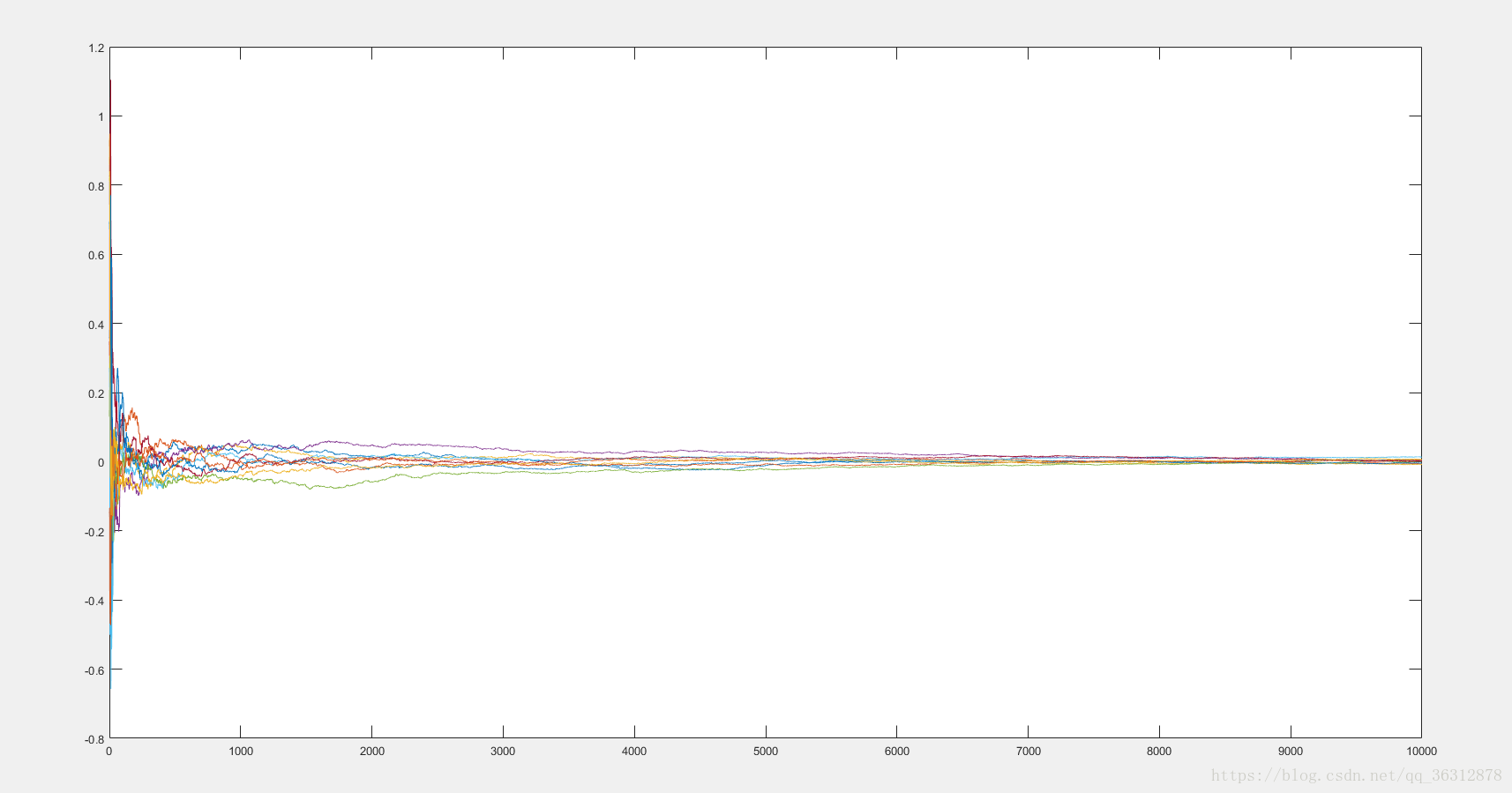
数值实验

• 递推最小二乘法未知解
  

结果分析

• 由上图可以得知，由于一开始的未知解是随机生成的，误差比较大，经过了10000次的迭代之后，开始震荡收敛于某个值。因为随机生成的矩阵的元素是正态分布的，因此10个未知解都大致收敛于0附近的值上。

代码实现

clear;
format long;
A = randn([10000 10]);
b = randn([10000 1]);
x = rand(10,1);
I = eye(10, 10);
P = (10^6) * I;

for k = 1:10000
    Ak = A(k,:);
    Q1 = P*(Ak');
    Q2 = 1 + Ak * P * (Ak');
    Q = Q1/Q2;
    x = x + Q * (b(k) - Ak*x);
    P = (I - Q*Ak)*P;
    result2(:,k) = x;
    result1(k) = k;
end
result1 = result1';
%result = [result1; result2];
plot(result1, result2);