【高级数据库】第二章第04讲多维索引

最新推荐文章于 2023-12-08 16:56:00 发布

华师数据学院·王嘉宁

最新推荐文章于 2023-12-08 16:56:00 发布

阅读量2.3k

点赞数 4

分类专栏：数据库文章标签：高级数据库多维索引多维散列

本文链接：https://blog.csdn.net/qq_36426650/article/details/103324224

版权

数据库专栏收录该内容

8 篇文章

订阅专栏

【高级数据库】第二章数据库索引

前面讲解了几种索引的数据结构，但这些索引键都是一维的。对于多维查询（例如查询同时满足两个键的记录），可以通过多次执行一维索引实现，但对于更加复杂的数据这种方法显然不可取，因此需要扩展多维索引。多维索引结构主要分为两类：
（1）类散列表：包括网格文件、分段散列；
（2）类树：包括多键索引、kd-树、四叉树、R-树。
最后我们会拓展一种特别的索引结构——位图索引。

第04讲多维索引

1、多维数据的散列结构

多维数据的散列结构包括网格文件和分段散列，下面介绍网格文件：

1.1 网格文件

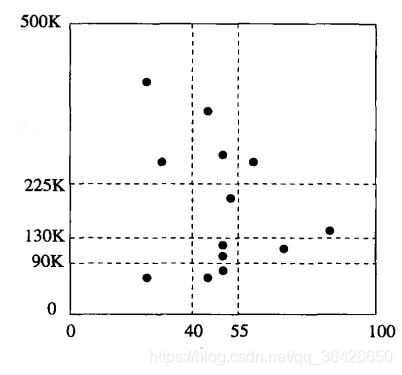
网格文件是一种改进单维索引的数据结构，根据查询的范围可以为每一个维度划分三个区域，形成网格状。假设有一个查询涉及到两个查找键 $X, Y$ ，查询的范围为 $X\in[40,55),Y\in[90,225)$ ，因此可以分别在两个维度上划分三个区域，形成九个网格，每个网格内存储的是符合 $X, Y$ 所在范围内的记录，其指针指向对应的桶，假设桶中最大存储2个记录。如图所示：
在这里插入图片描述
左图为网格文件，一共划分9个区域，其中正中间区域即为查询的部分，右图表示每个网格对应的桶，所要查询的桶即为红色区域及对应的记录。
（1）网格文件的查询：当要查询指定范围的记录时，根据查询键的数量建立对应维度的网格文件，其次为每个区域设计或选择合适的散列函数，将次区域映射到对应的桶地址（或桶中第一个记录的地址），然后取出桶中全部数据即可。
（2）网格文件的插入：遵循查询方法的同时，需要向桶中插入新记录及键，如果桶未满则直接插入即可，否则需要解决溢出问题。
一般解决溢出问题，可以设置一个溢出块，即在桶的基础上扩充新的空间；另一种则是重新划分网格线。例如插入一个数据 $(X = 52, Y = 200)$ ，可知其所在中间的网格，但其空间已满，此时可以添加一个水平网格线 $Y = 130$ 将该桶划分为两个。划分桶需要注意尽可能的减少空桶的数量（完全不产生空桶是不可能的，因此需要尽可能减少），如图：
在这里插入图片描述

1.2 分段散列

分段散列通常是设计一个散列函数可以对多维数据同时进行索引。例如二维数据 $(X, Y)$ ，通常设计一个散列函数 $h (X, Y)$ 将两个键分别转换为二进制表示。设散列值维度为 $k$ ，对应的键分别为 $h (X), h (Y)$ 维度为 $k_X,k_Y$ ，且有 $k_X+k_Y=k$ 。例如对于如下8个二维键：
在这里插入图片描述
其中第一个键 $X$ 我们划分0表示奇数和1表示偶数，第二个键 $Y$ 划分模4的余数，0表示余数为0，1表示余数为1，2表示余数为2，3表示余数为3，因此可以组合为三个二进制数。例如对于 $(25, 60)$ 则有 $h (25, 60) = 100$ 。所有数据的索引图如图所示：
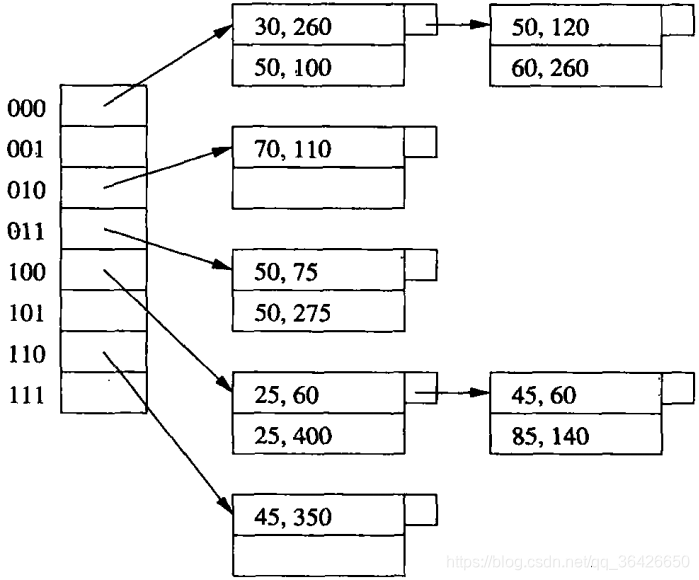
在这里插入图片描述
可以发现，分段散列表可以使用链地址法存储，左侧表示数组，数组下标恰巧为二进制键值的十进制表示，数组存储指向对应桶的指针，每个结点可以是固定尺寸的存储快，也可以用链表依次相连。

2、多维数据的树结构

除了散列结构外，树结构也可以用于多维数据的索引，包括四种树形结构：多键索引、kd-树、四叉树和R-树。前三种用于点集，R-树用于点集或区间集。

2.1 多键索引

多键索引是指在树上对每个结点设置索引的数据结构。假设有二维键 $(X, Y)$ ，则根结点是第一个键 $X$ 的索引，其次第二层上的结点则是 $Y$ 对应的索引。如图所示：
在这里插入图片描述
例如查询 $(X = 50, Y = 120)$ 的记录，首先在根结点查询键为50的指针，其次根据指针索引第二层第四个树结点，在依次进行匹配。如果维数超过2维，则在基础上继续添加一层用于对第三个键添加索引。此存在一个问题是树根结点默认的为键 $X$ 设置索引，而如若首先查询 $Y$ 的键，则只能在第二层一个个查询了。

2.2 kd-树

kd-树是一种将二叉搜索树推广到多维数据的数据结构，其每个内结点只代表一个属性（键），左右孩子分别是对应属性（键）根据某一个值划分的两部分。如图：
在这里插入图片描述
这是一个二叉排序树，也非常像机器学习中的决策树，其最终的记录全部存在叶子结点上。如若插入一个新记录，首先进行查找，如果找到其所在额叶子结点对应的桶中还有空间，则插入，否则执行结点分裂，这与【B-树】一节的插入操作一样。

2.3 四叉树

四叉树相比于kd-树来说划分的角度不同。kd-树是每个结点仅划分一个属性，而四叉树是划分多个属性的组合。例如二维键 $(X, Y)$ ，四叉树的每个内部结点则是根据当前的值 $(X, Y)$ 划分四个区域，按照坐标象限的顺序定义，分别为
$\text{I}:\{(x,y)|x>X,y>Y\}$
$\text{II}:\{(x,y)|x\leq X,y>Y\}$
$\text{III}:\{(x,y)|x\leq X,y\leq Y\}$
$\text{IV}:\{(x,y)|x>X,y\leq Y\}$
最终叶子结点存储对应的桶，假设桶最大存储空间为2。
当然如果当前结点划分后区域内已经满足小于等于2个记录，则终止划分，否则继续划分。如图所示：
在这里插入图片描述
这是一个四叉树的划分图，第一次划分以 $(X = 50, Y = 200)$ 点对应的四个区域，其中 $I$ 和 $I I I$ 象限内恰巧有两个记录，则停止划分，另两个结点对应超过2个记录，因此继续划分。一个维度上的划分点取当前区间范围内的中位数。

2.4 R-树（区域树）

R-树是可以查询指定一个区域，其每个结点表示一个区域范围，且这个结点的子结点区域是这个结点区域的子集，所有子结点的区域可重叠。例如：
在这里插入图片描述

外面的实线框表示R-树中的一个内部结点，该结点存储两个坐标（左上角和右下角的坐标），其子结点包含四个（相当于四个孩子结点），每个子结点与这个结点一样存储两个坐标。因此四个孩子结点表示的区域为虚线框。叶子结点也表示一个区域，这个区域内对应的内容即为记录。
当查询一个指定区域时，即可通过坐标大小比较方法缩小区域，直到找到指定的叶子结点。若在指定区域内插入一个记录，则首先进行查询，若叶子结点对应的桶有空余空间，则直接插入，否则需要分裂叶子结点，分裂方法与前述一样。

另一种索引用于描述多维数据的方式是位图索引。位图索引目标是为指定字段相应不同取值进行向量化表示。

3、位图索引

假设一文件包含记录 $n$ 个，字段（属性） $m$ 个，所有记录中第 $k$ 个字段可有 $m_k$ 个取值。因此对于第 $k$ 个字段的第 $t$ 个取值可用0-1向量表示，其中第 $i$ 位为1表示第 $i$ 个记录当前字段取第 $t$ 个值；0表示不取该值。
例如一文件包括两个字段 $A, B$ ，分别取值范围为 $A=\{1,2,3\}$ ， $B=\{a,b,c\}$ 。一共有6个记录，分别是 $(2, c), (3, c), (2, a), (3, b), (1, b), (2, a)$ 。于是字段 $A$ 的位图索引为：

字段A取值	向量
1	000010
2	101001
3	010100

可发现当所有取值对应的向量做按位或运算后将变成全1向量，其表示的含义是当前字段 $A$ 取任意值，而任意几个取值对应的向量按位或，就代表对字段 $A$ 的范围查找。例如查找 $A$ 取值在2-3之间的所有记录，则可以直接将向量101001和010100按位或运算，得到111101，即满足的记录的编号有1、2、3、4、6。
若多个键联合查询，则对应每个字段满足条件的值对应的向量按位或运算，不同键之间根据逻辑进行运算，例如查询 $\textbf{and} B=b$ ，则分别对A和B字段按位或，得到的两个向量按位与运算，若查询 $\textbf{or} B!=b$ ，则对A按位或，对除B=b外按位或，得到的两个向量再按位或。因此可发现位图索引可以满足多关键字范围查找，仅需要向量的按位或或按位与运算。